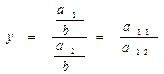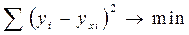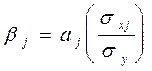Методы сводки и группировки аналитических данных

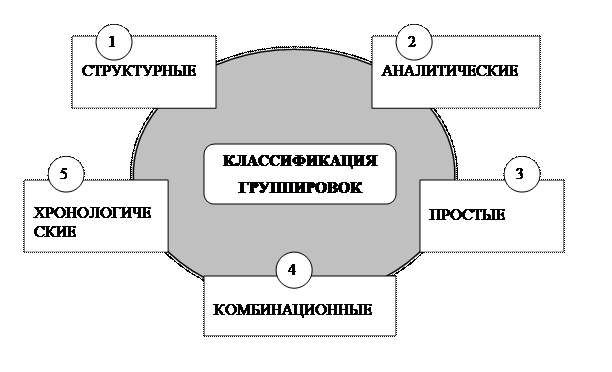
Сводка и группировка - важные элементы экономического анализа. Путем сводки можно подвести общий результат действия различных факторов на выпуск продукции, снижение себестоимости, повышение рентабельности и т.д.

Группировкой называют выделение среди изучаемых явлений характерных групп и подгрупп по тем или иным признакам. Группировки - распределение изучаемой совокупности на группы и подгруппы. Обычно группировки служат дополнением к детальному анализу средних величин.

Группировка - неотъемлемая часть каждого экономического исследования, производится в виде таблиц. Она позволяет учитывать те или иные экономические явления в их взаимосвязи и взаимозависимости, выявить влияние существенных факторов, обнаружить закономерности и тенденции развития явлений. Группировка опирается на определенную классификацию (рис. 3.4):

1) структурные - используются для изучения состава самих предприятий (по производственной мощности, уровню механизации, производительности труда, организационно-правовой форме, масштабам деятельности и друб.признакам), а также структуры выпускаемой ими продукции (по видам и заданному ассортименту).

2) аналитические - предназначены для выявления взаимосвязи, взаимозависимости и взаимодействия между изучаемыми явлениями, объектами, показателями. Из двух изучаемых признаков один является факторным, другой - результативным, для каждого конкретного случая они могут меняться (факторный признак может быть результативным и наоборот).

3) простые - групповые таблицы строятся по одному признаку.

4) комбинационные - групповые таблицы строятся по нескольким признакам.

5) хронологические - явление изучается в зависимости от времени.

Итак, при помощи группировки определяется зависимость одного показателя (результативного) от другого (факторного).

 

Рисунок 3.4 – Основные формы группировок

4. Балансовые увязки (метод). В экономическом анализе используются различные балансовые сопоставления и увязки. На промышленном предприятии с помощью этого метода анализируются:

– использование рабочего времени,

– станочного парка и производственного оборудования,

– движение сырья, полуфабрикатов, готовой продукции,

– финансовое положение.

Например, сопоставляется товарный баланс для определения суммы реализации товарной продукции и анализа влияния различных факторов на эту продукцию; сопоставляется баланс влияния различных факторов на итоговые показатели хозяйственной деятельности. Формула товарного запаса такова:

N_{зап. н. п.} + N_пос. = N_реал. + N_выб. + N_{зап.к.п.},

где N_{зап.н.п .} - запас товаров на начало отчетного периода; N_пос. - поступление товаров; N_реал - реализация товаров; N_выб. - прочее выбытие товаров (естественная убыль, уценка и др.); N_{зап.к.п.} - запас товаров на конец отчетного периода.

Каждую из обозначенных выше величин можно представить как алгебраическую сумму всех остальных.. Запас товаров на начало отчетного периода:

N_{зап.н.п.} = N_реал + N_выб + N_зап.к.п - N_пос..

Поступление товаров:

N_пос.. = N_реал + N_выб + N_зап.к.п - N_{зап.н.п.}.

Реализация товаров:

N_реал = N_зап.н.п + N_пос - N_выб - N_зап.к.п

Прочее выбытие:

N_выб = N_{зап.н.п.} + N_пос. - N_реал - N_реал

Запас товаров на конец отчетного периода:

N_зап.к.п = N_зап.н.п + N_пос.. - N_реал - N_выб

Сам товарный баланс позволяет сделать важные аналитические выводы, особенно если он составляется не только в целом, но и по отдельным группам сырья, готовых изделий, товаров. Причем по одноименным изделиям его можно выразить и в натуральном измерении. Кроме того на основе товарного баланса и с применением метода цепных подстановок, выявляется направление влияния на искомый показатель каждого алгебраического слагаемого.

Отметим, что в экономическом анализе полезно использовать многие методы бухгалтерского учета и составления отчетности, например метод двойной записи, калькуляции себестоимости отдельных изделий, нормативный метод, метод отклонений и т.п.

В экономическом анализе графики являются не только средством иллюстрации хозяйственных процессов, но и методом изучения экономики, который, однако, слабо разработан. Значение графического метода в анализе повышается в связи с расширением сферы изучения экономики на предприятиях не только менеджерами, но и общественностью.

В экономике связь между экономическими явлениями и показателями находит свое количественное выражение. Например, чем выше производительность труда рабочих и чем их больше, тем больше выпуск продукции. Такую зависимость, когда изменение одних величин обусловливает изменение других, называют функциональной.

Связь между переменными можно выразить тремя способами: таблицей, формулой и графиком. Табличный способ задания функции состоит в том, что значения функции, отвечающие определенным значениям аргумента или аргументов, приводятся в виде таблиц. Способ выражения зависимости с помощью формулы (уравнения) называется аналитическим. Наконец, при графическом способе зависимость между показателями изображается при помощи диаграммы (графика). В экономическом анализе для изображения функции одного аргумента пользуются в основном прямоугольными координатами.

Специальные методы включают в себя экономико-математические методы анализа состояния хозяйственной деятельности.

Экономико-математические методы используются при решении экономических задач на основе математики и кибернетики (рис.3.5).

Все экономико-математические методы имеют единую цель - оценить экономические явления и процессы в фактически сложившихся условиях хозяйствования, а также улучшить эмпирически сложившиеся варианты хозяйствования, выявляя внутрихозяйственные потери от принятия неоптимальных управленческих решений.

Экономико-математические методы обеспечивают сокращение сроков проведения анализа, более полный охват влияния факторов на результаты коммерческой деятельности, замену приблизительных расчетов точными вычислениями. Экономико-математические методы принято разделять на:

 

Рисунок 3.5 – Основные виды экономико-математических методов

 

1) эконометрические, которые построены на синтезе математики, статистики, экономики. Основой этих методов являются экономико-математические модели (схематическое научно-абстрактное описание с помощью математических средств того или иного хозяйственного процесса или явления);

2) методы оптимизации расчетов, в основе которых лежит математическое программирование. Применяются для решения задач оптимизации производственно-хозяйственной деятельности. К методам математического программирования относятся линейное, нелинейное, дискретное;

3) методы экономической кибернетики, которые анализируют экономические явления и процессы как сложные системы с точки зрения законов и механизмов управления и движения информации в них;

4) методы исследования операции подразумевают разработку целенаправленных действий, качественную оценку полученных решений и выбор из них наилучшего. Наиболее распространены такие методы: теория игр - для принятия оптимальных решений в условиях конфликта нескольких сторон, имеющих различные интересы; теория массового обслуживания - исследует на основе теории вероятностей математические методы количественной оценки процессов массового обслуживания.Теория игр как раздел исследования операций - это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы.

5) математическое программирование – это основное средство решения задач по оптимизации производственно-хозяйственной деятельности.

Линейное программирование это наука о методах нахождения экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения. Методы линейного программирования применяются для решения задач оптимизации математических моделей различных экономических систем. Эти задачи имеют множество альтернативных вариантов решений и определенные ограничения. Общий вид задачи, которая решается с помощью методов линейного программирования:

1) Целевая функция - это параметр оптимизации, который характеризует степень достижения цели системы, выраженный линейной зависимостью

F (Xj) = C ₁ X ₁ + C ₂ X ₂ +...+ C_nX_n → max или min,

где Сj (j = 1, n). константы, характеризующие параметры системы, которые определяют степень влияния переменных на значение параметра оптимизации; Xj. переменные системы, значение которых можно изменять для оптимизации системы.

Пределы изменения переменных определяются внешними факторами и параметрами системы и отражаются системой ограничений.

2) Система ограничений - совокупность всех ограничений, выраженных линейными уравнениями и неравенствами, которые накладываются на переменные системы:

A ₁₁ X ₁ + A ₁₂ X ₂ + A ₁₃ X ₃ +...+ A ₁ nX_n = > < B ₁

A ₂₁ X ₁ + A ₂₂ X ₂ + A ₂₃ X ₃ +...+ A ₂ nX_n = > < B ₂

Am ₁ X ₁ + Am ₂ X ₂ + Am ₃ X ₃ +...+ Am_nX_n = > < Bm,

Xj = >0, j = 1, n,

где Aij, Bi (j = 1, n; i = 1, m). константы, характеризующие внешние

факторы и параметры системы.

3) Допустимый план решения задачи - совокупность значений переменных Xj, которые удовлетворяют систему неравенств.

4) Область определения задачи - совокупность всех допустимых планов задачи.

5) Оптимальный план - это такой допустимый план, при котором целевая функция достигает своего экстремального значения (максимума или минимума в зависимости от целей системы). Оптимальный план является решением задачи. Найти оптимальный план - значит решить задачу. Целью применения методов линейного программирования как раз и является нахождение оптимального плана.

Методы линейного программирования позволяют выбрать из множества альтернативных решений оптимальное, которое обеспечивает максимальное достижение цели системы. Основные типы задач, которые решаются с помощью методов линейного программирования:

• задачи оптимального распределения ресурсов;

• задачи определения оптимальных питательных рационов;

• транспортная задача.

6) методы моделирования в анализе опираются на модели. Модель - это условный образ объекта. Экономико-математическая модель представляет собой схематичное научно-абстрактное описание с помощью математических средств того или иного экономического явления или процесса. Модель конструируется субъектом исследования так, чтобы отразить характеристики объекта: свойства, взаимосвязи, структурные и функциональные параметры. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторным выражается с помощью математического уравнения.

В детерминированном факторном анализе используются следующие типы моделей:

1. аддитивные

2. мультипликативные

3. кратные

4. смешанные и др.

При проведении факторного анализа, построенные модели на основе факторов первого уровня, можно расширять, добавляя в модель факторы второго, третьего и последующих уровней.

Применительно к классу детерминированных факторных систем различают следующие основные приемы моделирования.

1. Метод удлинения факторной системы. Исходная факторная система у = а₁/а₂. Если а₁ представить в виде суммы отдельных слагаемых факторов6

а₁ = а₁₁+а₁₂+а₁₃+…+а_1n,

то у = а₁₁/а₂+а₁₂/а₂+…+а_1n/а₂ – конечная факторная система вида у= Sх_i.

2. Метод расширения факторной системы. Исходная факторная система у=а₁/а₂. Если и числитель, и знаменатель дроби “расширить” умножением на одно и то же число, то получим новую факторную систему:

т.е. мультипликативную модель вида у=Пх_i

3. Метод сокращения факторной системы. Исходная факторная система у=а₁/а₂. Если и числитель, и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему (при этом, естественно, должны быть соблюдены правила выделения факторов):

В данном случае имеем конечную факторную систему вида у=х₁/х₂.

Таким образом, сложный процесс формирования уровня изучаемого показателя хозяйственной деятельности может быть разложен различными приемами на его составляющие (факторы) и представлен в виде модели детерминированной факторной системы.

Процесс моделирования факторных систем очень сложный и ответственный момент в экономическом анализе. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.

Содержание моделирования составляют:

• конструирование модели на основе предварительного изучения

объекта и выделения его существенных характеристик;

• экспериментальный или теоретический анализ модели на основе предварительного изучения объекта и выделения его существенных характеристик;

• сопоставление результатов с данными об объекте;

• корректировка модели.

Задачи моделирования: изучение наличия, направления и интенсивности связи показателей; ранжировка и классификация факторов; выявление формы связи между показателями; сглаживание динамики изменения уровня показателей; сравнение структуры связи в разных совокупностях.

Процесс моделирования осуществляется по этапам:

1. Анализ теоретических закономерностей, свойственных изучаемому явлению, и эмпирических данных о его структуре (четкая формулировка конечной цели построения модели и определение критерия, по которому будут сравниваться различные варианты). На этом этапе важно четко сформулировать цель построения модели и выбрать критерий сравнения вариантов решения.

2. Определение методов, с помощью которых можно решить задачу на основе построенной модели. Здесь важен выбор рационального метода.

3. Расчет и анализ полученных результатов. Критерием достоверности и качества модели на этом этапе является соответствие результатов исследования производственным условиям.

Различают следующие формы моделирования хозяйственных процессов:

- детерминированное которое можно свести к построению аддитивных моделей, мультипликативных и кратных;

- построение тождественного преобразования для исходной формулы экономического показателя по теоретически предлагаемым прямым связям последнего с другими показателями;

- стохастическое, обобщение закономерностей варьирования значений экономических показателей.

Экономико-математические методы и модели, основываясь на теории познания, обеспечивают практическую полезность хозяйственной деятельности, позволяют рационально обосновывать не только текущую деятельность, но и ближайшую перспективу развития субъекта хозяйствования.

Экономико-статистические методы - используются при изучении массовых повторяющихся экономических явлений, когда связь между анализируемыми показателями стохастическая (вероятностная). Наиболее распространены методы корреляции и регрессионный анализ. В процессе корреляционно-регрессионного анализа рассчитывается ряд основных параметров.

Корреляционно-регрессионный анализ является одним из наиболее распространенных математических методов, используемых в анализе хозяйственной деятельности предприятия. Применение этого метода требует использования программ решения задач на ЭВМ, так как корреляционно-регрессионный анализ требует большого количества трудоемких расчетов и большой подготовительной работы. Корреляционно-регрессионный анализ применяется в тех случаях, когда между анализируемыми показателями нет строгой зависимости и полного соответствия, тыс.е. нет функциональной зависимости. Корреляционный анализ основывается на массовости (не меньше 20 пар наблюдений) данных, так как малое количество наблюдений не позволяет обнаружить закономерность связи. Благодаря корреляционному анализу можно решить две задачи:

- Изучается теснота связи между исследуемыми показателями.

- Количественно измеряется степень влияния анализируемого фактора на исследуемый показатель, тыс.е. проявляется характер связи.

Параметры уравнения определяются с помощью метода наименьших квадратов:

Для проверки типичности найденных параметров используется критерий Стьюдента

 

Если t_а0> t_табл. < t_а1, то параметры признаются типичными.

 

Теснота связи между двумя показателями измеряется путем определения специального коэффициента корреляции (при прямой зависимости) или корреляционного отношения (при криволинейной зависимости). (табл. 3.1)

Для оценки значимости коэффициента корреляции используют критерий Фишера

 

m – число параметров уравнения

n – количество наблюдений

Если F_r > F_табл. величина коэффициента корреляции признается существенной.

Таблица 3.1 – Конечные результаты корреляционно-регрессионного анализа

Параметр	Характеристика	Оптимальное значение
Объем выборки	Количество данных по фактору. Используется для установления тенденций изменения фактора	Не менее чем в 3-5 раз больше количества факторов
Коэффициент вариации	Уровень отклонений значений факторов от средней анализируемой совокупности	Менее 33%
Коэффициент парной корреляции	Характеризует тесноту связи между i-м фактором и функцией.	Больше 0,1
Коэффициент множественной корреляции	Характеризует тесноту связи одновременно между всеми факторами и функцией. Применяется для выбора модели.	Больше 0,7
Коэффициент множественной детерминации	Характеризует степень влияния на функцию включенных в модель факторов. Равен квадрату коэффициента множественной корреляции	Больше 0,5
Критерий Фишера	Характеризует значимость уравнения регрессии	Значение выше табличного
Критерий Стьюдента	Характеризует существенность факторов, включенных в модель. Применим для выбора модели	Больше 2 (при вероятности 0,95)
Среднеквадратическая ошибка	Характеризует точность полученных коэффициентов регрессии. Применяется их для оценки	В <2 раза соответствующего коэффициента регрессии

 

Исследование взаимосвязи между тремя и более признаками осуществляется с помощью множественного корреляционно-регрессионного анализа, где также проводится выбор адекватной модели зависимости и тесноты связи. Для того, чтобы выявить какой фактор как влияет на результативный признак, применяют нормированные коэффициенты регрессии

a_j - коэффициент регрессии при х_j факторе

s_xj - среднее квадратическое отклонение факторного признака

s_y - среднее квадратическое отклонение результативного признака

Расчет частных коэффициентов эластичности позволяет определить на сколько процентов изменяется результативный признак при изменении факторного признака на один процент.

Проверка адекватности моделей построенных на основе уравнений регрессии производится по каждому параметру раздельно с помощью t-критерия Стьюдента

k – количество факторов в уравнении регрессии

Для трехфакторной модели коэффициент корреляции определяется по формyле

Проверка его значимости проводится с помощью F-критерия Фишера

Если F > F_табл., его значимость признается существенной.

Следует помнить, то применение корреляционной зависимости оправдано только в большой массе наблюдений, подчиняющихся закону нормального распределения.