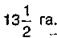Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Текстовая задача и процесс ее решения
План
1. Понятие «текстовая задача». Структура задачи. 2. Классификация задач. 3. Методы решения задач. 4. Этапы решения задачи. 5. Моделирование в процессе решения текстовых задач. 1. С термином «задача» люди постоянно сталкиваются в повседневной жизни как на бытовом, так и на профессиональном уровне. Каждому из нас приходится решать те или иные проблемы, которые зачастую мы называем задачами. Это могут быть общегосударственные задачи (освоение космоса, воспитание подрастающего поколения, оборона страны и т. п.), задачи определенных коллективов и групп (сооружение объектов, выпуск литературы, установление связей и зависимостей и др.), а также задачи, которые стоят перед отдельными личностями. Проблема решения и чисто математических задач, и задач, возникающих перед человеком в процессе его производственной или бытовой деятельности, изучается издавна, однако до настоящего времени нет общепринятой трактовки самого понятия «задача». В шиpoком смысле слова под задачей понимается некоторая ситуация, требующая исследования и разрешения человеком (или решающей системой). Отдельно стоят математические задачи, решение которых достигается специальными математическими средствами и методами. Среди них выделяют задачи научные (например, теорема Ферма, проблема Гольбаха и др.), решение которых способствует развитию математики и ее приложений, и задачи учебные, которые служат для формирования необходимых математических знаний, умений и навыков у разных групп обучаемых (школьников, слушателей курсов, студентов и др.) и направлены на изменение качеств личности обучаемого (не знал – знаю, не умел – умею и т. п.). Учебные математические задачи различаются по характеру их объектов. В одних задачах все объекты математические (числа, геометрические фигуры, функции и т. п.), в других объектами являются реальные предметы (люди, животные, автотранспортные и механические средства, сплавы, жидкости и т.д.) или их свойства и характеристики (количество, возраст, скорость, производительность, длина, масса и т. п.). Задачи, все объекты которых математические (доказательства теорем, вычислительные упражнения, установление признаков изучаемого математического понятия и т. д.), часто называют математическими заданиями.
Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т. д.). Перечисленные названия берут начало от способа записи (задача представлена в виде текста), сюжета (описываются реальные объекты, явления, события), характера математических выкладок (устанавливаются количественные отношения между значениями некоторых величин, связанные чаще всего с вычислениями). В последнее время наиболее распространенным является термин «текстовая задача». Текстовой задачей будем называть описание некоторой ситуации (явления, процесса) на естественном и (или) математическом языке с требованием либо дать количественную характеристику какого-то компонента этой ситуации (определить числовое значение некоторой величины по известным числовым значениям других величин и зависимостям между ними), либо установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения, либо найти последовательность требуемых действий. Придерживаясь современной терминологии, можно сказать, что текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т. п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь его количественные и функциональные характеристики. Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.
а) числовые значения величин, которые называются данными, или известными (их должно быть не меньше двух); б) некоторую систему функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой (словесный материал, указывающий на характер связей между данными и искомыми); в) требование или вопрос, на который надо найти ответ. Числовые значения величин и существующие между ними зависимости, то есть количественные и качественные характеристики объектов задачи и отношений между ними, называют условием (или условиями) задачи. В задаче обычно не одно, а несколько условий, которые называют элементарными.
Требования могут быть сформулированы как в вопросительной, так и в повествовательной форме, их также может быть несколько. Величину, значение которой требуется найти, называют искомой величиной, а числовые значения искомых величин – искомыми, или неизвестными. Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Для того чтобы уяснить структуру задачи, надо выявить ее условия и требования, то есть построить высказывательную модель задачи. Ответ на требование задачи получается в результате ее решения. Решить задачу в широком смысле этого слова – это значит раскрыть связи между данными, заданными условием задачи, и искомыми величинами, определить последовательность применения общих положений математики (правил, законов, формул и т. п.), выполнить действия над данными задачи, используя общие положения, и получить ответ на требование задачи или доказать невозможность его выполнения. Термин «решение задачи» широко применяется в математике. Этим термином обозначают связанные между собой, но все же неодинаковые понятия: 1) решением задачи называют результат, то есть ответ на требование задачи; 2)решением задачи называют процесс нахождения этого результата, то есть вся деятельность человека, решающего задачу, с момента начала чтения задачи до окончания решения; 3) решением задачи называют лишь те действия, которые производят над условиями и их следствиями на основе общих положений математики для получения ответа задачи. В дальнейшем мы не будем придерживаться какого-то одного значения этого термина и не станем пояснять, что мы имеем в виду в той или иной ситуации. В каждом конкретном случае будет ясно, о каком толковании термина «решение задачи» идет речь.
2. В зависимости от целей классификации выбирают основание для ее проведения и на его основе получают те или иные группы текстовых задач, которые объединяет либо метод решения, либо количество действий, которые необходимо выполнить для решения задачи, либо схожий сюжет и т. п. В зависимости от выбранного основания задачи можно классифицировать (то есть разделить на группы по выбранному основанию): – по числу действий, которые необходимо выполнить для решения задачи; – по соответствию числа данных и искомых; – по фабуле задачи; – по способам решения и др. Положив в основание классификации число действий, которые необходимо выполнить для решения задачи, выделяют простые и составные задачи. Задачу, для решения которой нужно выполнить одно арифметическое действие, называют простой. Задачу, для решения которой нужно выполнить два или большее число действий, называют составной. Выбрав в качестве основания классификации соответствие числа данных и искомых задачи, выделяют задачи определенные, задачи с альтернативным условием, неопределенные и переопределенные задачи. Чаще всего в задачах число условий (зависимостей между величинами) соответствует числу данных и искомых. Но встречаются задачи, в которых этого соответствия нет. Определенные задачи – это задачи, в которых условий столько, сколько необходимо и достаточно для получения ответа.
Неопределенные задачи – задачи, в которых условий недостаточно для получения ответа. Переопределенные задачи – задачи, имеющие условия, которые не используются при их решении выбранным способом. Такие условия называют лишними. Следует иметь в виду, что при решении задачи другим способом лишними могут оказаться уже другие условия. Если в переопределенной задаче лишние условия не противоречат остальным условиям, то она имеет решение. В начальном курсе математики неопределенные задачи называют задачами с недостающими данными, а переопределенные – задачами с избыточными данными. Положив в основание классификации фабулу задачи, чаще всего выделяют такие группы задач: «на движение», «на работу», «на смеси и сплавы», «на смешение и концентрацию», «на проценты», «на части», «на время», «на покупку и продажу» и т. п. Классифицировать задачи, исходя из фабулы условия, очень сложно, так как тематика условий задач бывает порой очень разнообразной. Множество задач, в которых имеется одинаковая зависимость между величинами, входящими в эти задачи, при возможном различии их числовых данных и фабул образуют определенный вид задач. Задачи одного вида имеют одну и ту же алгебраическую модель. Положив в основание классификации способы решения задач, можно выделить такие группы задач: 1) задачи на тройное правило; 2) задачи на нахождение неизвестных по результатам действий; 3) задачи на пропорциональное деление; 4) задачи на исключение одного из неизвестных; 5) задачи на среднее арифметическое; 6) задачи на проценты и части; 7) задачи, решаемые с конца, или «обратным ходом», и т. д. При решении задач различными методами используют, как правило, «свою» классификацию задач. Так, при алгебраическом методе решения чаще всего в качестве основания классификации берут фабулу задачи, а при решении арифметическим методом задачи классифицируют по способам их решения. Однако следует отметить, что такое разбиение задач на группы, строго говоря, не является классификацией, так как в этих случаях, с одной стороны, появляются задачи, которые не могут быть отнесены ни к одной из образовавшихся групп, с другой стороны, существуют задачи, которые могут быть отнесены к нескольким указанным группам. Вместе с тем, с точки зрения учебных целей, эти и подобные им «классификации» задач удобны. Они дают возможность выделить наиболее типичные виды задач и усвоить стандартные способы их решения.
3. Существуют различные методы решения текстовых задач: арифметический, алгебраический, геометрический, логический, практический и др. В основе каждого метода лежат различные виды математических моделей. Например, при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом – строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма. Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод – построив разные алгоритмы. Ясно, что и в этих случаях мы также имеем дело с различными методами решения конкретной задачи, которые (с целью избежать разночтения и неоднозначность трактовки термина «метод решения») будем называть способами решения. Иногда для краткости изложения вместо того, чтобы говорить, что задача решена определенным способом в рамках, например, арифметического метода, будем говорить, что «задача решена арифметическим способом» или «задача решена арифметическим методом», а то и просто – «задача решена арифметически». Арифметический метод. Решить задачу арифметическим методом – значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту же задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей. Алгебраический метод. Решить задачу алгебраическим методом – это значит найти ответ на требование задачи, составив и решив уравнение или систему уравнений (или неравенств). Одну и ту же задачу можно также решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми. Геометрический метод. Решить задачу геометрическим методом – значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур. Одну и ту же задачу можно также решить различными геометрическими способами. Задача считается решенной различными способами, если для ее решения используются различные построения или свойства фигур. Логический метод. Решить задачу логическим методом – это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения. Примерами таких задач могут служить задачи «на переправы», классическим представителем которых является задача о волке, козе и капусте, или задачи «на взвешивание».
Практический метод. Решить задачу практическим методом – значит найти ответ на требование задачи, выполнив практические действия с предметами или их копиями (моделями, макетами и т. п.). Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический, алгебраический и арифметический; арифметический и практический и т. п. В этом случае считают, что задача решается комбинированным (смешанным) методом.
4. Деятельность по решению задачи включает следующие этапы независимо от выбранного метода решения: 1. Анализ содержания задачи. 2.Поиск пути решения задачи и составление плана ее решения. 3. Осуществление плана решения задачи. 4. Проверка решения задачи. Рассмотрим более подробно каждый этап решения задачи. 1. Анализ задачи. Основное назначение этапа – осмыслить ситуацию, отраженную в задаче; выделить условия и требования, назвать данные и искомые, выделить величины и зависимости между ними (явные и неявные). На этом этапе решения задачи можно использовать такие приемы: а) представление той жизненной ситуации, которая описана в задаче; б) постановка специальных вопросов и поиск ответов на них; в) «переформулировка» задачи; г) моделирование ситуации, описанной в задаче, с помощью реальных предметов, предметных или графических моделей и др. Первый прием – представление той жизненной ситуации, которая описана в задаче, – выполняется фактически при чтении или слушании задачи. Вместе с тем мысленное воспроизведение всех объектов задачи и связей между ними может проводиться и позже. Цель такого воспроизведения – выявление основных количественных и качественных характеристик ситуации, представленной в задаче. Второй прием – постановка специальных вопросов и поиск ответов на них – включает следующий «стандартный» набор вопросов, ответы на которые позволяют детально разобраться в содержании задачи: 1) О чем говорится в задаче? 2) Что известно в задаче? 3) Что требуется найти в задаче? 4) Что в задаче неизвестно? и др. Третий прием – переформулировка текста задачи – состоит в замене данного в задаче описания некоторой ситуации другим описанием, сохраняющим все отношения, связи, качественные характеристики, но более явно их выражающим. Вся лишняя, несущественная информация при этом отбрасывается, текст задачи преобразуется в форму, облегчающую поиск пути решения. В ходе переформулировки выделяются основные ситуации, о которых идет речь в задаче, при необходимости строится вспомогательная модель задачи: краткая запись условия, таблица, рисунок, чертеж, диаграмма и т. п. Моделирование ситуации, описанной в задаче, с помощью реальных предметов, предметных моделей или графических моделей является еще одним, четвертым, приемом анализа задачи. 2.Поиск пути решения задачи и составление плана ее решения Назначение этапа – завершить установление связей между данными и искомыми величинами и указать последовательность использования этих связей. Проведя анализ задачи, не всегда просто найти путь ее решения. Поиск пути решения задачи является довольно трудным процессом, для которого нет точного предписания. Укажем некоторые приемы, помогающие осуществлять этот этап. Одним из приемов поиска пути решения задачи является анализ задачи по тексту или по ее вспомогательной модели. Поиск пути решения задачи можно осуществлять от вопроса задачи к данным (аналитический путь) или от данных к вопросу (синтетический путь). В первом случае (аналитический путь) на основе анализа задачи необходимо уточнить, что требуется найти в задаче, и определить, что достаточно знать для ответа на этот вопрос. Для этого следует выяснить, какие из нужных данных есть в условии задачи. Если они (или одно из них) отсутствуют, надо определить, что нужно знать, чтобы найти недостающие данные (или одно недостающее данное), и т. д., пока для определения очередного неизвестного оба данных будут известны. Поиск пути решения заканчивается составлением плана решения задачи. Под планом решения будем понимать объяснение того, что узнаем, выполнив то или иное действие, и указание по порядку выполнения арифметических действий. Во втором случае (синтетический путь) решающий выделяет в тексте задачи два каких-либо данных и на основе связи между ними, установленной при анализе, определяет, какое неизвестное может быть найдено по этим данным и с помощью какого действия. Затем, считая полученное число данным, решающий опять выделяет два взаимосвязанных данных и определяет, какое неизвестное может быть найдено по ним и с помощью какого действия, и т. д., пока выполнение очередного действия не приведет к определению искомого. При решении задач анализ и синтез в рассуждениях, как правило, переплетаются. Осуществляя поиск пути решения задачи синтетически, анализ часто производят «про себя». В то же время, каким бы приемом мы ни вели поиск пути решения составной задачи, ее предварительный анализ (хотя бы подсознательный) неизбежен. Еще одним из приемов поиска пути решения задачи является разбиение задачи на смысловые части. Сущность этой работы заключается в том, чтобы научиться различать в данной задаче отдельные, менее сложные задачи, последовательное решение которых позволяет получить ответ на требование данной. 3. Осуществление плана решения задачи Назначение этапа – найти ответ на требование задачи. Немаловажную роль при решении задач играет запись найденного решения. Прежде всего остановимся на используемых сокращениях при записи действий с именованными числами. При записи именованных чисел, выраженных в метрических мерах, используются наименования, принятые в международной системе единиц СИ, например, «м» – метр, «км/ч» – километров в час. Названия таких мер, как квадратный метр, кубический метр, записываются «м2», «м3». Все названия метрических мер, употребляемых без чисел, выписываются полностью словами, например: «сколько гектаров земли...», а не «сколько га земли...». Принято названия метрических мер выписывать полностью и в случае буквенной символики, например, «а литров», «b метров» и т. д. Однако часто этого не делают, а используют более удобную запись «х км/ч», «у м3» и т. д. Что касается других наименований, то здесь нет общеустановленных условных обозначений. Вместе с тем в последнее время, как правило, вместо «руб.» принято писать «р.», вместо «коп.» – «к.» и др. При письменном решении используют три формы записи решения: 1) запись решения в виде отдельных действий (так называемое решение по действиям); 2) запись решения в виде выражения; 3) запись решения с объяснением. 1. Запись решения в виде отдельных действий. Запись решения в виде отдельных действий может осуществляться в трех вариантах. А. Без записи пояснений Пример. В двух поселках было 24 600 жителей. Когда население первого поселка увеличилось в Решение. Примем за единицу первоначальное число жителей первого поселка:
Ответ: в первом поселке – 14 350 жителей, во втором – 10 250 жителей. Б. С записью пояснений Пример. С двух участков земли общей площадью 8,5 га собрано всего 58 ц льноволокна. С каждого гектара первого участка собрано в среднем Определите площадь каждого участка. Решение.
5) 8,5 – 5 = 3,5 (га) – площадь первого участка. Ответ: 3,5 га; 5 га. В. С записью пояснений в вопросительной форме Пример. Переднее колесо экипажа на некотором расстоянии сделало на 120 оборотов больше заднего. Найдите это расстояние, если окружности колес экипажа соответственно равны 2 м и 3 м. Решение. Наименьшее расстояние, которое пройдет экипаж, а колеса сделают целое число оборотов, равно 6 м. Далее рассуждаем так. 1. Сколько оборотов сделает переднее колесо на расстоянии 6 м? 6: 2 = 3 (об.). 2. Сколько оборотов сделает заднее колесо на расстоянии 6 м? 6: 3 = 2 (об.). 3. На сколько больше оборотов сделает переднее колесо, чем заднее, на расстоянии 6 м? 3 – 2 = 1 (об.). 4. Во сколько раз больше оборотов сделает переднее колесо, чем заднее, на искомом расстоянии? 120: 1 = 120 (раз). 5. Чему равно расстояние? 6 – 120 = 720 (м). Ответ: 720 м. 2. Запись решения в виде выражения. В этом случае сначала записываются отдельные шаги в соответствии с планом, затем составляется выражение и находится его значение. Пример. Набор двух томов сочинения, содержавших каждый по 340 страниц, по 36 строк на странице и по 45 букв в строке, был поручен двум наборщикам – каждому по одному тому. Первый набирал по 900 букв в час и закончил работу на 153 ч. раньше своего напарника. Сколько букв в час набирал второй наборщик? Решение. 45 × 36 (б.) – число букв на странице; 45×36 × 340(6.) – число букв в книге; (45 × 36 × 340): 900 (ч) – работал первый наборщик; ((45 × 36 × 340): 900 + 153) (ч) – работал второй наборщик; (45 × 36 × 340): ((45 × 36 × 340): 900 + 153) = 720 (б.) – набирал в час второй наборщик. Ответ: второй наборщик набирал 720 букв в час. 3. Запись решения с объяснением. Эта запись решения встречается реже, чем две предыдущие. Пример. Найти шестизначное число по следующим условиям. Число оканчивается цифрой 2. Если эту цифру переставить с последнего места на первое, то получится число, втрое меньше искомого. Решение. По условию число, полученное при перестановке цифр, втрое меньше искомого. Значит, искомое число можно рассматривать как произведение некоторого шестизначного числа, у которого первая цифра 2, на число 3, то есть (2** ***) × 3 = *** **2. Искомое шестизначное число оканчивается цифрой 2. Цифра 2 могла получиться только в результате умножения 3 на 4, следовательно, в первом сомножителе цифра единиц равна 4. Так как по условию последнюю цифру 2 искомого числа переставили на первое место, то в искомом числе цифра 4 означает число десятков, то есть (2** **4) × 3 = *** *42. В состав 4 (цифры разряда десятков искомого числа) входит число 1, добавленное в число десятков после умножения 4 единиц на 3. Поэтому число десятков 4 – 1 = 3. Число 3 могло получиться от умножения на 3 только 1. Отсюда число сотен искомого числа равно 1, то есть (2** *14) × 3 = *** 142. В разряде сотен 1 могла получиться лишь от умножения 7 на 3. Значит, число тысяч искомого числа 7, то есть (2**714) × 3 = **7 142. В число тысяч входит число 2, добавленное в число тысяч от умножения семи сотен на 3. Следовательно, от умножения числа тысяч на 3 получается в произведении число, последняя цифра которого 5 (7 – 2 = 5). Число 5 может получиться лишь от умножения 5 на 3, значит, в искомом числе десятков тысяч пять, то есть (2*5 714) × 3 = *57 142. В состав 5 входит число 1, добавленное от умножения 3 на 5. Отсюда от умножения только десятков тысяч получилось произведение, оканчивающееся на 4 (5 – 1 = 4). Число 4 могло получиться от умножения на 3 только 8, следовательно, сотен тысяч всего восемь, то есть 285714-3 = 857 142. Итак, искомое число 857142, а получилось оно в результате умножения 285 714 на 3. Ответ: 857142. 4. Проверка решения задачи Назначение этапа – установить, правильно ли понята задача, и выяснить, не противоречит ли полученный ответ всем другим условиям задачи. Этот этап является обязательным при решении задач. Следует помнить, что логичные рассуждения на других этапах решения задачи не гарантируют правильности ее решения. Проверку решения задачи можно проводить различными способами. Перечислим их. I. Установление соответствия между числами, полученными в результате решения задачи и данными в условии задачи. II. Составление и решение задачи, обратной данной. III. Решение задачи различными способами. IV. Решение задачи различными методами. V. Прикидка (грубая проверка). Остановимся на каждом из них подробнее. I. Проверка решения задачи способом установления соответствия между числами, полученными в результате решения задачи, и данными в условии задачи заключается в следующем: числовые значения искомой величины, полученные в ответе на вопросы задачи, вводятся в текст задачи, и устанавливается, не возникают ли при этом противоречия, а затем выполняются арифметические действия с числовыми значениями величин, согласно их связям между собой, которые заданы в условии задачи. Если при этом получаются числа, данные в условии задачи, то делается заключение о верном ее решении. II. Проверка решения задачи способом составления и решения задачи, обратной данной, заключается в том, что после решения задачи составляется обратная по отношению к данной задача. Если при ее решении в ответе получится значение величины, которое было задано в условии данной задачи, то можно считать, что она решена правильно. Пример. Три маляра могут покрасить участок стены за 1,6 ч. За сколько времени мог бы выполнить эту работу один третий маляр, если известно, что один первый покрасил бы этот участок за 8 ч., а один второй – за 6 ч.? Решение. Примем всю работу за единицу. 1) 1: 8 = 1/8 (ч.) – работы выполняет первый маляр за 1 ч.; 2) 1: 6 = 1/6 (ч.) – работы выполняет второй маляр за 1 ч.; 3) 1: 1,6 = 5/8 (ч.) – работы выполняют три маляра за 1 ч.; 4) 1/8 + 1/6 = 7/24 (ч.) – работы выполняют первый и второй маляры за 1 ч.; 5) 5/8 – 7/24 = 1/3 (ч.) – работы выполнит третий маляр за 1 ч.; 6) 1: 1/3 = 3 (ч.) – за столько времени третий маляр выполнит работу. Для проверки составляем обратную задачу: «Три маляра могут покрасить участок стены за 1,6 ч. За сколько времени мог бы выполнить эту работу один первый маляр, если известно, что один второй покрасил бы этот участок за 6 ч., а один третий – за 3 ч.?» Решение 1) 1:6=1/6(4.); 4)1/6 + 1/3 = 1/2(4.); 2) 1: 3 = 1/3 (ч.); 5) 5/8 – 1/2 = 1/8 (ч.); 3) 1:1,6 = 5/8(4.); 6) 1: 1/8 = 8 (ч). Итак, получили число, которое было задано в условии исходной задачи. Ответ: за 3 ч. III. Проверить решение задачи можно, решив ее различными способами. Напомним, что задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей. Получив при решении задачи различными способами один и тот же результат, делают вывод о том, что задача решена верно. Пример. Фермер получил в аренду 40,5 га земли. Участок, равный Решение 1-й способ 1) 2) 3) 4) 5) 2-й способ 1) 2) 3) В каждом из предложенных способов решения получен один и тот же результат. Ответ: под кормовые травы отведено IV. Проверку решения задачи можно выполнить, решив задачу различными методами (арифметическим, алгебраическим, геометрическим и др.). В этом случае, получив один и тот же результат, делают вывод о том, что задача была решена верно. Пример. Из одного города в одном направлении вышли два поезда. Первый поезд шел со скоростью 60 км/ч., а второй – 90 км/ч. Второй поезд вышел на 2 ч. позже. Через сколько часов и на каком расстоянии от города второй поезд догонит первый? Решение Арифметический метод. Краткая запись задачи показана на рисунке 1. 1) 60 × 2 = 120 (км) – пройдет первый поезд за 2 ч.; 2) 90 –× 60 = 30 (км/ч) – на столько километров в час скорость второго поезда больше скорости первого;
Рис. 1
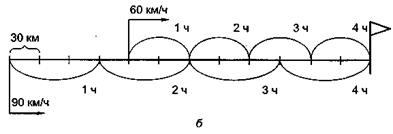
3) 120: 30 = 4 (ч.) – через столько часов после своего выхода второй поезд догонит первый; 4) 90 × 4 = 360 (км) – на таком расстоянии от города второй поезд догонит первый. Геометрический метод (конструктивный прием) 1-й способ. Примем условно длину одного отрезка по вертикали за 30 км, а длину одного отрезка по горизонтали – за 1 ч. Отложим на горизонтальной прямой время от 0 до 6 ч., по вертикали будем откладывать отрезки пути, пройденные каждым поездом за 1 ч., 2 ч., 3 ч. и т. д. (рис. 2, а). Сначала откладываем отрезки пути, пройденные первым поездом до выхода второго, а затем отрезки, характеризующие расстояния, пройденные первым поездом за 3 ч. и вторым за 1 ч., первым за 4 ч. и вторым за 2, первым за 5 ч. и вторым за 3 ч. и, наконец, первым за 6 ч. и вторым за 4 ч. Отрезки найденных путей оказались равными, значит, второй поезд догонит первый через 4 ч. после своего выхода или через 6 ч. после выхода первого. Как видно из рисунка, произойдет это на расстоянии 360 км от города.
Рис. 2 2-й способ. За 2 ч. первый поезд проходит 60 × 2 = 120 (км), значит, к началу движения второго поезда расстояние между поездами было 120 км. Примем условно длину одного отрезка по горизонтали за 30 км, и станем откладывать отрезки пути, пройденные каждым поездом за 1 ч. (рис. 2, б). Видим, что к концу четвертого часа после начала движения второго поезда на расстоянии 90 × 4 = 360 (км) от города второй поезд догонит первый. В каждом из предложенных методов решения получен один и тот же результат. Ответ: через 4 ч. после своего выхода на расстоянии 360 км от города второй поезд догонит первый. V. Проверка решения задачи прикидкой правильного ответа. Суть этого способа состоит в установлении границ для искомого числа. Он позволяет грубо оценить правильность решения задачи, и если в результате прикидки мы не выясним, что некоторые значения искомых не удовлетворяют условию задачи, то необходимо провести проверку каким-либо другим способом. Пример. Из одного пункта в одном направлении через каждые полчаса выезжает велосипедист. Первый едет со скоростью 10 км/ч, второй – 8 км/ч. Найти скорость третьего велосипедиста, если известно, что он обогнал первого велосипедиста на 4 ч. позже, чем второго. Решение. Пусть х км/ч – скорость третьего велосипедиста. При движении в одном направлении время встречи находится как отношение расстояния между объектами к разности их скоростей. Второй велосипедист за 0,5 ч проедет 8 км/ч × 0,5 ч = 4 км. Следовательно, третий его догонит (они встретятся) через 4/(х – 8) ч. Первый за 1 ч. проедет 10 км. Значит, третий его догонит (они встретятся) через 10/(х – 10) ч. По условию задачи Преобразовав это уравнение, получим: 10 х – 80 – 4 х + 40 = 4 х 2 – 72 х + 320 => 2 х2 – 39 х + 180 = 0. Решив квадратное уравнение, находим х 1 = 12, х 2= 7,5. Проверка. Прикидываем, что скорость третьего велосипедиста должна быть большей, чем скорости первого и второго велосипедистов (больше 10 км/ч), иначе он не сможет их догнать. Следовательно, второй корень не подходит. Ответ: скорость третьего велосипедиста – 12 км/ч. Обратим внимание на то, что прикидка не позволяет проверить правильность полученного числового значения ответа. В некоторых случаях она лишь позволяет определить, что задача решена неверно. В процессе решения задач необходимо проверять полученный ответ на требование задачи, выбрав наиболее рациональный способ, учитывающий специфику задачи. Например, задачу на встречное движение удобно проверять, решив ее различными способами, а задачу на нахождение неизвестных по двум разностям – способом установления соответствия между числами, полученными в результате решения задачи, и числами, данными в условии задачи. Следует помнить, что, выполняя проверку задачи любым из указанных способов, необходимо выяснить, не противоречит ли полученный ответ всем условиям задачи. На практике это означает, что при решении обратной задачи или при решении задачи другими методами логика рассуждений должна быть отличной от логики рассуждений, применяемой в ходе решения данной задачи. Несоблюдение этого может привести к тому, что ошибочное решение не будет обнаружено.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 16088; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.39.74 (0.135 с.) |
 В каждой задаче можно выделить:
В каждой задаче можно выделить: раза, а население второго поселка уменьшилось на
раза, а население второго поселка уменьшилось на  своего числа, в первом поселке оказалось в
своего числа, в первом поселке оказалось в  раза больше жителей, чем во втором. Определите первоначальное число жителей каждого поселка.
раза больше жителей, чем во втором. Определите первоначальное число жителей каждого поселка.





 ц, с каждого гектара второго участка – 5,6 ц.
ц, с каждого гектара второго участка – 5,6 ц. – предполагаемый сбор льноволокна;
– предполагаемый сбор льноволокна; – снижение сбора со всей площади за счет 2-го участка;
– снижение сбора со всей площади за счет 2-го участка; – настолько центнеров каждый гектар 2-гоучастка снижал сбор;
– настолько центнеров каждый гектар 2-гоучастка снижал сбор; – площадь второго участка;
– площадь второго участка; этой площади, засадили плодовыми деревьями, а
этой площади, засадили плодовыми деревьями, а  остальной площади отвели под кормовые травы. Какая площадь отведена под кормовые травы?
остальной площади отвели под кормовые травы. Какая площадь отведена под кормовые травы?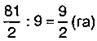 – составляет
– составляет 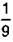 от
от  га;
га; – составляет
– составляет  от
от  га;
га; – 18 =
– 18 =  (га) – всей разработанной площади осталось после выделения участка под плодовые деревья;
(га) – всей разработанной площади осталось после выделения участка под плодовые деревья;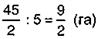 – составляет
– составляет 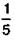 от
от  га;
га; – отведено под кормовые травы.
– отведено под кормовые травы. – всей разработанной площади осталось после выделения участка под плодовые деревья;
– всей разработанной площади осталось после выделения участка под плодовые деревья; – всей разработанной площади отведено под кормовые травы;
– всей разработанной площади отведено под кормовые травы; – отведено под кормовые травы.
– отведено под кормовые травы.