Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация алгоритмов эвристического поиска
Различают алгоритмы: 1. Поиск в глубину - использует эвристическую функцию вида F(n) = ^h(n). Это жадный алгоритмы, которые выбирают на каждом шаге наилучшее решение для продолжения. 2. Поиск в ширину (переборный) - работают с эвристической функцией вида F(n) = g(n) и ориентируются на совершенные затраты 3. Смешанный поиск - работают с эвристической функцией вида F(n) = a*
Нейронные сети Нейронные сети представляют собой упрощённую модель человеческого мозга. Мозг состоит из нейронов, которые рассматриваются как индивидуальные процессоры. Математическая модель поведения клетки мозга создали Макколок и Питс.
Коэффициенты ai задаются в процессе обучения, или путем решения системы уравнений. Если y > 0, то считается что нейрон распознал образец. На практике нейроны обычно объединяют в сеть.
Xi – соответствует ключевым словам (если xi = 1, то слово присутствует в запросе) Для вычисления коэффициентов ai используют формулы sqrt((xi - xэ)2) -> min: (xi - xэ)2 -> min xi2 – 2xi*xэ + xэ2 - > min 2xi*xэ – xэ2 -> max 2xэ1*x1 + 2xэ2*x2 + … + 2xэn*xn – xэ12 – xэ22 - … - xэn2 -> max 2xэi === ai
Для нейрона с линейной функцией распознавания процедура обучения такова: На вход нейрона подаются объекты для которых известно, относятся они к данной теме или нет. Если нейрон распознает верно, то никакая корректировка коэффициентов не выполняется. Ошибочная реакция нейрона может состоять в следующем: Нейрон отклонил образец – ai = ai гамма * xi нейрон принял неправильный образец и не распознал его ai = ai гамма * xi гамма – обычно = 1, чем меньше, тем выше точность и ниже скорость обучения. Такой способ обучения сойдется с результатом если обучающая выборка нейрона принципиально отделима на основе линейной функции 1, что проиллюстрировано на рисунке:
Переменные a – t задают ключевые слова. Пусть нейрон распознает класс W1, пусть эталонный документ класса xэ =< 111110000000 2a+2b+2c+2d+2e+0f + 0g+0h+0j+0k+0q+0t – 5. Согласно общей концепции значение этой функции на объектах внутри этого класса должно быть больше нуля, а вне этого класса меньше 0. Для документа D4 правило не сработало (значение распознающей функции < 0, хотя D4 принадлежит W1) Корректируем D4 <101000001000> = 3a+2b+3c +2d + 2e+ 1j – 5 Теперь все образцы обучающей таблицы распознаются верно, так что было достаточно только одной коррекции. Теорема Колмогорова-Габора: Любую непрерывную дифференцируемую функцию можно аппроксимировать (приближенно описать) на заданном конечном интервале полиномом подходящей степени сколь угодно точно.
Более точную аппроксимацию дает кривая вида Полином второй степени от двух кривых в общем виде: P(x1, x2) = C1x12 + C2x22 + C3X1X2+ C4x1 + C5X2 (4) Полином третьей степени P(x1, x2) = C1x13 + C2x23 + C2x23+ C3X1X2+ C4x1 + C5X2 (4) …??? Для отыскания коэффициентов полинома второй, третьей.. n-ой степеней, можно использовать тот же метод что и бля полинома первой степени.. Рассмотрим пример: Рассмотрим полином второй степени. Пусть обучающая выборка представлена таблицей
Допустим, что линейную функцию для этой таблице нельзя, тогда расширимэту таблицу членами второго порядка, получим таблицу:
Теперь можно построить линейную функцию вида y = a1x1 +a2x2+a3+z1 +a4z2+a5+z3, z1 = x12, z2 = x22, z3 = x1x2. Теорема Колмогорова-Габора гарантирует, что при весьма общих условиях требуемый полином все построить удастся.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 163; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.24 (0.01 с.) |
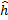 (n+ (1-a)*g(n). 0 <=a <= 1. Следует найти a. Считается что на ранних этапах следует брать a = 0, а на поздних полагают a = 1, т.е. переводят на жадный вариант поиска.
(n+ (1-a)*g(n). 0 <=a <= 1. Следует найти a. Считается что на ранних этапах следует брать a = 0, а на поздних полагают a = 1, т.е. переводят на жадный вариант поиска.