
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аксиоматические теории. Непротиворечивость.Стр 1 из 6Следующая ⇒
Вопросы к экзамену 1. +Множества. Отношения. Примеры. 2. +Математические структуры. Примеры. 3. +Модели. Примеры. 4. +Изоморфизм. 5. +Аксиоматические теории. Непротиворечивость. 6. +-Независимость аксиом. 7. +-Полнота. Роль теории множеств. 8. +Аксиоматика Вейля. 9. +Непротиворечивость аксиоматики Вейля. 10. +Простейшие следствия аксиоматики Вейля. 11. + Аксиоматика Гильберта. I и II группы. 12. + Аксиоматика Гильберта. III, IV, V группы. 13. +Аксиоматика Погорелова. 14. +Непротиворечивости аксиоматики Погорелова. 15. +Геометрия Лобачевского. 16. + Модель Клейна. 17. + Непротиворечивость геометрии Лобачевского. 18. +Модель Пуанкаре. Множества и отношения. Примеры. Если X- мн-ва,то
P(x)-мн-ва всех подмножеств Х. Отношение Примеры 1. n=1 2. n=2 бинарное отношение. 1) E – мн-во точек евклидовой плоскости, L – мн-во всех прямых.
2) S – мн-во всех треугольников на плоскости или прстранстве. Среди бинарных отношений выделяются отношения «эквивалентности» которые удовлетворяют 3 свойствам: рефлексивность, симметричность, транзитивность. 3. n=3 тенарное отношение E -мн-во точек пространства евклида.
4. Отображение (ф-ция) х,у - множества f: х -> у х->f(х)=у
5. Алгебраические операции определяются через отоброжения и поэтому также явл. отношением.
f: 6. Скалярное произведение G: 7. Меорина M – пространство точек
8. Откладывание вектора E - пространство точек
Математические структуры. Примеры Основным методом в современной математике является аксиоматиче- ский метод в теоретико-множественном понимании, тесно связанный с поня- тием математической структуры. Пусть А1,А2,А3,...,Аn - непустые множества. А1 ЧА2 ЧА3 Ч...ЧАn - прямое (декартово) произведение этих множеств, т.е. множество всех упоря- доченных n-местных кортежей (a1;a2;...;an), элемент ai которых, стоящий на i-ом месте, принадлежит множеству Ai,i =1,2,...,n. В теоретико-множественной записи: А1ЧА2 ЧА3 Ч...ЧА ={(a1,a2,...,an)|ai∈Ai}. n Определение 1.1.1. Любое подмножество декартова произведения множеств
А1 ЧА2 ЧА3 Ч...ЧА называется n-арным (или n-местным) отношением δ, nопределенным во множествах А1,А2,А3,...,Аn. Замечание. Из определения имеем: 1) δ ⊂А1ЧА2 ЧА3 Ч...ЧАn. 2) Элементы (a1;a2;...;an)(ai∈Ai,i =1,2,...,n) находятся в отношении δ,ес- ли (a1;a2;...;an)∈δ. 3) Если А1 = А2 = А3 =...= Аn = A, то А1 ЧА2 ЧА3 Ч...ЧАn = An - n-аядекар- това степень множества A. 4) Если δ ⊂An, то говорят: на множестве A определено n-арное отношение δ. 5) В случае бинарного отношения δ ⊂A1 ЧA2 вместо (a1;a2)∈δ пишут a1δa2 - «a1 находится в отношении δ с a2». Например, отношение равенства на множестве R всех вещественных чисел – бинарное отношение. 6) Пусть на множестве A определена алгебраическая операция (внутренний закон композиции) ϕ: AЧA→A. Ее можно рассматривать как тернарное отношение δ ⊂AЧAЧA= A3, где δ ={(a,b,c)∈A3 |ϕ(a,b) = c}, a,b,c∈A. 7) Пусть на множестве A определен внешний закон композиции f с множе- ством операторов Λ: f:ΛЧA→A. Его можно рассматривать как тернарное отношение, определенное на множе- ствах Λ,A при помощи подмножества δ ⊂ΛЧAЧA, т.е. δ ={(λ,a,b)∈ΛЧAЧA| f (λ,a)=b}, λ∈Λ, a,b∈A. Рассмотрим конечную систему различных непустых множеств А1,А2,А3,...,Аn. Пусть, например, n= 3. 7 Пусть σ ={δ1,δ2,...,δk} - некоторая система тернарных отношений, оп- ределенных на множествах А1,А2,А3 и обладающих свойствами α1,α2,...,αt. То есть δi - это такое подмножество декартова произведения А1ЧА2ЧА3, которое обладает всеми свойствами α1,α2,...,αt одновременно. Может быть, что существует не одна, а несколько таких систем отно- шений σ ={δ1,δ2,...,δk}. Например, ϕ - алгебраическая операция на множе- стве R действительных чисел: ϕ:RЧR→R (т.е. ϕ можно рассматривать как единственное отношение δ ={(a,b,c)∈R3 |ϕ(a,b)=c}, a,b,c∈R). Пусть отношение δ обладает свойством коммутативности α1:ϕ(a,b)=ϕ(b,a)∀a,b∈R. Можно указать два знчения отношения δ, обладающего свойством α1 (т.е. две коммутативные операции на R): δ′ - сложение, δ′′- умножение, т.е. δ′ ={(a,b,c)∈R3 |a+b=c}, δ′′ ={(a,b,c)∈R3 |a⋅b=c}.
Пусть Τ - непустое множество всех систем σ ={δ1,δ2,...,δk} отноше- ний, каждое из которых обладает заданными свойствами α1,α2,...,αt. Определение 1.1.2. Элемент σ∈Τ определяет на множествах А1,А2,А3 математическую структуру рода Τ. Определение 1.1.3. Явно сформулированные свойства α1,α2,...,αt, оп- ределяющие множество Τ, называются аксиомами структуры рода Τ. Определение 1.1.4. Множества А1,А2,А3 называются базой структуры рода Τ. Таким образом, математическая структура рода Т представляет со- бой одно или несколько множеств А1,А2,А3,...,Аn(образующих базу струк- туры), элементы которых произвольной природы (основные, неопределяемые понятия данной теории) и находятся в некоторых отношениях δ1,δ2,...,δ (называемых основными неопределяемыми отношениями), удов- летворяющих аксиомам α1,α2,...,αt. Аксиомы иногда характеризуют не одну с точностью до изоморфизма, а некоторое множество математических структур. Совокупность всех струк- тур, определенных данной системой аксиом Σ ={α1,...,αt}, называется родом Т этих структур. Совокупность предложений, которые можно вывести логическимпу- тем из аксиом структуры, называется теорией структуры рода Т. В 30-х годах ХХ в. Н. Бурбаки определил математику как науку о ма- тематических структурах. Математические структуры подразделены им на три вида: алгебраические, порядковые и топологические. Евклидово, псевдо- евклидово, риманово, псевдориманово пространства, пространственно- временной континуум являются примерами структур топологического типа. 8 Рассмотрим простейшие структуры алгебраического типа. Всем струк- турам одного и того же рода дают специальное название: структура группы, структура n-мерного векторного пространства и др. Пример 1.1.1. (структура группы). Система σ ={δ1,δ2,...,δk} отноше- ний состоит из одного тернарного отношения δ ⊂GЧGЧG=G3, соответст- вующего алгебраической операции: ϕ:GЧG→G (т.е. ϕ можно рассматривать как единственное отношение δ ={(a,b,c)∈G3 |ϕ(a,b)=c}, a,b,c∈G). База состоит из одного множества G. Три аксиомы системы аксиом Σ ={α1,α2,α3} структуры группы: α: ∀a,b,c∈G:ϕ(ϕ(a,b),c)=ϕ(a,ϕ(b,c)) - аксиома ассоциативности; α2:∃e∈G∀a∈Gϕ(a,e)=ϕ(e,a)=a - существование нейтрального элемен- та; α3:∀a∈G∃a′∈G ϕ(a,a′)=ϕ(a′,a)=e - существование симметричного элемента. Пример1.1.2. (структура n-мерного векторного пространства над заданным полем). База состоит из двух множеств – основного множества V (его элементы - векторы – основные неопределяемые понятия); вспомогательного множест- ва K(его элементы условно называются скалярами). Система отношений σ ={δ1,δ2,...,δk} состоит из двух тернарных отношений: δ1 ⊂KЧVЧV, δ1 ={a, xr, yr | f (a, xr)= yr}, a∈K, xr, yr∈V; δ2 ⊂V ЧVЧV =V3, δ2 ={(ar,br,cr)|ϕ(ar,br) = cr}, ar,br,cr∈V. Аксиомы структуры векторного пространства V над полем K: α1:∀λ,μ∈K∀ar∈V f (λ, f (μ,ar)= f (λμ,ar); α2:∀λ,μ∈K∀ar∈V f (λ+μ,ar)=ϕ(f (λ,ar), f (μ,ar)); α3:∀ar∈V f (1,ar)=ar; α ∀r r∈∀λ∈ λ ϕ r r =ϕ λ r λ r; 4:a,b V, K f (, (a,b)) (f (,a), f (,b)) α5:∃0r∈V ∀ar∈Vϕ(0r,ar) =ϕ(ar,0r) = ar; α∀ar∈V∃ −ar∈V ϕar −ar =ϕ −arar = r; 6: () (,()) ((),) 0
α7:ϕ(ar,br)=ϕ(br,ar)∀ar,br∈V; α8:ϕ(ar,ϕ(br,cr))=ϕ(ϕ(ar,br),cr)∀ar,br,cr∈V. Таким образом, теория структур рода Т – это множество предложе- ний (теорем), являющихся логическими следствиями аксиом структуры рода Τ. Предметом математики являются математические структуры. Основ- ной метод математики – дедуктивный аксиоматический (от общих акси- ом к частным следствиям из них): - вводятся неопределяемые, первичные понятия структуры; - вводятся основные отношения; - структуры строятся с помощью аксиом; - затем, используя законы логики, строится теория структур данного рода. Модели. Примеры. Модели(интерпретации)если даны 2 аксиоматические теории S(«старая»), T(«новая»),то построить модели теории T на основе S означает следующее: 1)первоначальное понятие Т определяется на основе S 2) «первоначальное отношение Т» определяется на основе S 3) аксиомы ξ(кси)S=> ξT Другими словами аксиоматика Т док-ся как теоремы в теории S Если построена модель теории Т на основе S,то можно сказать,что теория Т как бы вкладывается в теорию S Примеры 1) геометрическая модель векторного пр-ва. Двумерное в-рное пр-во к аксиомам 1-8 добавл 9.dimv=2, 1-9 описывает теорию Т двумерного в-рного пр-ва. S- евклидовагеомпл-сть. Векторы опред-ся как направл отрезки 2) арифметич модель двумерного в-рного пр-ва V=R2={(a1,a2)(ai?R)} мн-во всех упорядоченных пар чисел а =(а1,а2), а+в=(а1+в1,а2+в2), к*а=(к*а1,к*а2) а+в=(а1а2+в 1в2)=(а1+в1,а2+в2)=(в1+а1,в2+а2)=(в1,в2)+(а1,а2) Изоморфизм. Примеры Если 2 структуры 1 рода, те у них однотипные понятия и одинаковое число однотипных отношений и мдмнож-ми понятий соотв. Можно установить взаимнооднознсоотв так, что эти соотв (отображения)сохр отношение. Примеры! 1) G=<R+ *,°>; H=<R,(+)> G->H:X->lnx; F(x)=Lnx; F(xy)=f(x)+f(y); ln(xy=lnx+lny) 2) (M1,p1(po)) метрическое простран-во; p1:M1xM1->R+; (M2p2)- еще одно метрич про-во. Изоморфизм в этом случае наз изометрия f:M1->M2 взаимнооднозначноеотобр (x,y)?M1; p1(x,y)=p2(f(x1)+f(x2) 3) Если vпроиз вектора про-во. вводится понятие линейной зависимости, независимости, базиса и координат и размерность, затем док-ся что произв векторное про-во размерности dimv=n изоморфно Rn={a1..an|ai?R} если v над R изоморф структуры астр и более конкр модели Аксиоматика Вейля Другое наз. Точечно-векторная аксиоматика. Структура евклидовой геометрии в аксиоматике Вейля это <
1. Группа: аксиомы векторного пространства А1: A2: A3: A4: A5: A6: k( A7: (k A8: 2. Группа: dim v=n n=1 - прямая n=2 -плоскость n=3 –трехмерное пространство Размерность равномерно и означает, что в 3. Группы скалярного произведения
A10: A11: A12: A13: 4. Группа
A, B –точки A14: Единственность откладывания вектора
Vгр. L1=(1,0) L2=(0,1) тогдалюбойвектор a =(a1,a2)=a1(1,0)+a2(0,1)= a1L1+ a2L2 k1L1+ k2L2=0 0=k1L1+ k2L2= k1(1,0)+k2(0,1)= (k1,0)+(0, k2)=(k1 k2)=(0,0)=0 ó k1=0 и k2=0 вбаз.(L1 L2) dim U=1 a=(a1,a2) b=(b1b2) a+b=def= a1b1+a2b2 aa=((a1,a2) (a1,a2))=a12+ a22≥0 a12+ a22=0 ó a1=a2=0 a=(0,0) ч.т.д A=(x1y1) B=(x2y2) G(A,B)=AB=(x2-x1,y2-y1) A14: A=(x1y1), a=(a1,a2) Ǝ! B=(x1+ a1, y2+ a2) AB=a C=(x3y3) AB+BC=(x2-x1,y2-y1)+ (x3-x2,y3-y2)= (x2-x1+ x3-x2,y2-y1+ y3-y2)= (x3-x1,y3-y1)=AC Таким образом построена модель Gw Евклидовой плоскости на основе теории IR. Это означает, что аксиомы Gw непротиворечивы, если не противоречива теория IR. III. Аксиомы размерности III1: Существует три линейно независимых вектора, т.е. если. III2: Любые четыре вектора линейно зависимы, т.е. если. Всякая система трех линейно независимых векторов называется базисом данного трехмерного векторного пространства. Теорема: Всякий вектор векторного пространства можно разложить, и притом единственным образом, по векторам базиса. Числа x1,x2,x3 называются координатами вектора в базисе [2]. Аксиоматика Погорелова. I Аксиомы принадлежности: 1) Через 2 точки проходит единственная прямая. 2) Каждая прямая содержит 2 точки и существуют 3 точки не лежащие на одной прямой. II Аксиомы порядка: 1) Из 3-х точек на прямой одна единственная лежит «между» двумя другими. 2) Если прямая l в пл-ти, то прямая разбивает плоскость на 2 полуплоскости, так что если A и B в одной полупл-ти, то l не пересекает отр АВ. Если А и В в разных полупл-тях, то l пересекает АВ. Следствие: Из аксиомы II2 вводится понятие треугольника АВС сост из 3-х отрезков и 3-х точек не лежащих на одной прямой.
3.Аксиомы длины отрезка и меры углов: 3.1 Каждый опред.отрезок имеет опред.длинну(не отрицдействит.число) |АВ|=|АМ|+|МВ|. После этого логично вывести получ.группы на прямой.Выбираем точку О. О разбивает прямую на 2 полупрямые L «разбивает плоскость на 2 части». Одна полупрямая обзн.положительно на пр-р ОА, вторая ОС-отрицательной, тогда х точки, А – длинна отрезка|ОА|,х-точки хС=-|ОС| 3.2 Каждый угол имеет опр. меру 0<Q<180. Каждый угол имеет определенную гр-ную меру. <hl=r=Q, 0<Q<180. Если m между hиl, о <hm+<ml=<hl или α+β=γ Свойство аддитивности: - разверн. угол,<hl=180 A В треуг. АВВ1 m пересекает АВ Геометрия Лобачевского. Сущ 3 класса метрических геометрий 1. Евклидова геометрия 2. Сферическая геометрия(в другом варианте эллиптичгеом Римана)
3. Неевклидова геометрия Лобачевского. Евклидова геом (Начала Евклида 3001 до н.э) Позднее было описание сфер геом. Исследование 5 постулата на основании аксиом Евклида. На ходе эти док-ва содержали ошибки, тем не менее они фактически способствовали открытию некоторых фак-в неевклгеомлобачевского. Практически все крупнейшие мат-ки средних веков и нового времени занимались док-вом 5 постулата, имели след причину:неверноисп утверждения как бы очевидное но эквиволентное постулату Примеры. Утверждэкв 5 постулату. 1) Если 2 прямые на пл-ти не пересек, то расстояние от точки одной прямой до второй(длины периода) постоянна или ограничены в совркупности. Рис 1. l1∩l=пустому мн-ву. А1А перпендикулярно lро(А1А)=|А1А|=ро(А1l) 1.1 p(А1,l)=const; |p(А1l)|<k для любых А1 2) Сумма углов в треугол (любого) равна 180. Док-во. Аксиома паралельности(через В сущl1||l)=> в треугол АВС сумма углов=180 или пи. l1∩l=пустому множеству. Из единственности паралел прямых =>l/=l//, следов α+β+γ=180 как развернутый угол сумма углов в треуг АВС 3)Рис. Сумма углов в треугол постоянная=>сумма углов =180. Система: Ԑ1+Ԑ2=п f1+f2=п по предположению α+β+γ=α+Ԑ1+f1 (**) Сумма EFBC: β+γ+ Ԑ2+ Ԑ1+ f2 (***) И з (*)=> Ԑ1+Ԑ2+f1+f2=2п (**)=>β+γ+ Ԑ2+f2=2п 4) Рис. Сущпрямоугол и квадраты 4-х угольники Ламберта Угол А=углу В=углу С=п/2; δ=углу Д=1 1.δ<=п/2(δ>=п/2 не может быть. 2.δ=п/2 евклидова геометрия 3.δ<п/2 Гипотеза острого угла. Предпологая, что выполняется гипотеза он предпологал найти противоречие. Он заметил, что между фор-ми неевклгеом и фор-ми сферичгеом есть сходство.Онпредпологал, что это геомвыпол на какой-то мнимой сфере. 5) Площади треугольников неограничены в совокупности т.есущ треугольники неограниченно большой площади Рис. δ1<δ2<δ3. Строго возрастаем мб предел ≠0. Рис. Кси-аюсолют. Uvt- предельный треугол. Площадь любого треугол будет < предельного, поэтому ограничены 6) Через любые 3 неколлинеарные точки можно провести окружность(в неевклидгеомлобач кроме прямых и окр есть орициклы и эквидистанты) 7) Сущ подобные, но неравные треугол. В неевклгеом имеет место 4-ый признак равенства: если углы треуголсоотв равны, то треугол равны. На сфере мы выйдем на сферу др радиуса. Замечание. Все евклгеом данной размерностиизоморфны (изометричны) Сферы могут быть произвол радиуса. В неевклгеомсущпл-ти для любого радиуса 8) Через точку вне прямой можно провести не более одной прямой в этой же пло-типаралельноl. 1826 г Лобач сделал доклад о сущнеевклгеом в которой выпол все аксиомы евклгеом за одним источникам:вместо аксиомы паралельности Евклида выполакспаралельностиЛобач:через точку вне прямой в данной пл-ти проходят по крайней мере 2 прямые не пересекающие данную. Рисунок. Из этой акс след, что через точку Апрох бесконечно много прямых пересек данную и сущ 2 положения таких прямых мд которыми все остальные прямые находятся. l1∩l=пустому множеству. L2∩l=пустому множеству. Рис. Отрезок [BD1] разбив на 2 x1ᴗx2=[BD1]. Если E1?x1, то AE1 пересекает l. Если D2?x2, то AD2 не пересекает l. По св-вудейст чисел сущ граничная точка F, кот разделяет х1 и х2т.е если берем точку выше F-не пересекает, если ниже-пересекает cl. Покажем. Что F?x2,,AF пересекает l. Предпол, что AF∩l=F/, x1∩ x2=пустому мн-ву.F?x1, AF∩l=пустому мн-ву. F1(справа от F/), AF1/∩BD1=F1, AF1/∩BD=F1, F1?x2(т.кF граничная точка,AF1пересl => против) Прямая AF-предельное положение среди всех прямых пересl, симметрично относ ABсущ предельно положAC. Эти 2 прямые назпаралельнымиl справа и слева остальные прямые m1m2 не пересек lназыв расходящимися с l. Зависит от x(α=п(х), x=|AB)-|угол паралельности. В Евклгеомгеом α=п/2/ α=П(х)=2arctgl–x/RгеоЛобач где R-радиус кривизны пл-ти лоб; R-большое, то x/Rприбл=0, αприбл=п/2. При больших радиусах кривизны угол паралел-ти не отличен от прямого. Отличие ральнойгеом от Евкл может выразится в сумме углов треугол. Если оно меньше п, то геомнеЕвкл. ЛОбачпредпол изменить углы треугол с вершинами наход в звездах. В конце 20 в было установлено что расшир вселенная в различных постр этого расширения(замедл, пост, ускор) соотв 3 классич геом. Вариант ускорения расширения вселенной соотв гипербол геоЛобач, на небольшом расстоянии различны Евкл.,неевклгеом не могут быть измерены Классические геометрии. Наиб.общими пр-вами явл. топологические и метрические пр-ва. Вводится Риманова метрика 2 2 2 ds =g11 dx +2g12dxdy +g22dy Далее вычисляется кривизна К многообразия л=0-евклидова геометрия к<0- геометрия Лабочевского к>0- сферич или элиптич геометрия Римана Различия: Сферичгеом в любойточке к=1/R>0 Сферич прямые представимы в виде окр Евклидова геом и сферичгеом исследованы Неевклгеом Лобачевского содержит много проблем и она сложнее евклидовой и сферич,но между ними есть зависимость. Пл-стьЛобочевского и евклидова пл_тьгомоморфичны. в трехмерное евклидово пр-во помещена и двумерная сфера, а пл-ть Лобачевского нет. Смысл геом. Лобачевского: 1в трехмерном евклидовом пр-ве сущповерхности,на кот сущсферичечкая геометрия 2Евклидова геометрия орисфере 3 двумерная геом Лобачевского на эквидистанной поверхности Виды классич. геом.: 1евклидова 2 Лобачевского 3 сферич и эллиптич Римана Модель Клейна III2. Данное определение неевклидовой геометрии Л2: Удобно определять неевклид движения через преобразования (проективные, гиперболические, гомологии). F(A|→A) – l-ось гомологии, Р – центр. \ Строим образ. Р?АА|, Р?BB|, ۷A,B Если точка М=АА ∩l, то (РМ,АА´)=1 ↔ f2=id или f=f-1, f – инволюция.
Гиперболические гомологии f2=id получаются, если l и Р – поляра и полюс относительно овала ξ. ABCD – полный 4-хугольник, вписанный в овал.
A,B,C,D - вершины P,Q,R’ – диагональные точки PR=l, (MN,RQ)=-1, (LL’,RQ)=-1 PL=m, PL’=m’ – касательные PQR – автополярный треугольник, каждая сторона которого, явл полярой противоположной вершины. Все неевклид движения 1-го рода явл композицией симметрий. Sl=f Вопросы к экзамену 1. +Множества. Отношения. Примеры. 2. +Математические структуры. Примеры. 3. +Модели. Примеры. 4. +Изоморфизм. 5. +Аксиоматические теории. Непротиворечивость. 6. +-Независимость аксиом. 7. +-Полнота. Роль теории множеств. 8. +Аксиоматика Вейля. 9. +Непротиворечивость аксиоматики Вейля. 10. +Простейшие следствия аксиоматики Вейля. 11. + Аксиоматика Гильберта. I и II группы. 12. + Аксиоматика Гильберта. III, IV, V группы. 13. +Аксиоматика Погорелова. 14. +Непротиворечивости аксиоматики Погорелова. 15. +Геометрия Лобачевского. 16. + Модель Клейна. 17. + Непротиворечивость геометрии Лобачевского. 18. +Модель Пуанкаре. Множества и отношения. Примеры. Если X- мн-ва,то
P(x)-мн-ва всех подмножеств Х. Отношение Примеры 1. n=1 2. n=2 бинарное отношение. 1) E – мн-во точек евклидовой плоскости, L – мн-во всех прямых.
2) S – мн-во всех треугольников на плоскости или прстранстве. Среди бинарных отношений выделяются отношения «эквивалентности» которые удовлетворяют 3 свойствам: рефлексивность, симметричность, транзитивность. 3. n=3 тенарное отношение E -мн-во точек пространства евклида.
4. Отображение (ф-ция) х,у - множества f: х -> у х->f(х)=у
5. Алгебраические операции определяются через отоброжения и поэтому также явл. отношением.
f: 6. Скалярное произведение G: 7. Меорина M – пространство точек
8. Откладывание вектора E - пространство точек
Математические структуры. Примеры Основным методом в современной математике является аксиоматиче- ский метод в теоретико-множественном понимании, тесно связанный с поня- тием математической структуры. Пусть А1,А2,А3,...,Аn - непустые множества. А1 ЧА2 ЧА3 Ч...ЧАn - прямое (декартово) произведение этих множеств, т.е. множество всех упоря- доченных n-местных кортежей (a1;a2;...;an), элемент ai которых, стоящий на i-ом месте, принадлежит множеству Ai,i =1,2,...,n. В теоретико-множественной записи: А1ЧА2 ЧА3 Ч...ЧА ={(a1,a2,...,an)|ai∈Ai}. n Определение 1.1.1. Любое подмножество декартова произведения множеств А1 ЧА2 ЧА3 Ч...ЧА называется n-арным (или n-местным) отношением δ, nопределенным во множествах А1,А2,А3,...,Аn. Замечание. Из определения имеем: 1) δ ⊂А1ЧА2 ЧА3 Ч...ЧАn. 2) Элементы (a1;a2;...;an)(ai∈Ai,i =1,2,...,n) находятся в отношении δ,ес- ли (a1;a2;...;an)∈δ. 3) Если А1 = А2 = А3 =...= Аn = A, то А1 ЧА2 ЧА3 Ч...ЧАn = An - n-аядекар- това степень множества A. 4) Если δ ⊂An, то говорят: на множестве A определено n-арное отношение δ. 5) В случае бинарного отношения δ ⊂A1 ЧA2 вместо (a1;a2)∈δ пишут a1δa2 - «a1 находится в отношении δ с a2». Например, отношение равенства на множестве R всех вещественных чисел – бинарное отношение. 6) Пусть на множестве A определена алгебраическая операция (внутренний закон композиции) ϕ: AЧA→A. Ее можно рассматривать как тернарное отношение δ ⊂AЧAЧA= A3, где δ ={(a,b,c)∈A3 |ϕ(a,b) = c}, a,b,c∈A. 7) Пусть на множестве A определен внешний закон композиции f с множе- ством операторов Λ: f:ΛЧA→A. Его можно рассматривать как тернарное отношение, определенное на множе- ствах Λ,A при помощи подмножества δ ⊂ΛЧAЧA, т.е. δ ={(λ,a,b)∈ΛЧAЧA| f (λ,a)=b}, λ∈Λ, a,b∈A. Рассмотрим конечную систему различных непустых множеств А1,А2,А3,...,Аn. Пусть, например, n= 3. 7 Пусть σ ={δ1,δ2,...,δk} - некоторая система тернарных отношений, оп- ределенных на множествах А1,А2,А3 и обладающих свойствами α1,α2,...,αt. То есть δi - это такое подмножество декартова произведения А1ЧА2ЧА3, которое обладает всеми свойствами α1,α2,...,αt одновременно. Может быть, что существует не одна, а несколько таких систем отно- шений σ ={δ1,δ2,...,δk}. Например, ϕ - алгебраическая операция на множе- стве R действительных чисел: ϕ:RЧR→R (т.е. ϕ можно рассматривать как единственное отношение δ ={(a,b,c)∈R3 |ϕ(a,b)=c}, a,b,c∈R). Пусть отношение δ обладает свойством коммутативности α1:ϕ(a,b)=ϕ(b,a)∀a,b∈R. Можно указать два знчения отношения δ, обладающего свойством α1 (т.е. две коммутативные операции на R): δ′ - сложение, δ′′- умножение, т.е. δ′ ={(a,b,c)∈R3 |a+b=c}, δ′′ ={(a,b,c)∈R3 |a⋅b=c}. Пусть Τ - непустое множество всех систем σ ={δ1,δ2,...,δk} отноше- ний, каждое из которых обладает заданными свойствами α1,α2,...,αt. Определение 1.1.2. Элемент σ∈Τ определяет на множествах А1,А2,А3 математическую структуру рода Τ. Определение 1.1.3. Явно сформулированные свойства α1,α2,...,αt, оп- ределяющие множество Τ, называются аксиомами структуры рода Τ. Определение 1.1.4. Множества А1,А2,А3 называются базой структуры рода Τ. Таким образом, математическая структура рода Т представляет со- бой одно или несколько множеств А1,А2,А3,...,Аn(образующих базу струк- туры), элементы которых произвольной природы (основные, неопределяемые понятия данной теории) и находятся в некоторых отношениях δ1,δ2,...,δ (называемых основными неопределяемыми отношениями), удов- летворяющих аксиомам α1,α2,...,αt. Аксиомы иногда характеризуют не одну с точностью до изоморфизма, а некоторое множество математических структур. Совокупность всех струк- тур, определенных данной системой аксиом Σ ={α1,...,αt}, называется родом Т этих структур. Совокупность предложений, которые можно вывести логическимпу- тем из аксиом структуры, называется теорией структуры рода Т. В 30-х годах ХХ в. Н. Бурбаки определил математику как науку о ма- тематических структурах. Математические структуры подразделены им на три вида: алгебраические, порядковые и топологические. Евклидово, псевдо- евклидово, риманово, псевдориманово пространства, пространственно- временной континуум являются примерами структур топологического типа. 8 Рассмотрим простейшие структуры алгебраического типа. Всем струк- турам одного и того же рода дают специальное название: структура группы, структура n-мерного векторного пространства и др. Пример 1.1.1. (структура группы). Система σ ={δ1,δ2,...,δk} отноше- ний состоит из одного тернарного отношения δ ⊂GЧGЧG=G3, соответст- вующего алгебраической операции: ϕ:GЧG→G (т.е. ϕ можно рассматривать как единственное отношение δ ={(a,b,c)∈G3 |ϕ(a,b)=c}, a,b,c∈G). База состоит из одного множества G. Три аксиомы системы аксиом Σ ={α1,α2,α3} структуры группы: α: ∀a,b,c∈G:ϕ(ϕ(a,b),c)=ϕ(a,ϕ(b,c)) - аксиома ассоциативности; α2:∃e∈G∀a∈Gϕ(a,e)=ϕ(e,a)=a - существование нейтрального элемен- та; α3:∀a∈G∃a′∈G ϕ(a,a′)=ϕ(a′,a)=e - существование симметричного элемента. Пример1.1.2. (структура n-мерного векторного пространства над заданным полем). База состоит из двух множеств – основного множества V (его элементы - векторы – основные неопределяемые понятия); вспомогательного множест- ва K(его элементы условно называются скалярами). Система отношений σ ={δ1,δ2,...,δk} состоит из двух тернарных отношений: δ1 ⊂KЧVЧV, δ1 ={a, xr, yr | f (a, xr)= yr}, a∈K, xr, yr∈V; δ2 ⊂V ЧVЧV =V3, δ2 ={(ar,br,cr)|ϕ(ar,br) = cr}, ar,br,cr∈V. Аксиомы структуры векторного пространства V над полем K: α1:∀λ,μ∈K∀ar∈V f (λ, f (μ,ar)= f (λμ,ar); α2:∀λ,μ∈K∀ar∈V f (λ+μ,ar)=ϕ(f (λ,ar), f (μ,ar)); α3:∀ar∈V f (1,ar)=ar; α ∀r r∈∀λ∈ λ ϕ r r =ϕ λ r λ r; 4:a,b V, K f (, (a,b)) (f (,a), f (,b)) α5:∃0r∈V ∀ar∈Vϕ(0r,ar) =ϕ(ar,0r) = ar; α∀ar∈V∃ −ar∈V ϕar −ar =ϕ −arar = r; 6: () (,()) ((),) 0 α7:ϕ(ar,br)=ϕ(br,ar)∀ar,br∈V; α8:ϕ(ar,ϕ(br,cr))=ϕ(ϕ(ar,br),cr)∀ar,br,cr∈V. Таким образом, теория структур рода Т – это множество предложе- ний (теорем), являющихся логическими следствиями аксиом структуры рода Τ. Предметом математики являются математические структуры. Основ- ной метод математики – дедуктивный аксиоматический (от общих акси- ом к частным следствиям из них): - вводятся неопределяемые, первичные понятия структуры; - вводятся основные отношения; - структуры строятся с помощью аксиом; - затем, используя законы логики, строится теория структур данного рода. Модели. Примеры. Модели(интерпретации)если даны 2 аксиоматические теории S(«старая»), T(«новая»),то построить модели теории T на основе S означает следующее: 1)первоначальное понятие Т определяется на основе S
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.199.188 (0.388 с.) |
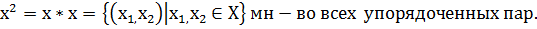
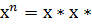 …=
…= 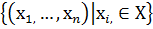 - мн-во всех наборов.
- мн-во всех наборов.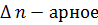 на множестве Х – это
на множестве Х – это 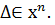 Если
Если 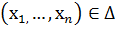 , то говорят
, то говорят 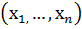 находится в отношении
находится в отношении  .
.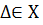 наз. Унарное(одинарное) отношение. Это означает, что каждые элементы мн-ва выделены.
наз. Унарное(одинарное) отношение. Это означает, что каждые элементы мн-ва выделены.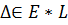 (A,
(A, 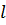 )
) 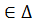 <=> А
<=> А 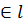 - инциндентность или принадлежность.
- инциндентность или принадлежность.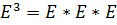
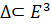 (A,B,M)
(A,B,M) 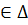 <=>
<=> 
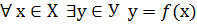
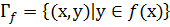 гр. Ф-ции.
гр. Ф-ции.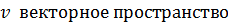
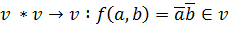
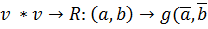 ) =
) = 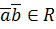
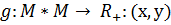 ->
-> 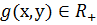 - неотрицательные числа
- неотрицательные числа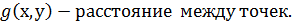
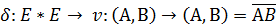
 >
> - пространство точек
- пространство точек - векторное пространство
- векторное пространство сложение векторов
сложение векторов умножение векторов
умножение векторов -скалярное произведение
-скалярное произведение -откладывание векторов
-откладывание векторов
 )+
)+  =
=  +
+ 

 :
: 

 )= (k
)= (k  , k
, k 
 =
= 

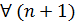 вектор линейно-независимый
вектор линейно-независимый

 =
= 
 +
+ 
 =
= 



 Основное свойство сложения векторов
Основное свойство сложения векторов  +
+  =
= 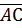
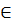 h,B
h,B  m пересечет АВ(m проходит через О и
m пересечет АВ(m проходит через О и  BB1).m и BB1 = М2 в треуг АА1В1 m пересекает BB1 .Независимо от выбора отрезка m пересекает его.
BB1).m и BB1 = М2 в треуг АА1В1 m пересекает BB1 .Независимо от выбора отрезка m пересекает его.




