Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елемент області відбуття може бути поєднаний у кортежах з де-
кількома елементами області прибуття. Підмножина цих елементів у області прибуття є образ елемента з області відбуття.Якщо дляеле-мента області прибуття відповідності виділити підмножину пов’язаних з ним елементів області відбуття, то ця підмножина матиме назву прообраз елемента області прибуття. Якщо множина A має відображен-ня на множину B, а множина B має відображення на множину С, то прообраз елемента з множини B в множині A є множина предків елемента, а образ елемента з множини B у множині С є множина нащадків елемента. Символіка при відображеннях:
j: A®B (це операція відображення, j - ім’я відображення, A – множина відбуття, B – множина прибуття), B = ГА (Г - ім’я відображення, A – множина відбуття, B –множина прибуття).
2.8 Відношення на множинах
2.8.1 Визначення Якщо X – множина, тоді ГÍXn(Xn– n-разовий декартів добуток множини X) і Г звуть n-місним відношенням на множині X. Елементами множини Xnє впорядковані множини (кортежі) довжини n або n-ки (енки). Якщо n = 2 відношення має назву - бінарне, якщо n = 3 - тернарне, взігалі можлива назва n-арне. Приклад використання відношення для часткового подання таблиці множення полягатиме у на- ступному. Бінарна операція множення має два операнди. Разом з резуль- татом операції рядок у таблиці множення матиме три числа, тобто, може бути описаний кортежем довжини 3. Тому таблицю множення чисел, скажімо, від 1 до 4 може бути подано як тернарне відношення на мно- жині X={x| (xÎZ)Ù(x³1)Ù(x£16)}, але замість рядків
1· 1=1 2· 1=2 3· 1=3 4· 1=4 1· 2=2 2· 2=4 3· 2=6 4· 2=8 1· 3=3 2· 3=6 3· 3=9 4· 3=12 1· 4=4 2· 4=8 3· 4=12 4· 4=16
маємо ГÍXn, де Г={(1,1,1),(1,2,2),(1,3,3),(1,4,4),(2,1,2),(2,2,4),(2,3,6), (2,4,8),(3,1,3),(3,2,6),(3,3,9),(3,4,12),(4,1,4).(4,2,8),(4,3,12),(4,4,16)} Властивості відношень та операції над відношеннями вівчає алгебра відношень або реляційна алгебра. Реляційна алгебра послуговує теоретич- ною основою для побудови реляційних баз даних, широковживаних ком- п’ютерних інформаційних технологій. Зберігання табличної інформації у вигляді множин кортежів дає можливість економити пам’ять комп’ютера, а операції пошуку та оновлення інформації часто зведені до теоретико- множинних операцій над множинами кортежів. Бінарні відношення можна разглядати як відповідності, у яких
Множина відбуття та множина прибуття є одна й та ж множина, тобто, R=(A,A,Q) або R=(A,Q), де QÍA´A. Є декілька відомих різновидів бінарних відношень, які можна розрізнити в залежності від того, які вони мають властивості.
2.8.2 Властивості бінарних відношень
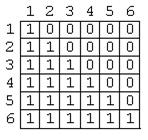
У подальшому вираз xRy означатиме, що елементи x та y перебу- вають у відношенні R, де R=(A,Q), QÍA´A, та що кортеж (x,y) вхо- дить до складу множини Q, а вираз xRy має значення “істинний”. Нижче подано перелік властивостей та умов їх наявності. Рефлексивність,умова наявності: xRx – завжди “істинний”. Антирефлексивність, умова наявності: xRx – завжди “хибний”. Симетричність, умова наявності: xRy®yRx, тобто, при наявності у множині Q кортежа (x,y) у множині Q обов’язково є кортеж (y,x). Несиметричність, умова наявності: хоча б одноразове порушення cиметричності, тобто, при істинному xRy вираз yRx хоча б одноразово хибний. Антисиметричність, умова наявності: завжди при істинному xRy вираз yRx є хибний, а xRx може бути будь-яким. Транзитивність, умова наявності: при істинних xRy та yRz завжди має бути істинним xRz. Хоча б одноразове порушення виключає транзитивність так само, як і відсутність позитивного прикладу. Задання відношеньможе бути виконане будь-яким способом задан- ня множин. Для бінарних відношень на скінченних множинах можливе задання у вигляді матриць. 2.8.3 Матриця бінарного відношення Матриця бінарного відноршення на множині X={x1,x2,…xm} це квадратна матриця з m.m елементтами, у якій елемент сij, що стоїть на перехресті i-го рядка та j-го стовпця має значення: 0 - якщо xiRxj має значення “істинний”, 1 - якщо xiRxj має значення “хибний”. Приклади: 1) Треба побудувати матрицю бінарного відношення “ xi³ xj“ на підмножині цілих чисел X={1,2,3.5.6.4) та визначити властивості відно-шення. Розв’язок у наступному. Маємо відношення R=(X,Q), де Q={(2,1),(3.1),(5,1),(4,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),(6,3),(5,4),(6,4), ,(6,5),(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}. У кожному кортежі множини Q пер- ший елемент більше або дорівнює другому. На матриці (рисунок 2-9) оди-ниці розташовані у клітинах, де перший елемент кортежа взято з елементів
множини X, якими позначені рядки матриці, а другий елемент кортежа
взято з елементів множини X, якими позначені стовпці матриці Рис.2-9 Матриця бінарного відношення xi³xj Відношення має такі властивості: рефлексивність – тому, що у множині Q наявні всі кортежі з X´X, з однаковими першим та другим елементами; на матриці це виглядає як наявність одиниць у всіх клітинах головної діагоналі; несиметричність – тому, що є приклад, коли кортеж (нехай це буде кортеж (4,1)) є у складі множини Q, а симетричний кортеж (це буде кор- теж (1,4) там відсутній (на матриці клітина, симетрична відносно головної дїагоналі міститиме 0); антисиметричність – тому, що немає жодного прикладу симетрич-них відносно головної діагоналі одиниць на матриці та кортежів у множи-ні Q, у яких елементи є переставлені (це підсилена несиметричність, коли вона є, про несиметричність іноді не згадують, бо несиметричність присутня обов’язково); транзитивність - тому, що немає жодного спростовуючего прикла-ду ланцюжка з двох кортежів у множині Q, таких, у яких однакові дру- гий елемент першого та перший елемент другого кортежа, для яких був би видсутній у множині Q кортеж, що складається з першого елемента першого кортежа та другого елемента другого кортежа. Це тому, що, якщо a³b, а b³c, то завжди a³c.
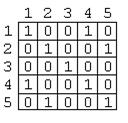
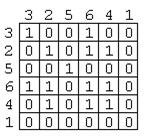
2) Треба побудувати матрицю бінарного відношення “ мати однако-ву остачу від ділення на 3 ” на підмножині цілих чисел X={1,2,3,4,5} та визначити властивості відношення. Розв’язок такий. Матрицю показано на рис.2-10. Рис.2-10 Матриця бінарного відношення “мати однакову остачу від ділення на 3”. Властивості відношення – рефлексивність, симетричність, транзитив-ність. 3) Треба побудувати матрицю бінарного відношення “ мати спільний дільник, відмінний від 1” на підмножині цілих чисел X={1,2,3,4,5,6} та визначити властивості відношення. Розв’язок - матрицю показано на рис.2-11.
Рис.2-11 Матриця бинарного відношення “мати спільний дільник, відмінний від 1”
Властивість відношення – симетричність і тільки. Транзитивність по- рушена наявністю спростовуючого прикладу: кортеж (2,6) присутній у множині кортежів, бо числа 2 та 6 мають спільний дільник 2, кортеж (6,3) створює ланцюжок з кортежем (2.3) і теж присутній у множині корте-жів, бо у чисел є спільний дільник 3. Але кортеж, який будуємо з лан-цюжка (2,3) відсутній у множині кортежів, бо числа 2 та 3 не мають спільного дільника, відмінного від 1.
2.8.4 Операції над відношеннями 2.8.4.1 Композиція відношень. Для відношень R1=(A,Q1) та R2=(A,Q2) може бути побудована композиція R=(A,Q)=R1°R2, множина Q може бути побудована з множин Q1 та Q2 за правилами композиції від- повідностей (див. 2.7.3). 2.8.4.2 Теоретико-множинні операції над відношеннями є операції над множинами кортежів: R1ÈR2 = (A,Q1ÈQ2), R1ÇR2 = (A,Q1ÇQ2), R1\R2 = (A,Q1\Q2), R1ÅR2 = (A,Q1ÅQ2). 2.8.4.3 Обернене відношення R-1=(A,Q-1); xRyÎQ, yRxÎQ-1. 2.8.4.4 Доповнення відношення __ R=(A,(A´A)\Q) (9)
2.8.5 Відношення еквівалентності
Відношення має таку назву, якщо воно рефлексивне, симетричне та транзитивне. Відношення об’єднує елементи у класи еквівалентності за відповідною ознакою. Приклади відношень еквівалентності:
відношення рівності на будь яких множинах,
відношення паралельності на множині прямих ліній на площині, відношення подібності на множині трикутників, відношення “мати однакову остачу при діленні на 3 на множині натуральних чисел” та таке інше. Як побачити, що це відношення екві-валентності? Розглянемо відношення на множині паралельних прямих. Кожна пряма лінія паралельна сама собі - це рефлексивність. Якщо пряма лінія АВ паралельна прямій BC, то пряма BC теж паралельна прямій AB - це симетричність у відношенні. Якщо пряма AB паралельна прямій BC, а пряма BC паралельна прямій DE, то пряма AB паралельна прямій DE - це транзитивність! Вимоги до відношення еквівалентності віконано.
2.8.6 Відношення порядку
Відношення нестрогого порядку має таку назву, якщо воно реф-лекcивне, антисиметричне, транзитивне. Типові позначки такого від-ношення - ”³”, ”£ ”, ”Ê”, ”Í”. Відношення строгого порядку має таку назву, якщо воно антиреф- лексивне, транзитивне. Відповідні позначки “ >”,”<”, “ É”, ”Ì”. Множина є такою, що може бути впорядкованою, якщо будь-які два елементи x та y цієї множини є такі, що можуть бути порівняні, тобто, для них має місце x<y або x=y, або x>y. (існують множини, де цього немає).
2.8.7 Відношення домінування
Властивості відношення: антирефлексивність, несиметричність. Транзитивності немає.
3 Схема зв’язків розділів дискретної математики
Подана нижче схема зв’язків розділів дискретної математики має за мету показати, як на основі теорії множин виростає “споруда” ви- щої алгебри з різноманітними відгалуженнями, що часто стають осно-вою розвитку прикладних теорій. Схема у частині “Моделі” ілюструє точку зору, за якою будь-які теоретико-множинні “споруди” можна розглядати як теоретичні моделі реальних об’єктів у галузі інформатики, обчислювальної техніки та таке інше. Схема у частині “Назви розділів” пояснює, які саме назви розділів підручників можуть висвітлювати відпо- відний матеріал, а у частині “Де застосовуватиметься” містить назви навчальних дисциплін або їх розділів (для студентських груп КІТ-1Х,2Х,3Х), що дістають у дискретній математиці відповідний грунт. (Увага, далі таблиці у файлах dm3-17,dm3-18,dm3-19)
(продовження після таблиць) Зрозуміло, що всі наявні на схемі моделі та розділи не можуть бути об’єктами розгляду в межах цієї навчальної дисципліни як за браком часу, так і з міркувань доцільності. У подальшому увагу зосередимо на розгляді елементів математичної логіки, комбінаторної математики, елементів вищої алгебри та графів.
4 Елементи математичної логіки
Математична логіка - розділ математики, який вивчає математичні доведення. Об’єктами досліджень математичної логіки є висловлювання (судження), які або істинні, або хибні, над якими проводяться логічні операції. Іноді математичну логіку називають метаматематикою.
4.1 Предикати
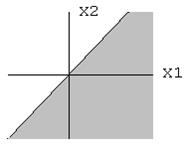
Висловлювання можуть бути аргументами (змінними) у функціях алгебри логіки. Логічні функції є висловлювальні форми, які набувають значення “істинний” або “хибний” в залежності від значень висловлювань - аргументів. Предикати слід розглядати як висловлювальні форми або функції, або функціональні відповідності, що мають більш загальний характер, ніж логічні фенкції, бо аргументи у них можуть бути будь-які, а не тільки логічні значення, але набувають вони тільки значення “істинний” або “хибний”. Формально предикат як відображення може бути визначений так: Р: Мn®B, (10) де В={істиний, хибний}; n- показник степеня (тут декартів добуток). Наприклад, предикат P1(x1,x2)=(x1³x2) має значення “істинний”, якщо x1 не менше ніж x2. Область істиності цього предикату має геометричну інтерпретацію. На рис.4-1 частина площини, що не віще лінії, де x1=x2(затемнена), може бути описана кортежами (x1,x2), у якиx x1³xЗатемнена частина є область істиності предиката P1(x1,x2).
Рис.4-1 Геометрична інтерпретація області істиності предиката P1(x1,x2) Інший приклад. Розглянемо предикат
P(x,y,z,n) = (xn+yn=zn), (11) де x,y,z,n – натуральні числа. Цей предикат при n=2 істинний на всіх єги- петських трикутниках (прямокутних трикутниках з цілочисельними сторо- нами) P(3,4,5,2)= “істинний”, P(5,12,13,2)= “істинний”, P(8,15,17,2)= “істинний”, P(9,12,15,2)= “істинний”. Цей предикат при n>2 є частина формулювання відомої теореми Ферма, відносно якої якої є різні думки (щодо існування хоча б одного прикладу істиності предиката). Ще приклад. Умова закінчення циклічних операцій у програмі може виглядати, як предикат P(x,y,i) = (x=y)Ù(i >100)
4.2 Квантори 4.2.1 Умовні позначки та квантифікація Висловлювання “для всіх x з множини М предикат P(x) є істин- ний” позначають так: "(xÎM)P(x) або "xP(x). Тут позначка " має назву квантор загальності (рос.- квантор общности, англ. – universal generalization) і походить від першої (перевернутої) літе- ри англійського слова All – все, всі. Висловлювання “існує такий x у множині М, для якого предикат P(x) є істинний” позначають так: $(xÎM)P(x) або $xP(x). Тут позначка $ має назву квантор істування (рос.- квантор существования, англ. – existential generalization) і походить від першої (повернутої) літери англійського слова Exist – існувати. З використанням кванторів твердження теореми Ферма виглядає так $(nÎN)$(xÎN)$(yÎN)$(zÎN)((xn+yn+zn)Ù(n>2)) (12) або так $n$x$y$z((xn+yn+zn)Ù(n>2)). (13) У звичайного предиката P(x,y) змінні не є зв’язані умовами, є
вільні. У предиката з квантором "P(x,y) (або $P(x,y)) змінна x є зв’я- зана, а змінна y є вільна. Операція надання кванторів має назву - квантифікація.
4.2.2 Ситуації щодо істинності формул логіки предикатів Формулювання теорем або умов за допомогою предикатів з кван- торами є формули логіки предикатів. Формула логіки предикатів може бути [1]
- виконуваною (рос. выполнимой) у деякій (можливо багатовимірній) області аргументів М, якщо для неї в М існує така підстановка кон-стант замість змінних, що формула набуває значення “істинний”; - тотожно істинною в області М, якщо вона набуває значення “істин-ний” при будь-яких підстановках з М, як, наприклад, формула ___ "x(P(x)ÚP(x)), (14) - тотожно хибною в області М, якщо вона набуває значення “хибний” при будь-яких підстановках з М, як, наприклад, формула ___ $x(P(x)ÙP(x)). (15) 4.2.3 Деякі властивості кванторів Квантор загальності "x має властивість дистрибутивності відносно кон’юнкції, тобто, "x(P1(x)ÙP2(x)) = "xP1(x)Ù"xP2(x), (16)
а квантор існування має властивість дистрибутивності відносно диз’ юнк- ції - $x(P1(x)ÚP2(x)) = $xP1(x)Ú$xP2(x). (17)
Формулу, яка не має зв’язаних змінних, можна виносити за межі дії квантора - "x(P(x)ÚP1(x,z)ÚP(y)) = "x(P(x)Ú P1(x,z))ÚP(y) (18)
Для перетворень кванторних виразів можна скористатись аналогами формул де-Моргана _____ ___ _____ ___ $xP(x) = "xP(x), "xP(x) = $xP(x). (19)
4.2.4 Зв’язок кванторів з функціями алгебри логіки Якщо множина Х є скінченна, а саме, Х={x1,x2,x3,…,xn}, тоді
"xP(x) = P(x1)ÙP(x2)ÙP(x3)Ù…ÙP(xn), (20) $xP(x) = P(x1)ÚP(x2)ÚP(x3)Ú…ÚP(xn). (21)
Ці вирази дають можливість позбутися кванторів у формулах логіки предикатів, після чого доведення, скажімо, тотожної істиності формул полягає в перевірці істиності їх для скінченної кількості підстановок аргументів у предикати. Якщо ж множини не є скінченні, то для дове-дення істиності формул використовують спеціальні правила виводу, які дозволяють здійснити еквівалентні перетворення формул. Результати аналізу істинності формул на скінченних множинах не зав- жди можуть бути поширені на ситуацію з нескінченними множинами, бо
існують формули, здійсненні на нескінченних множинах, але хибні на скінченних множинах. 4.2.5. Про формалізацію доведень та неповноту аксіоматичних си- стем. Німецький філософ Кант стверджував: аксіоми евклідової геометрії апріорно (одвічно, до накопичення досвіду) задані людскій інтуіції. Така позиція похитнулася у XIX сторіччі завдяки математикам Ріману, Больяі, Лобачевському. Вони створили геометричні системи, які не є евклідові, бо замість аксіоми Евкліда про паралельні прямі використали свої варіанти цієї аксіоми. Ріман показав, якщо евклідова геометрія несуперечлива, то і його ріманова геометрія теж несупереч-лива, бо теж послідовно побудована на аксіомах [7]. Якщо взя- ти до уваги те, що повсюдно визнана теорія відносності Ейнштейна ба- зується на рімановій геометрії, то можна погодитись з думкою, що й іншим геометричним системам не уникнути застосування. Але важливо було і те, що не тільки несуперечливість евклідової геометрії перестає бути апріорно очевидною, а ще й тягне за собою несуперечливість конкуруючої системи. Виходить, що питання про несуперечливість систем слід вивчати незалежно від того, як “істинно” системи описують “реальний світ”. На початку ХХ сторіччя німецьким математиком Гільбертом була створена група математиків-формалістів, які створили математичну ло- гіку. Формалізація доведення теореми у ній полягає у тому, що форму-лювання теореми перетворено у рядки символів (квантори, предикати), з котрих застосуванням добре перевірених правил виводу можна одер- жувати нові рядки, і через скінченний ланцюг перетворень дійти (або не дійти) до тотожно істинних формул, що й має означати успішне доведення теореми. Випробувати такий метод доведення теорем форма- лісти спробували на створенні арифметичної логіки, яка була б повною. Тобто такою, в якій можливо було б вивести (як теореми) всі істинні твердження про цілі числа. Задум ніяк не вдавалось завершити. Намагання формалістів припинились, а програма була зруйнована тео- ремою німецького математика Гьоделя про неповноту. Теорема стверд- жує, що будь-яка несуперечлива арифметична логіка є неповною, що існує істинне твердження про цілі числа, які не можна довести засобами цієї логіки. Але можна довести засобами іншої логіки, яка більш загаль- на і обіймає цю. Філософи вбачають у цьому нескінченність пізнання, бо система, що обіймає, теж неповна. Так розроблений математиками- формалістами математичний апарат для формалізації доведень допоміг виявити важливу властивість у відносинах людини і реального світу. 4.2.6 Про теорії алгоритмів та цифрових автоматів Теорія алгоритмів (алгорифмів) з’явилась за 30 років до появи ЕОМ і ставила за мету визначення можливості ефективно обчислити задачу (тобто за скінченну кількість елементарних кроків дійти результату). Ця теорія також має назву - теорія обчислюваності. Щоб теорія мала ознаку строгої математичної теорії, потрібно було визначити поняття машина (абстрактна), алгоритм. Така абстрактна машина (машина Поста[8], машина Т’юрінга) має мінімальну кількість команд (Аж 6 команд у Поста! Це вкрай мало на- віть у порівняння з сучасними RISC-мікроконтролерами, де 30 – 36 команд) та найпростішу пам’ять - нумеровані комірки для зберігання 1 биту інформації в кожній. Така мінімізація спрощувала доведення теорем. Ця глибока та послідовна теорія з специфічними термінами (загальнорекурсивні функції, частково рекурсивні функції та т. ін.) дозволяє чипати такі питання, як, скажімо, “Чи може машина бути розумніше її творця?” або “Чи може машина самовідтворюватись?”[7]. Якщо стан запам’ятовуючого пристрою та стан інших елементів машини представити кортежем, то будь-який алгоритм можна предста- вити послідовністю переходів від одного кортежа до іншого, що є об’єк- том вивчення у “Теорії цифрових автоматів”. Щодо алгоритмізації конкретних задач теорія алгоритмів зараз мало що може додати.
5 Комбінаторна математика
Комбінаторна математика або комбінаторика чипає області бага- тьох розділів математики і ця обставина утруднює її формальне визна- чення. В основному вона має справу з розташуванням елементів у мно- жинах. У типових випадках кількість елементів скінченна, а їх розта- шування зумовлене певними обмежувальними умовами, що витікають з умов конкретної задачи. Розглядаються 2 типи проблем: - проблема існування певних конфігурацій на множинах та - проблема визначення кількості конфігурацій, їх класифікація (перелічувальна задача). Приклад проблеми (задачи) першого типу. Є множина підмножи-на цілих додатних чисел від 1 до 16. Чи можливо розташувати ці чис- ла у квадратній матриці 4´4 елементи так, щоб сума чисел у кожному рядку та у кожному стовпцю була та ж сама. Така конфігуруція (розташування елементів) має назву - латинський квадрат. Колись слу- гувала головоломкою для розваг, тепер має відношення до теорії оп-тимального планування. В задачах другого типу комбінаторній ситуації або комбінаторній моделі треба поставити у відповідність формулу для обчислення кіль- кості конфігурацій (потужності множини конфігурацій). Далі розгляда- тимемо відомі конфігурації, деякі правила та виведемо формули для обчислення їх кількості [5].
5.1 Правило суми Якщо потужність множини S |S|=m, а потужність множини T |T|=n, то потужність множини SÈT за умови SÇT=Æ можна обчислити як |SÈT|=|S|+|T|=m+n (22)
5.2 Узагальнене правило суми Якщо |Ti|=ni, то за умови TiÇTj=Æ, i¹j |T1ÈT2ÈT3È…ÈTk|=n1+n2+n3+…+nk(23)
5.3 Правило добутку Якщо потужність множини S |S|=m, а потужність множини T |T|=n, то потужність множини |S´T|=m×n (24)
5.4 Узагальнене правило добутку Якщо |Ti|=ni, то |T1´T2´T3´…´Tk|=n1×n2×n3×…×nk(25) Потужність декартового добутку дорівнює добутку потужностей множин -співмножників.
5.5 Розміщення с повтореннями або вибірки Конфігурації можна побудувати наступним чином. Задано множину S потужності ½S½=m. З елементів множини S, розмножуючи їх при потребі, формуємо кортежі довжини n
(s4,s1,s2,sm,s1,…,s4,s3,s5) це варіант конфігурації n елементів Кожен такий кортеж може мати деякі елементи множини S, при- пустимі повторення елементів у кортежі. Такі конфігурації (у цьому випадку – кортежі) мають назву “розміщення з повтореннями” (деякі елементи розмістили у кортежі, можливо повторюючи їх) або “вибірки”. Формулу для визначення кількості можливих (різних) кортежів за таких умов формування виведемо, враховуючи наступне. Кортежі довжини n, побудовані з елементів множини S, належать декартовому добутку
S´S´…´S,
n разів
а їх кількість згідно з узагальненим правилом добутку дорівнює
m×m×…×m=mn n разів Тобто, кількість розміщень з повтореннями N=mn, (26)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.70.60 (0.18 с.) |