Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логика как наука и ее значение в познанииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Байгильдин Риза Мирзаевич Кандидат философских наук, зав.кафедрой общеобразовательных дисциплин ГГХПИ. Окончил философский факультет Уральского государственного университета, затем аспирантуру Башгосуниверситета. Научно-педагогический стаж – 26 лет. Стаж работы в органах государственной власти и управления - 9 лет. Сфера научных интересов лежит в области социальной философии - теория деятельности, ее мотивы и основания, проблема потребностей. По результатам исследований опубликовано более 50 научных трудов. Работает над докторской диссертацией. Читает лекции и проводит практические занятия по следующим дисциплинам: философия, логика, социология, политология, демография и др. ЛОГИКА Оглавление Лекция 1. Логика как наука........................... …… 2ч Вопросы для самоконтроля Контрольный тест к теме 1 Лекция 2. История логики............................ …… 2ч Вопросы для самоконтроля Контрольный тест к теме 2 Лекция 3. Основные понятия логики …………..….. 2ч Вопросы для самоконтроля Контрольный тест к теме 3 Лекция 4. Суждение ………….. 2ч Вопросы для самоконтроля Контрольный тест к теме 4 Лекция 5. Умозаключение ………….. 2ч Вопросы для самоконтроля Контрольный тест к теме 5 Лекция 6. Законы классической логики …… ……. 2ч Вопросы для самоконтроля Контрольный тест к теме 6 Лекция 7. Гипотеза............................... …… 2ч Вопросы для самоконтроля. Контрольный тест к теме 7 Лекция 8. Логические основы теории аргументации ……2ч Вопросы для самоконтроля Контрольный тест к теме 8 Глоссарий ………………………………………………… Список основной литературы …………………………… Список дополнительной литературы …………………. Лекция 1. ЛОГИКА КАК НАУКА
Контрольный тест 1. Логика – это: 1. наука об умозаключениях и доказательствах; 2. наука о правилах мышления; 3. наука о формах и законах мышления; 4. наука о формах и законах познания.
2. Формальная логика появилась: 1. в Средние века; 2. в Античности; 3. в Новое время; 4. в эпоху Возрождения.
3. Формальная логика является: 1. символической; 2. аристотелевской; 3. математической; 4. современной.
4. Создателем логики считается древнегреческий философ: 1. Анаксимен; 2. Анаксагор; 3. Пифагор; 4. Аристотель; 5. Математическая или символическая логика появилась: 1. тогда же, когда и традиционная логика; 2. в XVII в.; 3. в XIX в.; 4. в середине XX. 6. Интуитивная логика – это: 1. совершенное незнание законов правильного мышления, приводящее любое рассуждение к многочисленным ошибкам и ложным выводам; 2. стихийно сформированное в процессе жизненного опыта знание форм и принципов правильного мышления; 3. теоретические знания, оставшиеся у человека после изучения курса логики в школе или вузе; 4. полное искажение теоретической логики. 7. Древнегреческие философы, которые изобретали разнообразные приёмы нарушения логических законов с целью доказать всё, что угодно, – это: 1. милетцы; 2. пифагорейцы; 3. софисты; 4. стоики.
8. Истинность мысли по содержанию:
9. Основные формы мышления: 4. представление
10. Целостный образ предмета, возникающий при непосредственном воздействии его на органы чувств: 4. ощущение. Лекция 2. ИСТОРИЯ ЛОГИКИ
История логики продолжительна по времени. Человек во все времена стремился к постижению истины, однако для возникновения учения о правильном мышлении были необходимы определенные условия. Все необходимые для этого факторы появились более двух тысяч лет назад в Индии, Китае, Греции. Логика зародилась и получила дальнейшее развитие как часть философского знания. Процесс развития логики можно разделить на несколько этапов: логика Древнего мира, античная логика, логика Средневековья, логика эпохи Возрождения, Нового времени и, наконец, современная логика. Логика Древнего мира Логика Древнего мира обязана своим появлением философам Китая, Индии и Греции. Известно, что на ранних этапах развития логические знания носили онтологический характер, т. е. законы мышления приравнивались к законам бытия. Большое внимание в этот период уделялось умозаключению, а последнее практически отождествлялось с доказательством. Толчок к развитию логики дала риторика. Ораторское искусство использовало зачатки логических знаний для достижения основной цели говорящего - убеждения слушающих, а не для установления истины, как это имеет место в более поздние периоды. Логический элемент здесь носит характер подчиненный, является как бы составной частью ораторского искусства. Философия как совокупность научных знаний зародилась и развивалась одновременно в государствах древности, имеющих разные взгляды на окружающий мир, подходы к его изучению и соответственно отличающиеся друг от друга философские системы. Древняя Греция Именно здесь проблемы логики были рассмотрены и разработаны наиболее обстоятельно. Логические вопросы здесь рассматривают такие философы, как Парменид и Зенон (представители элейской философской школы), Гераклид, софисты Протагор, Горгий и другие, Демокрит и Аристотель. Деятельность этих философов прямо или косвенно затрагивала вопросы логики. Идеи представителей элейского направления и приверженцев логики Гераклида вступали в конфликт в силу их противоположности. Элейская школа проповедовала метафизические теории, т. е. способ изучения явлений, при котором они рассматриваются отдельно друг от друга и в неизменном состоянии. Гераклитовская философия придерживалась идей диалектики (явления изучаются в развитии и взаимодействии). Главной особенностью, характеризующей философский подход софистов, является то, что они в качестве объекта исследования предлагали человека, а не окружающий мир, как это было раньше. Софисты рассматривали логику не как науку, позволяющую установить истину, а как средство достижения победы в споре. Для этого они сознательно нарушали законы логики. Первым против софистов выступил Демокрит (460-370 гг. до н. э.), принадлежавший к материалистической философской школе. Философская система, созданная Демокритом, содержит учение о бытии, теорию познания, этику и эстетику, космологию, физику, биологию, политику и логику. Он разработал и закрепил в своем трактате "О логике" ("Каноны") первую систему логики. Демокрит считается одним из основателей индуктивной логики, поскольку его трактат основывается на эмпирических началах. Рассматривая суждения, Демокрит выделяет в них субъект и предикат. Проблемами логики занимались также Сократ (469-399 гг. до н. э.) и Платон (428-347 гг. до н. э.). В учении Сократа главным считался метод, который позволял получить истину, а также содержалась идея, что познание любого предмета становится возможным, лишь если свести его к общему понятию и на этой основе судить об этом понятии. Для достижения истины Сократ предлагал ученикам дать определение какому-либо явлению, особенности или характерной черте, присущей окружающему миру или человеку. Затем, если такое определение оказывалось, по его мнению, недостаточно полным или правильным, он, применяя примеры из жизни, указывал на ошибки, допущенные собеседником, а затем изменял и дополнял его. Достижением знания Сократ считал нахождение закономерностей и определение понятия для ряда вещей. В процессе достижения знания учитывались общие черты предметов и различия между ними. Древнегреческий философ Платон был учеником Сократа и разрабатывал теории познания и логики, опираясь на идеи учителя. Используя свои теории, Платон сначала получал новые понятия, а затем старался разбить их на виды и систематизировать. Для этого он использовал свой излюбленный прием под названием "дихотомия", т. е. деление понятия А на В и не В (например, преступления могут быть умышленными и неумышленными, а животные позвоночными или беспозвоночными). Как и в школе Сократа, ученики Академии Платона много занимались получением новых определений. В современной философской науке есть упоминание о курьезном случае, связанном именно с определениями. Платон, описывая человека, сказал, что человек "есть двуногое животное без перьев". Узнав о таком определении, известный философ Диоген ощипал курицу и принес в Академию Платона во время лекции со словами: "Вот человек Платона". Платон был вынужден признать недостаточность своего определения и внес изменения, согласно которым "человек есть двуногое животное без перьев и с плоскими ногтями". Платон создал систему объективного идеализма, согласно которой духовное начало (в отличие от субъективного идеализма) существует независимо от сознания человека. В этой теории Платон использовал деление мира на материальный и идеальный (духовный) и поставил первый в зависимость от второго. Иными словами, материальный мир, по Платону, непостоянен и изменчив, в отличие от идеального, который существует независимо от материи и сознания человека. Идеи он считал вечными и неизменными, а материальный мир как бы проекцией идеального. Иными словами, вещь - лишь отражение идеи. Платон развивал теорию суждения, создал два правила деления понятий, а также отличал отношение различия от отношения противоположности. Таким образом, многие философы Древней Греции работали над вопросами логики, однако ее основателем по праву считается Аристотель Стагирский (Аристотель родился в городе Стагир - именно отсюда пошло его прозвище). Он посвятил себя изучению многих наук, таких как философия, логика, физика, астрономия, психология, риторика и др. Этим предметам посвящены многие его сочинения. Именно Аристотель оформил знания о логике в четкую систему и обнаружил, что знания, откуда бы они ни были получены, всегда имеют языковое выражение. Отсюда он делал вывод, что научные знания есть последовательность высказываний, объединенных логическими связями и выводимых одно из другого. Логику Аристотеля называют формальной или традиционной. Она включает такие разделы, как понятие, суждение, законы правильного мышления, умозаключения, аргументация и гипотеза. Важным достижением Аристотеля является то, что он впервые сформулировал законы правильного мышления: закон тождества, закон непротиворечия и закон исключенного третьего, а также стал изучать человеческое мышление с целью вывести его логические формы. Эти законы были сформулированы в важнейшем сочинении Аристотеля "Метафизика". Аристотель создал теорию силлогизма, рассмотрел теорию определения и деления понятий и теорию доказательства. Главными трудами в этой области являются трактаты "Первая аналитика" и "Вторая аналитика", которые впоследствии наряду с другими работами были объединены в "Органон" - метод, средство или орудие познания действительности. В этом труде содержится мнение о том, что законы логики неразрывно связаны с окружающим миром и с человеком и не могут существовать в отрыве от них. Эт от вывод подтверждает и то, что логика соответствует культуре конкретного общества и отражает характеризующие эту культуру признаки. Например, в индийской логике отсутствует закон исключенного третьего, характерный для логики Аристотеля. По мнению ученых, эта тенденция прослеживается в культурах данных стран в целом. Так, население стран, в которых распространение получила логика Аристотеля, более тяготеет к прямым линиям, что хорошо просматривается на примере суждений о добре и зле, которым характерна бескомпромиссность, а также в архитектуре (античные колонны) и оружии (прямой меч). Восточным же странам ближе линия кривая (мусульманский полумесяц, кривые мечи, большая свобода суждений). Истинным Аристотель считает утверждение, если оно соответствует положению окружающего мира, т. е. отображает реальное состояние вещей. Ложными, таким образом, считались суждения, которые используются не для отображения объективной реальности, а для сознательного или случайного изменения этой реальности, т. е. "подгонки" явлений окружающего мира под необходимый ответ. Иными словами, ложно то, что нарушает существующие связи между вещами или создает новые, существующие только на словах. Отталкиваясь от этой концепции истинности, Аристотель создает свою логику. В заключение необходимо упомянуть о логике стоиков - системе знаний, разработанных приверженцами мегаро-стоической школы, стоиками Зеноном и Хризиппом и мегариками Диодором, Стилпоном, Филоном и Евбулидом. В результате деятельности этой школы современная логика получила анализ логических понятий отрицания, конъюнкции, дизъюнкции и импликации. Задачей логики они видели избавление от заблуждений и создание возможности правильно судить о вещах. Логика должна изучать не только словесные знаки, но и мысли, выражающиеся в них. Выходя за рамки формальной логики, представители мегаро-стоической школы делили логику на диалектику и риторику. К сожалению, представления данной философской школы в области логики лишь частью дошли до нашего времени. Средневековая логика Средневековая логика в основном изучала вопросы модальной логики, теория логического следования, теория семантических парадоксов, а также проводился анализ выделяющих и исключающих суждений. Основными направлениями, рассматривающими вопросы логики, были учения реалистов и номиналистов. Первые считали, что общие понятия существуют независимо от единичных вещей. Номиналисты стояли на противоположных позициях и считали, что общие понятия лишь именуют единичные вещи, которые являются реальными. Следует отметить, что оба эти подхода неверны. Наиболее известными учеными, работавшими над вопросами логики в Средиземноморье, являются Вильям Оккам, Дунс Скотт, Раймунд Луллий, Жан Буридан, Альберт Саксонский. Следует особо выделить Вильяма Оккама, который известен благодаря тому, что создал логическое орудие под названием "лезвие Оккама". Проводником между античной и арабоязычной логикой послужила наука, разрабатываемая в Сирии. Вопросами логики в арабском мире занимались такие ученые, как аль-Фараби, которого считают основателем сирийской логики, Ибн-Сина (Авиценна), Ибн-Рушд (Аверроес). Аль-Фараби являлся идейным последователем Аристотеля. Он комментировал главный труд Аристотеля "Органон". Логика аль-Фараби направлена на изучение научного мышления и рассматривает вопросы истинности, опираясь на концепцию истинности, разработанную Аристотелем. Структура его логики состоит из двух частей, одна рассматривает представления и понятия, а другая изучает теорию суждений, выводов и доказательств. Особое внимание аль-Фараби уделял вопросам теории познания и грамматики. Трактовку работ Аристотеля продолжил Ибн-Сина. Он пользовался переводами и комментариями античных работ, созданных аль-Фараби. Авиценна изучал аристотелевскую силлогистику, прослеживал зависимости и связи между категорическими и условными суждениями, а также выражение импликации через дизъюнкцию и отрицание. Свои идеи ученый закрепил в учебнике "Логика". Самой известной и используемой работой по логике является трактат "Summulae logicales", содержащий ряд новых идей в области логики высказываний. Эта работа принадлежит перу Петра Испанского. Логика Нового времени Иммануил Кант (1724-1804), известный ученый периода Нового времени, предлагал деление логики на два типа - формальную и трансцендентальную. Обычная логика занимается изучением понятий, суждений и умозаключений. Трансцендентальная логика исследует формы мышления, а знание рассматривает как предшествующее опыту и независимое от него. Априорное (a priori - "из предшествующего") знание, таким образом, - это условие опытного знания, которое придает ему оформленный, всеобщий и необходимый характер. Априорные формы логических знаний, по мнению И. Канта, призваны упорядочивать хаос ощущений и предоставлять полную и достоверную информацию. И. Кант отличал логические причины и следствия от реальных причин и следствий, что является важным вкладом в теорию науки. Выражением знания И. Кант считал суждение и делил последнее на два вида: аналитическое и синтетическое. Аналитические суждения не создают нового знания, а лишь дают определение уже существующему. Синтетические суждения могут быть апостериорные (a posteriori - "из последующего"), которые ставятся в прямую зависимость от опыта, происходящие из него, и априорные, от опыта независимые и, более того, даже предшествующие ему. Отсюда видно, что данные два вида противоположны один другому. Необходимо отметить, что и на сегодняшний день в среде логиков и философов нет единства мнения относительно априорных суждений И. Канта. Георг Вильгельм Фридрих Гегель (1770-1831) считается самым известным немецким философом классической школы. Он, опираясь на объективно-идеалистическую основу, разработал систематическую теорию диалектики. Основным понятием этой теории является развитие, под которым понимается характеристика деятельности мирового духа (абсолюта). Абсолют характеризуется сверхвременным движением в области чистой мысли в восходящем ряду все более конкретных категорий (бытие, ничто, качество, количество, мера и т. д.). "Наука логики" начинается с учения о бытии. Категорию "бытие" Гегель трактует как существование вообще вечной идеи в непосредственной элементарной форме. Философская система Гегеля имеет три составляющих ее части: первая - "Логика", которая выступает как тезис, вторая - "Философия природы" - как антитезис, третья - "Философия духа" - как синтез. В свою очередь каждая из трех составных частей имеет три раздела. " Логика" состоит из учения (1) о бытии, (2) о сущности, (3) о понятии. "Философия природы" имеет три раздела: (1) механизм, (2) химизм, (3) организм. Аналогично "Философия духа" подразделяется на субъективный дух, объективный дух, абсолютный дух. Содержание первых разделов каждой из частей системы имеет в ней значение тезиса, вторых разделов - антитезиса, третьих - синтеза. Следует особо отметить, что третий раздел третьей части системы - учение об абсолютном духе - есть не просто один из многих синтезов триадичных категорий, а высший синтез субъективного и объективного духа, в результате которого обретена "абсолютная и полная истина, мыслящая самое себя идея". Таким высшим синтезом, в котором абсолютная идея постигла сама себя, Гегель считал свою философию. Вторая триада системных категорий первой части "Науки логики" выведена Гегелем из категории "наличного бытия", которое обладает внутренней определенностью, т.е. качеством. Качество у Гегеля тождественно с бытием, ибо нечто перестает быть тем, что оно есть, как только утрачивает качество. В единстве с качеством выявляется и внешняя определенность наличного, бытия - количество. Сформулировав в общезначимой форме закон взаимного превращения количества в качество, Гегель тем самым глубоко раскрыл одну из существенных сторон процесса развития - его механизм, как совершается возникновение нового качества.
Вопросы для самоконтроля 1. Логика Аристотеля. 2. Лейбниц Г.В. и математическая (символическая) логика. 3. Диалектическая логика. 4. Развитие символической логики в середине XIX – начале XX веков. 5. Результаты современных логических исследований Контрольный тест 1. Кто из мыслителей открыл закон противоречия и сформулировал его сущность? 2. Какое первоначальное название имела логика – наука, специально изучающая внутреннюю структуру человеческого мышления?
3. Обоснованность мышления – это свойство правильного мышления: 4. Основателем логики следует считать: 5. В каком веке сформировалась логика в качестве самостоятельной науки? 6. Явление, вызывающее к жизни другое явление, – это: 7. Кто из мыслителей открыл закон достаточного основания и сформулировал его сущность? 8. Научный метод, разработанный английским мыслителем XVII в. Ф. Бэконом, называется эмпиризм. Какая логическая форма умозаключения лежит в его основе? 4. анализ 9. Формальная логика появилась: 1. в Средние века; 2. в Античности; 3. в Новое время; 4. в эпоху Возрождения. 10. Математическая или символическая логика появилась: 1. тогда же, когда и традиционная логика; 2. в XVII в.; 3. в XIX в.; 4. в середине XX. Лекция 3. ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ Определение понятий Определение (или дефиниция) понятия есть логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина. С помощью определения понятий мы в явной форме указываем на сущность отражаемых в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов. Так, например, давая определение понятия «трапеция», мы отличаем его от других четырехугольников, например от прямоугольника или ромба. «Трапеция — четырехугольник, у которого две стороны параллельны, а две другие — не параллельны» (1). Приведем еще несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений. «Вещества, растворы которых проводят электрический ток, называются электролитами» (2). «Флорой называют видовой состав растений, произрастающих на той или иной территории» (3). «Естественный отбор — процесс выживания наиболее приспособленных особей, который ведет к преимущественному повышению или понижению численности одних особей в популяции по сравнению с другими» (4). В явном определении понятие, содержание которого надо раскрыть, называется определяемым понятием [ definiendum (дефиниендум), сокращенно Dfd ], а то понятие, посредством которого оно определяется, называется определяющим понятием [ definience (дефиниенс), сокращенно — Dfn ].
Реальные и номинальные определения Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определение будет номинальным. Из вышеприведенных определений (1) и (4)—это реальные определения, а (2) и (3) — номинальные определения. С помощью номинальных определений вводятся также новые термины, краткие имена взамен более сложных описаний предметов. Например, «навыком называют такое действие, в составе которого отдельные операции стали автоматизированными в результате упражнений». Путем номинальных определений вводятся и знаки, заменяющие термины. Например, «Конъюнкция обозначается знаками ^ или &», «С — скорость света», «Тангенс угла α обозначается как tg α» и т. д. В номинальном определении часто раскрывается и этимология того или иного термина. Например, «Термин «философия» происходит от греческих слов «филео» — люблю и «софия» — мудрость, что означает любовь к мудрости (или, как говорили раньше на Руси, любомудрие)». Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Номинальные определения часто встречаются в учебниках по математике для средней школы. Так, в курсе геометрии встречаются следующие номинальные определения: «Конус называется круговым, если основание его — круг» или «Круглый конус называют конусом вращения». Определения делятся на явные и неявные. Явные определения — это такие, в которых даны Dfd и Dfn и между ними устанавливается некоторое отношение равенства, эквивалентности. Самое распространенное явное определение — определение через ближайший род и видовое отличие. В нем устанавливаются существенные признаки определяемого понятия. Примеры. 1. «Правильный многоугольник — многоугольник, у которого все стороны конгруэнтны и все углы равны». 2. «Барометр — прибор для измерения атмосферного давления». 3. «Гротеск — один из способов сатирического изображения жизни, отличающийся резким преувеличением, сочетанием реального и фантастического». Признак, указывающий на тот круг предметов, из числа которых нужно выделить определяемое множество предметов, называется родовым признаком, или родом. В приведенных примерах родовыми являются понятия «многоугольник», «прибор», «способ сатирического изображения жизни». Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих родовому понятию, называются видовым отличием. При определении понятия видовых признаков (отличий) может быть один или несколько. К явным определениям понятий относятся и генетические определения. Они часто встречаются в школьных учебниках. Генетическим называется определение предмета путем указания на способ, которым образуется только данный предмет и никакой другой (это его видовое отличие). Генетическое определение является разновидностью определения через род и видовое отличие. Приведем примеры генетических определений из области химии. 1. Кислотами называются сложные вещества, образующиеся из кислотных остатков и атомов водорода, способных замещаться атомами металлов или обмениваться на них. 2. Коррозия металлов — это окислительно-восстановительный процесс, образующийся в результате окисления атомов металла и перехода их в ионы.
Правила явного определения. Ошибки, возможные в определении 1. Определение должно быть соразмерным, т. е. объем определяющего понятия должен быть равен объему определяемого понятия. чего возникают логические ошибки в определении. Типы этих логических ошибок: а) широкое определение, когда Dfd<Dfn. Такая ошибка содержится в следующих определениях: «Гравитация — это взаимодействие двух материальных тел». «Лошадь — млекопитающее и позвоночное животное». (Здесь понятие «лошадь» нельзя отличить от понятий «корова» или «коза».) Понятие «окружность» неправильно определяется так: «Это фигура, которая описывается движущимся концом отрезка, когда другой его конец закреплен, или фигура, которая образована движущимся концом циркуля». С помощью этого определения нельзя отличить понятие «окружность» от понятия «дуга», так как не указано, что окружность — это кривая замкнутая линия; б) узкое определение, когда Dfd>Dfh. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?). «Производительными силами называются орудия труда, а также и сами люди с их умениями и приемами труда». (В производительные силы входят все средства производства, а не только орудия труда.); в) определение в одном отношениии широкое, в другом — узкое. В этих неправильных определениях Dfd>Dfn и Dfd<Dfn (в разных отношениях). Например, «Бочка — сосуд для хранения жидкостей». С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайник, и ведро, и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей. Аналогичная ошибка содержится в определении понятия «учитель»: «Учитель — человек, обучающий детей». 2. Определение не должно содержать круга. Круг возникает тогда, когда Dfd определяется через Dfn, a Dfn был определен через Dfd. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («ось — это прямая, вокруг которой происходит вращение»). Круг возникает и тогда, когда определяемое понятие характеризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее понятие в качестве его части. Такие определения носят название тавтологий. Тавтологичны такие определения: «Халатность заключается в том, что человек халатно относится к своим обязанностям»; «Количество — это характеристика предмета с его количественной стороны». Логически некорректным является употребление в мышлении (и в речи) тавтологий, таких, например, как масляное масло, трудоемкий труд, порученное поручение, прогрессирующий прогресс, ладанная задача, изобрету изобретение, поиграем в игру, памятный сувенир, подытожим итоги и др. Иногда можно встретить выражения вида: «Закон есть закон», «Жизнь есть жизнь» и т. д., которые представляют собой прием усиления, а не сообщения в предикате какой-то информации о субъекте, так как субъект и предикат тождественны. Такие выражения не претендуют на определение соответствующего понятия: «закон», «жизнь» или др. 3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их - метафорами, сравнениями и т. д. Не будут определениями следующие суждения: «Архитектура — застывшая музыка», «Лев — царь зверей», «Верблюд — корабль пустыни», «Такт — это разум сердца» (К. Гуцков), «Неблагодарность — род слабости» (И. В. Гёте).
Неявные определения Вотличие от явных определений, имеющих структуру Контекстуальное определение позволяет выяснить содержание незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода, если текст дан на иностранном языке, или к толковому словарю, если текст дан на родном языке. Значения неизвестных в уравнениях даны в неявном виде. Если дано уравнение, первой степени, например 10— y =3, или дано квадратное уравнение, например х 2 — 7 x +12=0, то, решая их и находя значение корней этих уравнений, мы даем явное определение для у (у =7) и для х (x1 = 4 и х2 = 3). Индуктивные определения характеризуются тем, что определяемый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивного определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»: 1. 1 — натуральное число. 2. Если n — натуральное число, то n + 1 — натуральное число. 3. Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет. С помощью этого индуктивного определения получается натуральный ряд чисел: 1, 2, 3, 4.....Таков алгоритм построения натуральных чисел.
Правила деления понятий Чтобы деление было правильным, необходимо соблюдать следующие правила. 1. Соразмерность деления: объем делимого понятия должен быть равен сумме объемов членов деления. Например, высшие растения делятся на травы, кустарники и деревья. Электрический ток делится на постоянный и переменный. Нарушение этого правила ведет к ошибкам двух видов: а) неполное деление, когда перечисляются не все виды данного родового понятия. Ошибочными будут такие деления: «Энергия делится на механическую и химическую» (здесь нет, например, указания на электрическую энергию, атомную энергию). «Арифметические действия делятся на сложенне, вычитание, умножение, деление, возведение в степень» (не указано «извлечение корня»); б) деление с лишними членами. Пример этого ошибочного деления: «Химические элементы делятся на металлы, неметаллы и сплавы». Здесь.лишний член («сплавы»), а сумма объемов понятий «металл» и «неметалл» исчерпывает объем понятия «химический элемент». 2. Деление должно проводиться только по одному основанию. Это означает, что нельзя брать два или большее число признаков, по которым бы производилось деление. Если будет нарушено это правило, то произойдет перекрещивание объемов понятий, которые появились в результате деления. Правильные «деления: «Волны делятся на продольные и поперечные». «В промышленности получение стали осуществляется тремя способами: кислородно-конверторным, мартеновским и в электропечах». Неправильным является такое деление: «Транспорт делится на наземный, водный, воздушный, транспорт общего пользования, транспорт личного пользования», — ибо допущена ошибка «подмена основания», т. е. деление произведено не по одному основанию. Сначала в качестве основания деления берется вид среды, в которой осуществляются перевозки, а затем за основание деления берется назначение транспорта. 3. Члены деления должны исключать друг друга, т. е. не иметь общих элементов, быть соподчиненными понятиями, объемы которых не пересекаются. Это правило тесно связано с предыдущим, так как если деление осуществляется не по одному основанию, то члены деления не будут исключать друг друга. Примеры ошибочных делений: «Дроби бывают десятичными, правильными, неправильными, периодическими, непериодическими»; «Войны бывают справедливыми, несправедливыми, освободительными, захватническими, мировыми»; «Треугольники бывают прямоугольными, тупоугольными, остроугольными, равнобедренными, подобными». В этих примерах члены деления не исключают друг друга. Это следствие допущенной ошибки смешения различных оснований деления. 4. Деление должно быть непрерывным, т. е. нельзя делать скачки в делении. Будет допущена ошибка, если мы скажем: «Сказуемые делятся на простые, на составные глагольные и составные именные». Правильным будет сначала раздели
|
||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 1057; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.120.131 (0.021 с.) |

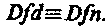 Это правило часто нарушается, в результате,
Это правило часто нарушается, в результате,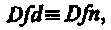 в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.
в неявных определениях просто на место Dfn подставляется контекст, или набор аксиом, или описание способа построения определяемого объекта.