
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация функций выбора
Обозначим S - множество всех возможных функций выбора. Простейшая классификация различает следующие подмножества S: а) S >0 – подмножество функций непустого выбора, т.е. таких функций, выбор по которым содержит хотя бы один элемент; б) S1 – подмножество функций однозначного выбора, т.е. таких функций, выбор по которым содержит ровно один элемент. Ясно, что S1 Í S >0 Í S. Приведем без доказательства следующие теоремы о функциях выбора. ТЕОРЕМА 1. Бинарное отношение R порождает функцию непустого выбора, основанную на механизме доминирования или блокировки тогда и только тогда, когда R ациклично. ТЕОРЕМА 2. Бинарное отношение R порождает функцию однозначного выбора, основанную на механизме доминирования или блокировки тогда и только тогда, когда R ациклично и слабополно. Более тонкая классификация функций выбора основывается на наличии или отсутствии у них следующих свойств. 1) H: (Y Í X) Þ C(X) Ç Y Í C(Y) – свойство наследования. Наличие этого свойства означает, что элемент b, выбираемый на множестве Х, будет также выбран на любом более узком содержащем его подмножестве Y. Иными словами, при переходе к рассмотрению элемента b на более узком множестве, его свойство быть выбранным сохраняется (наследуется). 2) C: X = Y È Z Þ(C(Y) Ç C(Z)) Ì C(X) – свойство согласия. Наличие этого свойства означает, что элемент b, выбираемый одновременно на любых составных частях некоторого множества Х, будет также выбран на всем Х. 3) О: (C(X) Í Y Í X) Þ (C(Y) = C(X)) – свойство отбрасывания или независимости от отбрасывания отвергнутых вариантов. Оно означает, что выбор на любом множестве Y, содержащем выбор C(X) совпадает с C(X). Т.е. выбор не зависит от того, сколько "плохих" элементов пришлось отбросить при выборе. 4) K: (Y Í X) Þ (C(Y) = YÇ (X)) – свойство строгого нас-ледования (константности). Перечислим ряд закономерностей, которые вытекают из названных свойств функций выбора. Пусть (H), (C), (O), (K) Ì S – множества функций выбора, удовлетворяющих соответствующим свойствам. ТЕОРЕМА 3. (K) Ì (H) Ç (C) Ç (O). Т.е. если функция выбора обладает свойством K, то она обладает одновременно свойствами H, C, O. ТЕОРЕМА 4. Для того чтобы функции выбора порождалась бинарным отношением R посредством механизма доминирования или блокировки, необходимо и достаточно, чтобы она принадлежала области (H) Ç (С).
ТЕОРЕМА 5. Для того чтобы функция выбора порождалась качественным порядком необходимо и достаточно, чтобы она принадлежала области (H) Ç (С) Ç (O). ТЕОРЕМА 6. Для того чтобы функция выбора порождалась слабым порядком необходимо и достаточно, чтобы она принадлежала области (К). Свойства Н, С, О кажутся очень естественными при выборе. Тем не менее, несложно привести пример, когда эти свойства не выполняются. Пусть Х – множество точек на плоскости ограниченных прямоугольником АBCD: A(0, 0), B(0, 4), C(2, 4), D(2,0) Ставится следующая задача выбора: на множестве Х найти геометрическое место центров кругов, включенных в Х, максимального радиуса. Покажем что соответствующая функция выбора не обладает ни одним из свойств H, K, O, C. 1) Пусть Х = АBCD; Y = АEFD; E(0,2), F(2,2) (Рис. 1). Тогда множеством центров кругов максимального радиуса, вписанных в ABCD, яввляется отрезок PQ (C(X) = PQ), где P(1, 3), Q(1, 1). Тогда C(X) Ç Y = QR. Очевидно, что C(Y) = Q. Получили, что на множестве X нашлось такое подмножество Y, что хотя YÌ X, тем не менее множество YÇ C(Х) не включено в C(Y), т.е нарушаются условия H и K.
2) Пусть Y = MNOT: M(0, 1), N(0, 3), O(2, 3), T(2, 1) (Рис. 2). Так как, по прежнему, C(X) = PQ, а C(Y) = R(3, 3), то C(X) Ì Y Ì X. Равенство C(X) = C(Y) при этом не выполняется, т.е нарушается условие O. КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ 1. Придумать для рассмотренного выше примера такие множества Y и Z, чтобы нарушалось условие С. 2. Пусть на элементах множества Х задана векторная функция F(x) = { f 1(x), f 2(x),..., f n(x) }. Механизм голосования определяется так: если f i (х) > f i(y), то i-й избиратель голосует за кандидата х против кандидата у. Записать выражение для функции выбора, соответствующей механизму выбора по большинству голосов. 3. Записать функцию выбора, соответствующую механизму блокирующих ограничений, т.е. выбирается элемент х, если он не хуже фиксированного элемента u в смысле бинарного отношения R. 4. На множестве Х = {1, 2,... 5} задано бинарное отношение R с помощью матрицы [R]: [R] = Построить на Х выбор согласно механизмам:
а) доминирования по R; б) блокировки по R; в) блокирующих ограничений при u = 5; г) турнирному. 5. Пусть GR(х) и HR(х) – соответственно верхний и нижний срез отношения R в точке х; |GR(х)| и |HR(х)| – их мощности. Построить выбор на множестве Х = {2, 3,..., 15} согласно следующим механизмам: 1) C1(X) = { xÎХ | max |HR(х)| }; 2) C2(X) = { xÎХ | min |GR(х)| }. Отношение R определяется условиями: а) 6. Доказать, что для любого асимметричного отношения R выполняется включение СR(Х) Í СR(Х). Привести пример, когда это включение строгое. Показать, что условие асимметричности, вообще говоря, не является необходимым, т.е. из СR(Х) Í CR(X) не следует асимметричность R. 7*. Доказать, что для функции выбора, заданной на предъявлении Х и определяемой скалярным максимизирующим механизмом, выполняются следующие условия: а) " x, y Î C(X) f(x) = f(y) = f max; б) " z Î X\C(X) f(z) < f max. 8*. Доказать, что функция выбора, определяемая скалярным оптимизирующим механизмом удовлетворяет условию константности. 9*. Доказать, что если функция выбора на конечном множестве А определяется механизмом блокировки по асимметричному транзитивному бинарному отношению R, то " х Î А\ CR(A) $ y Î CR(A): (y, x) Î R. Иными словами, для любого элемента х, не попавшего в выбор, существует элемент y, лучший, чем х, в смысле отношения R. 10. Составить программу, реализующую метод сканирования, и построить выбор на множестве точек плоскости с целочисленными координатами в соответствии с условно-экстремальным механизмом при следующих условиях. а) f 0 = 2x12 + x22 – 2x1x2 + 6x1 – 11x2 ® min 0 £ x1 £ 6; 0 £ x2 £ 7; x12 + (x2 – 7)2 £ 36. б) f 0 = 2x12 + x22 – 2x1x2 – 4x1 – 6x2 ® min 0 £ x £ 9; 0 £ x2 £ 4; x12 + (x2 – 4)2 £ 81. Примеры решения Задача 7. Выберем два произвольных элемента x,y ÎС(Х). Очевидно, что f(x) = f(y). В противном случае, например при f(x) > f(y), оптимальным был бы элемент х, а y – не был. Поскольку множество С(Х) состоит из элементов, доставляющих максимум f, то в этом случае элемент y не попал бы в выбор С(Х). Условие а) доказано. Для доказательства условия б) введем на множестве Х бинарное отношение I: xIy Û f(x) = f(y). Нетрудно убедиться, что отношение I – эквивалентность. Следовательно, множество Х можно разбить на классы эквивалентности, на которых функция f постоянна. По доказанному условию а), выбор С(Х) целиком содержится в одном из таких классов. Выберем произвольный элемент zÎX \ C(X). В силу определения С(Х), f(z) £ f(x), где х – произвольный элемент С(Х). Но равенства быть не может, т.к. в этом случае, в силу произволь-ности z, все множество Х состояло бы из одного-единственного класса эквивалентности и f(x) была бы постоянна на нем. Ясно, что такого быть не может. Полученное противоречие доказывает условие б). Задача 9. Предположим противное, т.е. существует такой х Î А\ CR (А), что (y, x) Ï R для любого y Î CR(А). Тогда либо х Î CR(А), что невозможно по предположению, либо существует такой z1 Î А\ CR(А), что (z1, x) Î R. Т.е. если элемент х не доминируется никаким элементом из CR(А), то он должен доминироваться некоторым z1 из А\CR(А). В противном случае получим, что х Î CR(А), а это противоречит предположению. Но, в свою очередь, z1 должен доминироваться либо некоторым z2 Î А\CR(А), либо некоторым t Î CR(А), так как иначе получим z1 Î CR(A), что невозможно в силу определения z1. Если верно второе предположение, то, в силу транзитивности R, х доминируется элементом t из множества CR(А), что невозможно. Следовательно, верно первое предположение о существовании z2 Î А\CR(А).
Продолжая эти рассуждения, получим последовательность точек zi Î A\CR(А), таких, что zi R zi -1 и ни одна из них не доминируется никакой точкой из CR(А), т.к. иначе, вследствие транзитивности R, получится, что х доминируется элементом CR(А), что невозможно по предположению. Поскольку R асимметрично и транзитивно, то оно и ациклично. Значит, в этой последовательности не может быть повторяющихся элементов. Поэтому, в силу конечности A, последовательность должна оборваться на элементе zn Î А\CR(А), для которого уже не найдется доминирующего элемента множества А\CR(А). Но он не может доминироваться и элементом CR(А), так как тогда вследствие транзитивности R получим, что и x доминируется этим элементом. Значит, zn недоминируем на A и, следовательно, должен принадлежать CR(А), что противоречит условию zn Î А\CR(А). Полученное противоречие доказывает утверждение задачи.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.240.61 (0.018 с.) |



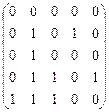
 б)
б) 



