Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование движения небесных тел и заряженных частиц
Движение небесных тел. Рассмотрим модель движения космического тела (планеты, кометы, спутника) под действием силы всемирного тяготения в гравитационном поле, создаваемом телом с многократно большей массой. Входные параметры модели: • масса «большого» тела; • начальные координаты «малого» тела, движение которого изучается; • начальная скорость «малого» тела. В системе координат, начало которой привязано к «большому» телу, дифференциальные уравнения модели имеют вид:
Они получаются из второго закона Ньютона и закона всемирного тяготения. G = 6,67 10ֿ¹¹ м3/кг с2 — гравитационная постоянная. Движение заряженных частиц. Рассмотрим модель движения заряженной частицы в кулоновском поле другой заряженной частицы, положение которой фиксировано. Входные параметры модели: • q к Q - соответственно заряды движущейся и закрепленной частиц; • т - масса движущейся частицы; • начальные координаты движущейся частицы; • начальная скорость движущейся частицы. В системе координат, начало которой привязано к «большому» телу, дифференциальные уравнения модели имеют вид
Эти уравнения получаются из второго закона Ньютона и закона Кулона; ε0 =0,85*10-12 Ф/м - электрическая постоянная. Знак «минус» в двух последних уравнениях соответствует разноименно заряженным частицам; в случае одноименных зарядов он меняется на «плюс». Взаимные движения разноименно заряженных частиц и движения двух небесных тел качественно очень схожи (это становится совершенно очевидным после обезразмеривания уравнений (13) и (14)). Контрольные вопросы 1. Как формулируется закон всемирного тяготения? 2. Как формулируется закон Кулона? Тема для рефератов Движение небесных тел. Задача двух тел. Возмущения. Задача трех тел. Темы семинарских занятий 1. Движение небесных тел. Закон всемирного тяготения. Законы Кеплера. 2. Закон Кулона. Единицы измерения электрических величин. Характеристики электрического поля. Лабораторная работа Общие рекомендации 1. Целесообразно до начала компьютерной реализации модели провести обезразмеривание переменных, входящих в уравнения, выявить безразмерные комбинации параметров модели и дальнейшие действия производить в безразмерных величинах.
2. Необходим контроль точности результатов и устойчивости применяемого численного метода. Для этого достаточно ограничиться эмпирическими приемами (например, сопоставлением решений, полученных с несколькими разными шагами по времени). 3. Целесообразно применять для моделирования стандартные методы интегрирования систем дифференциальных уравнений, описанные в математической литературе. Простейшие методы (метод Эйлера) часто бывают неустойчивы, и их применение ведет к лишнему расходу времени. 4. Результаты моделирования следует выводить на экран компьютера в следующем виде: в виде таблиц зависимостей перемещения и скорости от времени, в виде графиков этих зависимостей, в виде траекторий. Желательны динамические иллюстрации движения тел (скажем, изображение движения по траекториям в некотором условном масштабе времени через равные промежутки). Уместны звуковые сигналы (одни - в критические моменты для моделируемого движения, другие - через каждый фиксированный отрезок пройденного пути и т.д.). 5. При выводе результатов в табличном виде следует учитывать, что соответствующий шаг по времени не имеет практически ничего общего с шагом интегрирования и определяется удобством и достаточной полнотой для восприятия результатов на экране. Экран, сплошь забитый числами, зрительно плохо воспринимается. Выводимые числа следует разумным образом форматировать, чтобы незначащие цифры практически отсутствовали. 6. При выводе результатов в графической форме графики должны быть построены так, как это принято в математической литературе (с указанием величин отложенных по осям, их размерности и масштаба и т.д.). 7. Поскольку таблицы, графики и траектории на одном экране обычно не помещаются, удобно сделать меню, в котором пользователь выбирает желаемый в настоящий момент вид представления результатов. Примерное время выполнения 16 часов. Задания к лабораторной работе 1) Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения. 2) Если моделирование будет производиться в безразмерных переменных (решение - на усмотрение студента и преподавателя), то произвести обезразмеривание и найти набор значений безразмерных параметров.
3) Спроектировать пользовательский интерфейс программы моделирования, обращая особое внимание на форму представления результатов. 4) Выбрать метод интегрирования системы дифференциальных уравнений модели, найти в библиотеке стандартных программ или разработать самостоятельно программу интегрирования с заданной точностью. 5) Произвести отладку и тестирование полной программы. 6) Выполнить конкретное задание из своего варианта работы. 7) Качественно проанализировать результаты моделирования. 8) Создать текстовый отчет по лабораторной работе, включающий:
• титульный лист (название работы, исполнителя, группу и т.д.); • постановку задачи и описание модели; • результаты тестирования программы; • результаты, полученные в ходе выполнения задания (в различной форме); • качественный анализ результатов. Варианты заданий Вариант 1 Найти траекторию полета кометы, залетевшей в Солнечную систему, у которой на расстоянии от Солнца 100 астрономических единиц (1 а.е. = 1,50 * 1011 м расстояние от Земли до Солнца) скорость (ν = 10 км/с) направлена под углом α = 30° к оси «комета - Солнце». Является ли эта траектория замкнутой? Если «да», то сколько длится для нее период полета? Вариант 2 В условиях предыдущей задачи подобрать то значение угла а, при котором траектория из незамкнутой превращается в замкнутую (скорость ν фиксирована). Вариант 3 Вусловиях задачи из варианта 1 подобрать то значение скорости ν, при котором траектория из незамкнутой превращается в замкнутую (угол αфиксирован). Вариант 4 Проверить в компьютерном эксперименте выполнимость второго закона Кеплера, определяющего движение небесных тел по замкнутой траектории. Вариант 5 Проверить в компьютерном эксперименте выполнимость третьего закона Кеплера, определяющего движение небесных тел по замкнутой траектории. Вариант 6 Промоделировать траекторию движения малого космического аппарата, запускаемого с борта космической станции, относительно Земли. Запуск осуществляется путем толчка в направлении, противоположном движению станции, по касательной к ее орбите. Вариант 7 Промоделировать траекторию движения малого космического аппарата, запускаемого с борта космической станции, относительно Земли. Запуск осуществляется путем толчка в направлении, перпендикулярном к плоскости орбиты движения станции. Вариант 8 Как будет выглядеть полет искусственного спутника Земли, если учесть возмущающее действие Луны? Вариант 9 Разработать и реализовать модель движения искусственного спутника Земли при учете воздействия на него малой постоянной силы, обусловленной «солнечным ветром». Считать, что плоскость орбиты движения спутника изначально перпендикулярна к «солнечному ветру». Вариант 10 Считая, что движение Луны вокруг Земли происходит практически по круговой орбите, проанализировать воздействие на эту орбиту со стороны Солнца для малого участка движения, на котором плоскость орбиты перпендикулярна к оси «Солнце - Земля». Вариант 11
Проанализировать особенности движения искусственного спутника Земли, движущегося практически по круговой орбите на высоте порядка 300 км, связанные с малым сопротивлением атмосферы. Вариант 12 Проанализировать изменение круговой орбиты астероида, движущегося вокруг Солнца, под влиянием вулканического выброса с его поверхности. Вариант 13 Найти траекторию движения тела массой 1 г, несущего заряд величиной q = 1 • 10-2 К, в поле заряда величиной Q= 5 • 10-2 К. Начальное расстояние между зарядами 1 м, начальная скорость равна 1 • 10-1 м/с и направлена под углом 30° к оси, соединяющей заряды. Провести моделирование для случая зарядов одного знака. Вариант 14 В условиях предыдущей задачи провести моделирование для случая зарядов разных знаков. Вариант 15 Разработать модель движения практически невесомой заряженной частицы в электрическом поле, созданном системой нескольких фиксированных в пространстве заряженных тел, в случае когда заряженные тела находятся в одной плоскости и в ней же находится движущаяся частица. Вариант 16 То же, что и в предыдущем варианте, но частица находится вне плоскости расположения зарядов; ее начальная скорость перпендикулярна к этой плоскости. Вариант 17 Имеется неподвижная заряженная частица с зарядом Q и экран (рис. 2). В точке А экрана находится мишень. При каких соотношениях величины начальной скорости ν0 движущейся частицы (заряд q) и угла прицеливания α она попадет в мишень? Расстояния обозначены на рисунке. Заряды частиц - разных знаков.
Рис. 2. К задаче варианта 17 Вариант 18 То же условие, что и в предыдущей задаче, но расположение частиц и экрана соответствует рис. 3; заряды частиц имеют одинаковые знаки.
Рис. 3. К задаче варианта 18 Вариант 19 Промоделировать движение заряженной частицы между пластинами плоского конденсатора. Поле конденсатора считать однородным, начальная скорость частицы направлена параллельно пластинам. Частицу считать практически невесомой. Вариант 20 Промоделировать движение легкого (практически невесомого) заряженного тела сферической формы между горизонтальными пластинами плоского конденсатора с учетом сопротивления воздуха, находящегося между пластинами. Вариант 21 Легкая заряженная частица падает вертикально вниз (под влиянием силы тяжести) на одноименно заряженную пластину (начальная скорость обеспечивает движение вниз независимо от соотношения силы тяжести и силы электростатического отталкивания). Промоделировать движение частицы, считая поле, созданное пластиной, однородным.
Вариант 22 Легкая заряженная частица влетает в однородное поле, созданное горизонтально расположенными пластинами конденсатора. Промоделировать ее траекторию, учитывая силу тяжести и электростатическую силу. Вариант 23 Тоже, что и в предыдущем варианте, но пластины конденсатора расположены вертикально. Вариант 24 То же, что и в варианте 22, то пластины конденсатора расположены наклонно. Дополнительная литература 1. ГулдХ., ТобочникЯ. Компьютерное моделирование в физике: Пер. с англ. Т. 1,2. - М.: Мир, 1990. 2. Калашников С.Г. Электричество. - М.: Наука, 1977. 3. Левантовский В.И. Механика космического полета. М.: Наука, 1970. 4. Савельев И.В. Курс общей физики: В 3 т. Т. 1,2. - М.: Наука, 1977. 5. Сивухин Д.В. Общий курс физики: В 5 т. Т. 1, 3, 5. - М.: Наука, 1974. 6. Стрелков СП. Механика. - М.: Наука, 1975. 7. Хайкин С.Э. Физические основы механики. - М.: Наука, 1976. Краткие сведения Колебательные процессы Рассмотрим модель движения математического маятника (рис. 4) при произвольном (не малом) начальном угле отклонения. Поскольку нить подвеса считается нерастяжимой, то у маятника одна степень свободы. Удобно принять за нее угол между нитью подвеса и вертикалью. Уравнения движения имеют вид
Рис 4. Математический маятник В случае малых колебаний (колебаний с малой амплитудой) оно превращается в так называемое уравнение малых колебаний, отличающееся от полного заменой в правой части sin(θ) на θ. Задача о малых колебаниях имеет простое аналитическое решение θ=A cos (ωt + φ) (16) где А - амплитуда колебаний, ω - частота, φ - начальная фаза. А и φ можно выразить через начальные условия - угол θ0 и скорость v 0:
Частота колебаний Малые колебания маятника - пример так называемого гармонического движения, описываемого простой тригонометрической функцией (см. (16)). Для численного эксперимента удобно представить уравнение колебаний в форме системы двух уравнений первого порядка:
Входные параметры модели: l - длина нити подвеса;
х0 - начальная угловая скорость. Колебания маятника с трением в точке подвеса описываются следующим уравнением:
где, как и выше, Уравнение (19а) равносильно системе уравнений
Трение приводит, в частности, к тому, что в зависимости от соотношения η и ω появляются разные режимы движения: затухающие колебания и затухание без колебаний. Одна из задач исследования - найти на фазовой плоскости (η, ω) зависимость линии, разделяющей два режима, от начального отклонения маятника. Входные параметры модели: ω - частота собственных малых колебаний маятника;
θ0 - начальное отклонение маятника; х0 - начальная угловая скорость; η - коэффициент трения. Вынужденные колебания маятника описываются уравнением
где f - амплитуда, λ - частота вынуждающей силы. Уравнение (20а) равносильно системе уравнений
При Вынужденные колебания характеризуются двумя этапами - переходным процессом и стационарными колебаниями с частотой вынуждающей силы. При Входные параметры модели: ω - частота собственных малых колебаний маятника; θ0 - начальное отклонение маятника; х0 — начальная угловая скорость; η - коэффициент трения; f - амплитуда вынуждающей силы; λ - частота вынуждающей силы. При периодическом изменении длины нити подвеса уравнение колебаний принимает вид
где λ - частота колебаний нити подвеса. Уравнение (7.21а) равносильно системе уравнений
Одно из принципиальных явлений, связанных с этими колебаниями, — появление так называемого параметрического резонанса при некоторых соотношениях частот λи ω0:
Входные параметры модели: ω0 - частота собственных малых колебаний маятника; θО - начальное отклонение маятника; х0 - начальная угловая скорость; η - коэффициент трения; α - амплитуда модуляции; λ - частота модуляции. Контрольные вопросы 1. Как выглядят математические модели следующих движений: • колебаний математического маятника без трения; • малых колебаний математического маятника без трения; • колебаний математического маятника с трением; • вынужденных колебаний математического маятника; • параметрически возбуждаемых колебаний математического маятника? 2. Как качественно влияет наличие трения на вид колебаний? Являются ли соответствующие колебания гармоническими? 3. В чем заключается процедура Фурье-анализа периодических процессов? Темы для рефератов 1. Маятники различных видов. Свободные, вынужденные и параметрические колебания. 2. Спектральный анализ периодических процессов. 3. Колебания пружинного маятника. 4. Колебания крутильного маятника. Тема семинарских занятий Гармонические колебания. Спектральный анализ периодических процессов. Лабораторная работа Общие рекомендации 1. Целесообразно до начала компьютерной реализации модели провести обезразмеривание переменных, входящих в уравнения, выявить безразмерные комбинации параметров модели и дальнейшие действия производить в безразмерных величинах. 2. Необходим контроль точности результатов и устойчивости применяемого численного метода. Для этого достаточно ограничиться эмпирическими приемами (например, сопоставлением решений, полученных с несколькими разными шагами по времени). 3. Целесообразно применять для моделирования стандартные методы интегрирования систем дифференциальных уравнений, описанные в математической литературе. Простейшие методы (метод Эйлера) часто бывают неустойчивы, и их применение ведет к лишнему расходу времени. 4. Результаты моделирования следует выводить на экран компьютера в следующем виде: в виде таблиц зависимостей перемещения и скорости от времени, в виде графиков этих зависимостей, в виде траекторий. Желательны динамические иллюстрации движения тел (скажем, изображение движений по траекториям в некотором условном масштабе времени через равные промежутки). Уместны звуковые сигналы (одни - в критические моменты для моделируемого движения, другие - через каждый фиксированный отрезок пройденного пути и т.д.). 5. При выводе результатов в табличном виде следует учитывать, что соответствующий шаг по времени не имеет практически ничего общего с шагом интегрирования и определяется удобством и достаточной полнотой для восприятия результатов на экране. Экран, сплошь забитый числами, зрительно плохо воспринимается. Выводимые числа следует разумным образом форматировать, чтобы незначащие цифры практически отсутствовали. 6. При выводе результатов в графической форме графики должны быть построены так, как это принято в математической литературе (с указанием величин, отложенных по осям, их размерности и масштаба и т.д.). 7. Поскольку таблицы, графики и траектории на одном экране обычно не помещаются, удобно сделать меню, в котором пользователь выбирает желаемый в настоящий момент вид представления результатов. Примерное время выполнения 16 часов. Задания к лабораторной работе 1) Выписать математическую модель, определить состав набора входных параметров и их конкретные числовые значения. 2) Если моделирование будет производиться в безразмерных переменных (решение - на усмотрение студента и преподавателя), произвести обезразмеривание и найти набор значений безразмерных параметров. 3) Спроектировать пользовательский интерфейс программы моделирования, обращая особое внимание на формы представления результатов. 4) Выбрать метод интегрирования системы дифференциальных уравнений модели, найти в библиотеке стандартных программ или разработать самостоятельно программу интегрирования с заданной точностью. 5) Произвести отладку и тестирование полной программы. 6) Выполнить конкретное задание из своего варианта работы. 7) Качественно проанализировать результаты моделирования. 8) Создать текстовый отчет по лабораторной работе, включающий: • титульный лист (название работы, исполнителя, группу и т.д.); • постановку задачи и описание модели; • результаты тестирования программы; • результаты, полученные в ходе выполнения задания (в различных формах); • качественный анализ результатов. Варианты заданий Вариант 1 Установить зависимость периода колебаний маятника T от начальной амплитуды в диапазоне амплитуд θ0є [0, π] и его отклонение от периода малых колебаний Т0. Вариант 2 Установить зависимость периода колебаний маятника T от длины нити подвеса при амплитуде колебаний, равной π/2. Вариант 3 Ограничиваясь тремя членами ряда Фурье, исследовать зависимость амплитуд гармоник а1, а2 и а3 от начальной амплитуды колебаний. Вариант 4 Ограничиваясь тремя членами ряда Фурье, исследовать зависимость амплитуд гармоник а1, а2, и a3 отдлины нити подвеса при амплитуде колебаний, равной π/2. Вариант 5 Заменить в (19) sin(θ) на θ и изучить, как трение влияет на малые колебания математического маятника. Фиксировать параметр l и найти то критическое значение коэффициента трения η*, при котором движение перестает быть колебательным и становится монотонно затухающим (апериодический режим). Вариант 6 В условиях предыдущей задачи построить зависимость η* от l при фиксированном значении ω. Вариант 7 Изучить, как значение начальной амплитуды немалых колебаний математического маятника с трением сказывается на переходе режима затухающих колебаний в режим затухания без колебаний. Вариант 8 Построить зависимость амплитуды малых колебаний без трения от частоты вынуждающей силы λ при приближении ее к частоте собственных колебаний ω0. Вариант 9 Построить зависимость амплитуды немалых колебаний маятника без трения от частоты вынуждающей силы λ при приближении ее к частоте собственных колебаний ω0. Вариант 10 Построить зависимость амплитуды немалых колебаний маятника без трения от амплитуды вынуждающей силы при ее частоте, приблизительно равной половине частоты собственных колебаний маятника. Вариант 11 Получить картину процесса биений в системе с близкими значениями частот λ, иω0 (в приближении малых колебаний и без наличия трения). Вариант 12 Получить картину процесса биений в системе с близкими значениями частот λ и ω0 (для амплитуды колебаний, равной π/2, и без наличия трения). Вариант 13 Исследовать, как возрастание коэффициента трения влияет на процесс биений в системе с близкими значениями частот λ и ω0 (для произвольной амплитуды колебаний). Вариант 14 Исследовать колебания маятника с периодически меняющейся длиной нити подвеса. Построить на фазовой плоскости (λ/ω0, α) границы нескольких зон параметрического резонанса (без учета трения). Вариант 15 В условиях задания из предыдущего варианта исследовать влияние трения на границы нескольких зон параметрического резонанса. Вариант 16 Построить модель колебаний шарика массы т, висящего на пружинке (пружинного маятника), движущегося под влиянием силы тяжести и упругой силы, без учета трения. Исследовать зависимость периода колебаний маятника от длины l при фиксированном значении параметров т и k (жесткости пружины). Вариант 17 Для маятника, описанного в предыдущей задаче, исследовать зависимость периода колебаний от массы при фиксированных значениях параметров k и l. Вариант 18 Для маятника, описанного в варианте 16, добавить учет сопротивления окружающей среды (при конечном размере шарика) и исследовать зависимость периода колебаний от вязкости среды при движении маятника в воде (значения остальных параметров фиксировать). Найти границу перехода периодического движения в апериодическое. Вариант 19 Для маятника, описанного в варианте 16, добавить учет воздействия периодической вынуждающей силы и исследовать зависимость амплитуды колебаний от частоты вынуждающей силы при прохождении через резонанс (без учета трения). Вариант 20 Построить модель колебаний шарика массы т, лежащего на горизонтальной поверхности, под действием пружины, создающей упругую силу Fynp = -ах - bх3, где х - смещение из положения равновесия. Трения не учитывать. Исследовать зависимость периода колебаний такого маятника от параметра b (при фиксированном значении других параметров). Вариант 21 Для маятника, описанного в предыдущем варианте, добавить учет трения шарика о поверхность (сила трения пропорциональна весу шарика) и исследовать зависимость периода колебаний от коэффициента трения. Найти границу перехода периодического движения в апериодическое. Вариант 22 Для маятника, описанного в варианте 20, добавить учет наличия вынуждающей периодической силы и исследовать зависимость периода колебаний от амплитуды вынуждающей силы при ее частоте, равной приблизительно половине частоты собственных колебаний (без учета трения). Вариант 23 Для маятника, описанного в варианте 20, добавить учет наличия вынуждающей периодической силы и исследовать зависимость периода колебаний от частоты вынуждающей силы при прохождении через резонанс (без учета трения). Вариант 24 Исследовать процесс биений для маятника, описанного в варианте 20, в отсутствии трения. Дополнительная литература 1. Мигулин В. В. и др. Основы теории колебаний. - М.: Наука, 1988. 2. Савельев И. В. Курс общей физики: В 3 т. Т. 1, 2. - М.: Наука, 1977. 3. СивухинД. В. Общий курс физики: В 5 т. Т. 1. - М.: Наука, 1974. 4. Стрелков СП. Механика. - М.: Наука, 1975. 5. Стрелков СП. Введение в теорию колебаний. - М.: Наука, 1964. 6. Хайкин С.Э. Физические основы механики. - М.: Наука, 1976. Краткие сведения
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.96.254 (0.132 с.) |
 (13)
(13) (14)
(14)

 (15)
(15)
 (17)
(17) отметим, что она, равно как и период колебаний
отметим, что она, равно как и период колебаний  , в приближении малых колебаний не зависит от начальной амплитуды.
, в приближении малых колебаний не зависит от начальной амплитуды. (18)
(18)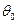 - начальное отклонение маятника;
- начальное отклонение маятника; (19а)
(19а) - коэффициент трения.
- коэффициент трения.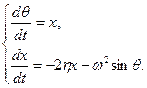 (19б)
(19б) (20а)
(20а) (20б)
(20б) наступает резкое возрастание амплитуды вынужденных колебаний. При
наступает резкое возрастание амплитуды вынужденных колебаний. При  эта амплитуда в приближении малых колебаний формально бесконечна, однако само приближение при этом не работает.
эта амплитуда в приближении малых колебаний формально бесконечна, однако само приближение при этом не работает. (21а)
(21а)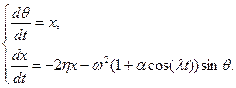 (21б)
(21б)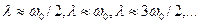 .
.