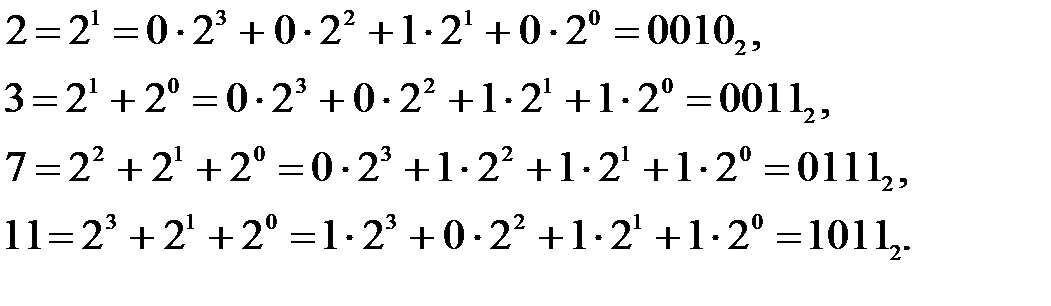Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекуррентные соотношения. Возвратные последовательности
Рекуррентным соотношением называется соотношение вида Пример 2.11. Формула Последовательность Пример 2.12. Геометрическая прогрессия – это возвратная последовательность, так как Многочлен Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением. Описание общего решения имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами. Пусть l – корень характеристического уравнения. Тогда общее решение рекуррентного соотношения можно найти следующим образом: 1. если li – корень кратности 1 (i =1,…, k), то общее решение имеет вид 2. если li – корень кратности ri (i =1,…, k), то общее решение имеет вид Зная общее решение рекуррентного соотношения, по начальным условиям можно найти неопределенные постоянные и тем самым получить частное решение рекуррентного уравнения с данными начальными условиями. Пример 2.13. Найти последовательность { an }, удовлетворяющую рекуррентному соотношению Составим характеристический многочлен Для нахождения корней сгруппируем слагаемые Составим характеристическое уравнение
решая которую находим с1 =1, с2 = 1, с3 =1. Таким образом, Алгебра логики Булевы функции Функцией алгебры логики или булевой функцией называется функция n переменных Булева функция
Рассмотрим булевы функции одного аргумента. Эти функции определены на двух наборах. Приведем обозначения и названия этих функций.
Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Функция f 1 называется тождественной функцией и обозначается через x. Функция f 2 называется отрицанием x и обозначается Рассмотрим часто используемые булевы функции двух аргументов. Эти функции определены на четырех наборах.
Приведем обозначения и названия этих функций. Функция f 3 называется конъюнкцией x 1 и x 2 и обозначается x 1× x 2. Функция f 4 называется дизъюнкцией x 1 и x 2 и обозначается С помощью операции суперпозиции из этих элементарных функций можно построить функции большего числа аргументов. Заметим, что булеву функцию можно однозначно определить перечислением всех наборов, на которых она принимает значение 1. Функция Булева алгебра Множество булевых функций с операциями
1.
2.
3.
4.
5. `0=1
6.
7. 8. 9.
Если в формуле несколько одинаковых по старшинству операций следуют друг за другом, то они выполняются слева направо. Рассмотрим несколько дополнительных законов булевой алгебры, которые могут быть доказаны с помощью перечисленных выше аксиом и которые часто используются для эквивалентных преобразований. 1. 2. Нормальные формы Булевы функции удобнее задавать в виде формул. Одной функции может соответствовать множество формул, содержащих аргументы функции, знаки дизъюнкции, конъюнкции и отрицания. Элементарной дизъюнкцией называется дизъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза. Пример 3.1. Элементарной конъюнкцией называется конъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза. Пример 3.2. Дизъюнктивной нормальной формой (днф) называется дизъюнкция конечного множества попарно различных элементарных конъюнкций. Пример 3.3. Аналогично, можно определить конъюнктивную нормальную форму (кнф), как конъюнкцию конечного множества попарно различных элементарных дизъюнкций. Пример 3.4. В примере видно, что Для любой функции можно найти ее представление в днф и кнф, используя аксиомы алгебры логики. Пример 3.5. Найти днф, кнф для функции
Любая булева функция может иметь много представлений в виде днф и кнф. Особое место среди этих представлений занимают совершенные днф (сднф) и совершенные кнф (скнф). Конституентой единицы k1 набора Пример 3.6. Построим СДНФ и СКНФ для функции f, для которой задана таблица истинности.
Для построения СДНФ рассмотрим все наборы, на которых функция принимает значение 1, и выпишем для этих наборов все k1:
Тогда СДНФ имеет вид:
Для построения СКНФ рассмотрим все наборы, на которых функция принимает значения 0, и выпишем для этих наборов k0:
Тогда СКНФ имеет вид:
Для построения СДНФ из ДНФ можно домножить элементарную конъюнкцию на
Пример 3.7. Найти СДНФ для функции
Для построения СКНФ из КНФ в элементарную дизъюнкцию, не содержащую переменную xi, добавляем Пример 3.8. Найти СКНФ для функции В дальнейшем для представления СДНФ функции f будем указывать номера k1, на которых функция равна 1. Для определения набора необходимо перевести номер k1 в двоичное число. Пример 3.9. Пусть СДНФ функция f определяется следующим образом.
Переведем номера k1 в двоичные числа
Таким образом, f обращается в 1 на наборах (0,0,0,1), (0,1,0,1), (1,0,0,0), (1,0,1,1), (1,1,1,0). Аналогично, для представления функции в СКНФ будем использовать запись с указанием номеров k0, на которых функция равна 0. Пример 3.10. Переведем номера k0 в двоичные числа
Функция f обращается в 0 на наборах (0,0,1,0), (0,0,1,1), (0,1,1,1), (1,0,1,1).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.83.185 (0.039 с.) |
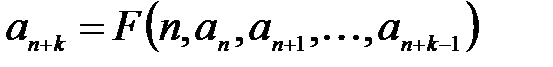 , которое позволяет вычислить все члены последовательности
, которое позволяет вычислить все члены последовательности  , если заданы ее первые k членов.
, если заданы ее первые k членов. задает арифметическую прогрессию.
задает арифметическую прогрессию.
 называется возвратной, если для всех n и некоторого k выполняется
называется возвратной, если для всех n и некоторого k выполняется  где pi = const.
где pi = const.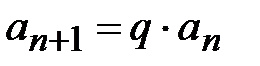 . Следовательно, выполняется
. Следовательно, выполняется 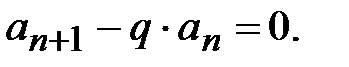
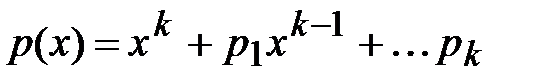 называется характеристическим для возвратной последовательности.
называется характеристическим для возвратной последовательности.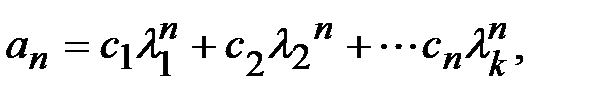 где ci = const (i =1,…, k).
где ci = const (i =1,…, k).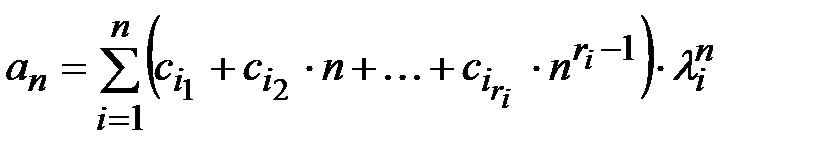 , где
, где  – произвольные константы (i =1,…, n, j =1,…, ri).
– произвольные константы (i =1,…, n, j =1,…, ri).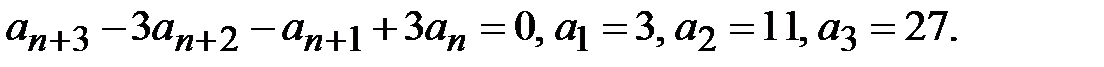

 .
.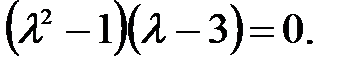 Его корнями являются числа
Его корнями являются числа 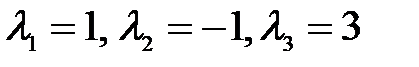 . Следовательно, общее решение рекуррентного соотношения имеет вид:
. Следовательно, общее решение рекуррентного соотношения имеет вид:  . Используя начальные условия, получим систему:
. Используя начальные условия, получим систему:
 .
. если аргументы функции являются булевыми переменными (т.е.
если аргументы функции являются булевыми переменными (т.е. 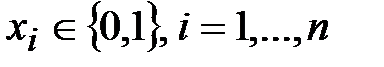 ), и функция может принимать только два значения: 0 или 1. Таким образом, булева функция
), и функция может принимать только два значения: 0 или 1. Таким образом, булева функция 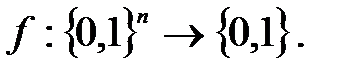 Булевы функции называются также переключательными функциями. Каждая комбинация значений аргументов булевой функции называется набором. Для функции n переменных количество разных наборов равно 2 n.
Булевы функции называются также переключательными функциями. Каждая комбинация значений аргументов булевой функции называется набором. Для функции n переменных количество разных наборов равно 2 n. задается таблицей истинности:
задается таблицей истинности: .
.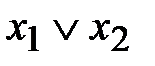 . Функция f 5 называется суммой по модулю 2 и обозначается
. Функция f 5 называется суммой по модулю 2 и обозначается 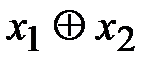 . Функция f 6 называется импликацией и обозначается
. Функция f 6 называется импликацией и обозначается 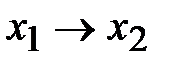 (читается x 1 влечет x 2). Функция f 7 называется эквивалентностью и обозначается x 1 ~ x 2 (читается x 1 эквивалентно x 2). Функция f 8 называется штрихом Шеффера и обозначается x 1 |x 2 (читается не x 1 и x 2).
(читается x 1 влечет x 2). Функция f 7 называется эквивалентностью и обозначается x 1 ~ x 2 (читается x 1 эквивалентно x 2). Функция f 8 называется штрихом Шеффера и обозначается x 1 |x 2 (читается не x 1 и x 2). существенно зависит от переменной xi, если
существенно зависит от переменной xi, если  для любых значений
для любых значений  . В противном случае переменная xi - фиктивная. Наборы, отличающиеся значением только одной переменной xi, называются соседними.
. В противном случае переменная xi - фиктивная. Наборы, отличающиеся значением только одной переменной xi, называются соседними. (дизъюнкция), ×(конъюнкция),
(дизъюнкция), ×(конъюнкция),  (отрицание) называется булевой алгеброй. Операция отрицание имеет самый высокий приоритет, затем идет конъюнкция, а затем дизъюнкция. Рассмотрим основные аксиомы булевой алгебры (в аксиомах x, y, z могут быть булевыми переменными или функциями).
(отрицание) называется булевой алгеброй. Операция отрицание имеет самый высокий приоритет, затем идет конъюнкция, а затем дизъюнкция. Рассмотрим основные аксиомы булевой алгебры (в аксиомах x, y, z могут быть булевыми переменными или функциями).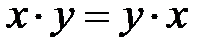
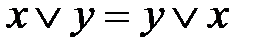 коммутативность
коммутативность
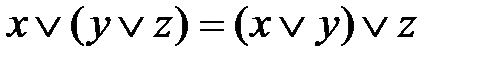 ассоциативность
ассоциативность
 идемпотентность
идемпотентность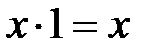

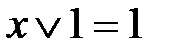
 свойства констант
свойства констант
 аксиомы отрицания
аксиомы отрицания
 дистрибутивность
дистрибутивность закон исключения третьего
закон исключения третьего закон противоречия
закон противоречия
 законы де Моргана
законы де Моргана поглощение
поглощение склеивание
склеивание , x 1
, x 1 ,
, 
 ,
, 
 ,
, 
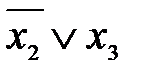 является одновременно днф и кнф.
является одновременно днф и кнф.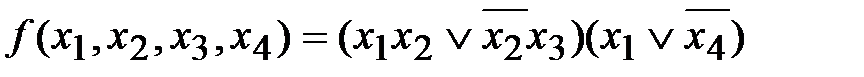
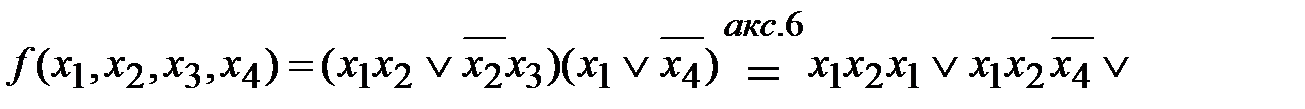
 – Днф.
– Днф.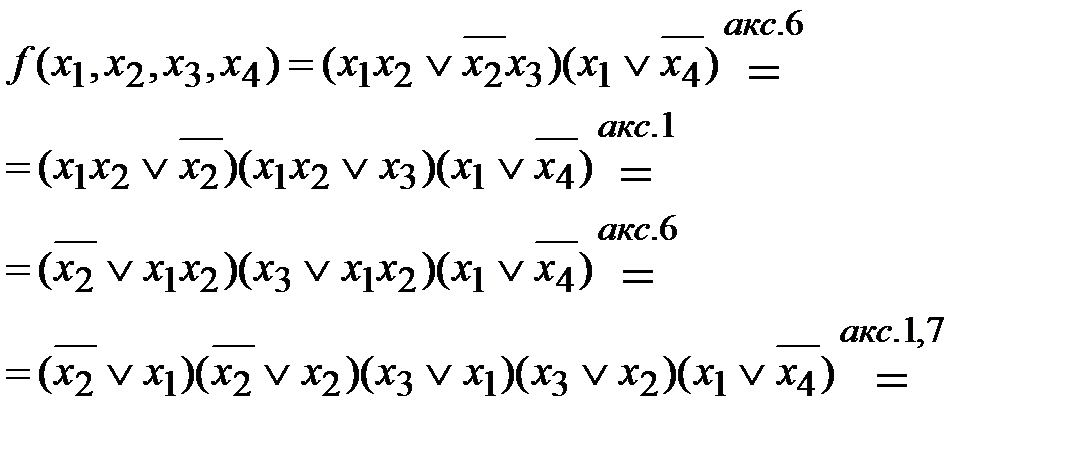
 – кнф.
– кнф. называется конъюнкция всех переменных, образующих этот набор. Причем, переменная входит в конъюнкцию с отрицанием, если она на данном наборе равна 0 и без отрицания, если она равна 1. Конституентой нуля k0 данного набора называется дизъюнкция всех переменных, образующих этот набор. Переменная входит в дизъюнкцию без отрицания, если она на этом наборе равна 0 и с отрицанием, если она равна 1. Совершенная дизъюнктивная нормальная форма функции f – дизъюнкция k1 тех наборов, на которых функция принимает значение 1. Совершенная конъюнктивная нормальная форма функции f – конъюнкция k0 тех наборов, на которых функция принимает значение 0. Представление функции в СДНФ или СКНФ единственно. Совершенные формы легко строить по таблице истинности.
называется конъюнкция всех переменных, образующих этот набор. Причем, переменная входит в конъюнкцию с отрицанием, если она на данном наборе равна 0 и без отрицания, если она равна 1. Конституентой нуля k0 данного набора называется дизъюнкция всех переменных, образующих этот набор. Переменная входит в дизъюнкцию без отрицания, если она на этом наборе равна 0 и с отрицанием, если она равна 1. Совершенная дизъюнктивная нормальная форма функции f – дизъюнкция k1 тех наборов, на которых функция принимает значение 1. Совершенная конъюнктивная нормальная форма функции f – конъюнкция k0 тех наборов, на которых функция принимает значение 0. Представление функции в СДНФ или СКНФ единственно. Совершенные формы легко строить по таблице истинности. ,
,  ,
,  ,
,  .
.
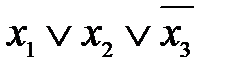 ,
, 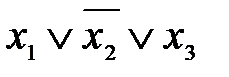 ,
, 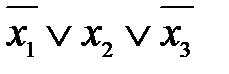 ,
,  .
.
 (если переменная xi отсутствует в элементарной конъюнкции) и применить закон дистрибутивности.
(если переменная xi отсутствует в элементарной конъюнкции) и применить закон дистрибутивности.
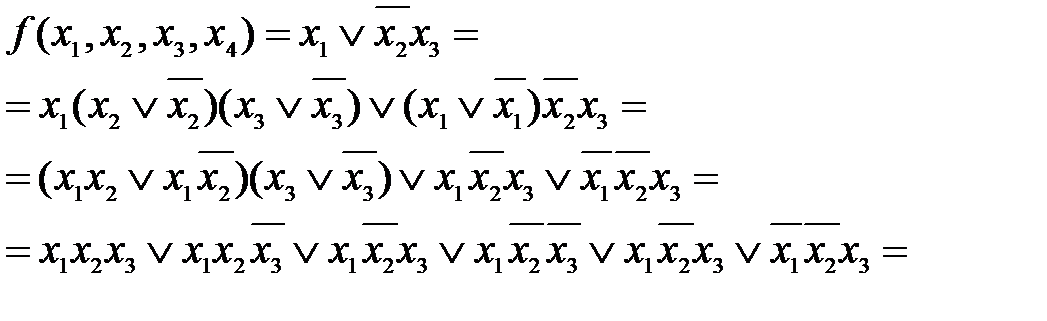
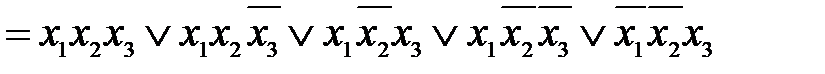 – СДНФ.
– СДНФ. и применяем закон дистрибутивности.
и применяем закон дистрибутивности.

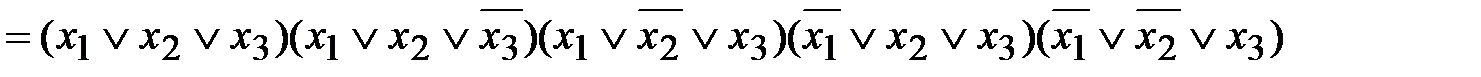 – СКНФ.
– СКНФ. =
= 
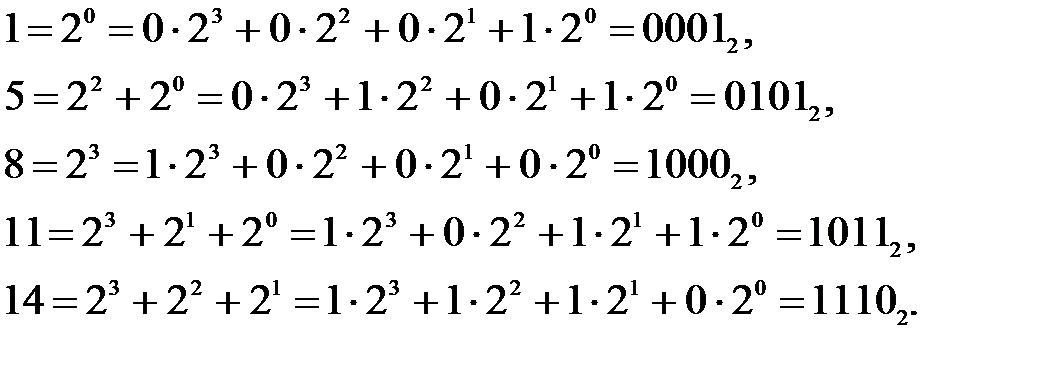
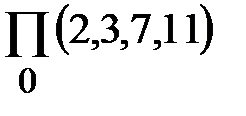 .
.