Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные алгебраические операции над нечеткими множествами и их свойства
n Алгебраическое произведение А и В обозначается определяется функцией принадлежности вида mA B (x) = mA(x) mB(x), " x Î E n Алгебраическая сумма этих множеств обозначается А+В и определяется функцией принадлежности mA+ B (x) = mA(x) + mB(x) — mA(x) mB(x), " x Î E n Степенью нечеткого множества A называется нечеткое множество A α с функцией принадлежности µAα (x) = µαA (x), " x Î E, α>0.
18. Бинарная операция и ее основное множество. Способы задания бинарной операции. Таблица Кэли. Операционный квадрат таблицы Кэли. Группоид. Свойства бинарных алгебраических операций. Бинарная операция — этоотображение множества A ´ A в множество A, при этом образ пары (x, y) обозначим, например, x · y, где · — символ операции. Здесь A — произвольное непустое множество и A ´ A — множество всех упорядоченных пар (x, y) — таких, что x, y Î A. Непустое множество A называется основным множеством операции. Можно составить иерархию множеств с бинарной операцией (разумеется, вместо · может быть вставлена любая: +, –, *, È, Ç, Å, Ä, Ñ, ° и т.д. и т.п.). Свойства бинарных операций · Ассоциативность · Коммутативность · Дистрибутивность слева и справа · Существование нейтрального элемента · Разрешимость уравнений · Существование обратного элемента Таблица Кэли – матрица | ai,aj |, где (
Свойства бинарных алгебраических операций. Квазигруппа. Лупа. Полугруппа. Моноид. Группа. Абелева группа. Свойства бинарных операций · Ассоциативность ((a ° b) ° c = a ° (b ° c)) · Коммутативность (a · b = b · a) · Дистрибутивность слева и справа · Существование нейтрального элемента (a ° e = e ° a = a) · Разрешимость уравнений (a · x = b, y · a = b имеет единственное решение для любых элементов a, b этого множества) · Существование обратного элемента a ° a^ –1= a^ –1° a = e
Группа симметрий фигуры.
Группа симметрий фигуры на плоскости (поворот, отражение вдоль некоторой оси и т.п.) Группу симметрий фигуры образует множество G различных движений плоскости, самосовмещающих данную фигуру. Чем больше множество G, тем симметричнее фигура. Таблица Кэли: композиции движения. Свойства операций: Существование нейтрального элемента; Если есть латинский квадрат (в каждом столбце и каждой строке таблицы встречается каждый из элементов множества), то существует разрешимость уравнений; Ассоциативность.
Группа подстановок. Отображается множество на себя.
Решение:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.157.51 (0.006 с.) |
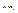 ) – результат операции i элемента на j -ый. Группоид, обозначаемый символом (A, ©) — множество A, на котором задана некоторая бинарная операция, обозначаемая ©. Если множество группоида конечно, ½A½ = n, то таблица операции группоида есть таблица n ´ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Группоид можно считать заданным, если выписана его таблица операции.
) – результат операции i элемента на j -ый. Группоид, обозначаемый символом (A, ©) — множество A, на котором задана некоторая бинарная операция, обозначаемая ©. Если множество группоида конечно, ½A½ = n, то таблица операции группоида есть таблица n ´ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Группоид можно считать заданным, если выписана его таблица операции.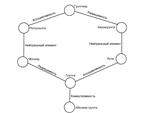
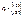 ,
, 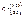 ,
, 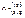 ,
, 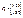 ,
, 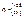
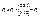 ,
, 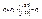 ,
, 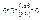 ,
, 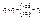 ,
,