Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множества. Отношение принадлежности. Универсум и пустое множество. Мощность множества. Отношение включения. Подмножество, надмножество, собственное подмножество. Булеан множества. Парадокс РасселаСтр 1 из 7Следующая ⇒
Операции над множествами. Диаграммы Эйлера. Покрытия и разбиения. Объединением (дизъюнкцией, суммой) множеств A и B называется множество A È B = { x ï x Î A или x Î B }. Пересечением (конъюнкцией) множеств A и B называется множество A Ç B = { x ï x Î A и x Î B }. Разностью множеств A и B называется множество A \ B = { x ï x Î A и x Ï B } Разность U \ A называется дополнением множества A и обозначается через –A. Симметрической разностью множеств A и B называется множество A % B = (A \ B)È (B \ A) Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В. Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Вэйна. Разбиения и покрытия множеств Если множество A представляет собой объединение подмножеств А1, А2, …, Аn, …, то совокупность {А1, А2, …, Аn, …} подмножеств называется покрытием множества A. Если же совокупность подмножеств покрытия множества A такова, что Ai Ç Aj = Æ при i¹ j, то совокупность {А1, А2, …, Аn, …} называется разбиением множества A, а подмножества Ai — классами этого разбиения.
Основные тождества алгебры множеств. Формула включений и исключений. Идемпотентность: Коммутативность: Ассоциативность: Дистрибутивность: Поглощение: Де Моргана:
Замыкание отношений. Рефлексивное, симметричное, транзитивное замыкание отношений. R* называется замыканием отношения R относительно свойства P, если · R* обладает свойством P; · R Í R*; · R* является подмножеством любого другого отношения, содержащего R и обладающего свойством P. Пусть R — некоторое бинарное отношение на множестве A: · Рефлексивным замыканием R D отношения R называется отношение R È D A. · Симметричным замыканием R S отношения R называется отношение R È R #. · Транзитивным замыканием Rt отношения R называется отношение. Rt = R È R 2 È R 3 È… È Rn È… Если некоторое отношение включает свое симметричное, рефлексивное и транзитивное замыкания, то оно является отношением эквивалентности и наоборот.
Свойства бинарных операций · Ассоциативность · Коммутативность · Дистрибутивность слева и справа · Существование нейтрального элемента
· Разрешимость уравнений · Существование обратного элемента Таблица Кэли – матрица | ai,aj |, где (
Свойства бинарных операций · Ассоциативность ((a ° b) ° c = a ° (b ° c)) · Коммутативность (a · b = b · a) · Дистрибутивность слева и справа · Существование нейтрального элемента (a ° e = e ° a = a) · Разрешимость уравнений (a · x = b, y · a = b имеет единственное решение для любых элементов a, b этого множества) · Существование обратного элемента a ° a^ –1= a^ –1° a = e
Группа симметрий фигуры. Группа симметрий фигуры на плоскости (поворот, отражение вдоль некоторой оси и т.п.) Группу симметрий фигуры образует множество G различных движений плоскости, самосовмещающих данную фигуру. Чем больше множество G, тем симметричнее фигура. Таблица Кэли: композиции движения. Свойства операций: Существование нейтрального элемента; Если есть латинский квадрат (в каждом столбце и каждой строке таблицы встречается каждый из элементов множества), то существует разрешимость уравнений; Ассоциативность.
Группа подстановок. Отображается множество на себя.
Решение:
Граф. Вершина, ребро, дуга. Неориентированный граф, ориентированный граф (орграф). Кратные ребра (дуги). Петли. Смежные вершины, смежные дуги. Степень вершины. Инцидентные ребро и вершина, дуга и вершина. Граф — множество V вершин и набор E неупорядоченных и упорядоченных пар вершин; обычно граф обозначают как G (V, E). Неупорядоченная пара вершин называется ребром, упорядоченная пара — дугой. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги — ориентированным (или орграфом). Пара вершин может быть соединена двумя или более ребрами (или, соответственно, дугами одного направления), такие ребра (или дуги) называются кратными. Дуга (или ребро) может начинаться и заканчиваться в одной и той же вершине. В этом случае соотв. дуга (или ребро) называется петлей. Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие общую вершину, тоже называются смежными. Степень вершины – количество рёбер, выходящих из вершины. Ребро (или дуга) и любая из его вершин называются инцидентными. Принято говорить, что ребро (u, v) соединяет вершины u и v, а дуга (u, v) начинается в вершине u и кончается в вершине v.
Графический Изоморфные графы Два графа называются изоморфными, если существует перестановка вершин, при которой они совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между их вершинами и рёбрами, которое сохраняет смежность и инцидентность (графы отличаются только названиями своих вершин).
Остовной граф Остовом (неориентированного) связного графа G=(V,E) называется его частичный граф, являющийся деревом. Остовной граф – когда количество вершин остовного дерева соответствует количеству вершин исходного графа. · Построение остовного дерева: Выбираем произвольное ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. · Всего n -1ребро!!! Числом вершинной связности (или просто числом связности) χ(G) графа G называется наименьшее число вершин, удаление которых приводит граф G к несвязному или одновершинному графу. Числом реберной связности λ(G) графа G называется наименьшее число ребер, удаление которых приводит к несвязному графу.
Остовной граф Остовом (неориентированного) связного графа G=(V,E) называется его частичный граф, являющийся деревом. Остовной граф – когда количество вершин остовного дерева соответствует количеству вершин исходного графа. Построение остовного дерева: Выбираем произвольное ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. · Всего n -1ребро!!! Алгоритмы Краскала и Прима – алгоритмы построения минимального остовного дерева (поиск кратчайшего соединения). Алгоритм Краскала: Пусть есть связный граф, содержащий n вершин. Шаг1: ребра графа упорядочим в порядке их неубывания веса. Шаг2: начиная с 1го: самый маленький вес, добавляем новое ребро с условием: не должно приводить к циклу. Шаг3: повторяем Шаг2 пока число ребер в графе не станет равно n-1. Получившееся дерево является минимальным остовным деревом графа G. Алгоритм долгий, потому что должны выполнятся сортировки. При m ребрах это m*log2m операций. Алгоритм Прима: Шаг1: без упорядочивания выбираем произвольную вершину и ребро, соединяем ее с близкими по весу соседом. Шаг2: найти еще (не присоединенную) вершину, лежащую ближе всего к одному из присоединенных и соединить с ней. Шаг3: повторяем шаг2 пока все вершины не будут присоединены. n(n-1)/2 – количество решений, где n – количество вершин.
Begin for v Î V do D [ v ]:= A [ s, v ]; D [ s ]:= 0; for k:= 1 to n – 2 do for v Î V \ { s } do for u Î V do D [ v ]:=min(D [ v ], D [ u ] + A [ u, v ]) End Очевидно, что временная сложность алгоритма есть O(n 3). Мы можем, конечно, закончить вычисления, когда выполнение цикла 4 не вызывает изменения ни одной из переменных D [ v ], v Î V. Это может наступить для k < n – 2, однако такая модификация алгоритма не изменяет существенным образом его сложности. Для редких графов (m << n 2) удобнее представлять граф списками инцидентности ПРЕДШ [ v ], v Î V. Заменяя строку 5 на for u Î ПРЕДШ [ v ] do D [ v ]:=min(D [ v ], D [ u ] + A [ u, v ]), получаем алгоритм со сложностью O(nm).
Пути в бесконтурном графе Случай, для которого известен алгоритм нахождения расстояний от фиксированной вершины за время O(n 2) — случай, когда граф является бесконтурным (нет замкнуых путей)(веса дуг могут быть произвольными). Лемма. В произвольном бесконтурном графе вершины можно перенумеровать так, что каждая дуга будет иметь вид á vi, vj ñ, где i < j. Псевдокод На каждом шаге алгоритм генерирует двухмерную матрицу W, W[i,j]= for k = 1 to n for i = 1 to n for j = 1 to n W[i,j] = min(W[i,j], W[i,k] + W[k,j]) Если требуется найти сами пути, то перед началом работы алгоритма построим матрицу P с начальными значениями элементов pij=i. Каждый раз, когда на dik + dkj<dij, выполним присваивание pij:=pkj. В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение pij будет равно номеру предпоследней вершины в пути между i и j (либо pij=i, если путь не существует).
Теорема Галлаи альфа0 + бетта0 = n = альфа1 + бетта1
Плоский граф. Планарный граф. Укладка графа на плоскость. Грань в плоском представлении графа. Гомеоморфизм графов. Теорема Понтрягина-Куратовского. Будем говорить, что граф укладывается на поверхности S, если его можно так нарисовать на S, что никакие два его ребра не пересекаются. Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф называют планарным, если его можно уложить на плоскости; плоский граф — это граф, уже уложенный на плоскости.
Плоские графы — это простые циклы, деревья. Гранью в плоском представлении графа G называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов. Простой цикл, ограничивающий грань, называется границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро. Два графа гомеоморфны (или тождественны с точностью до вершин степени 2), если они оба м б получены из одного и того же графа «включением» в его ребра новых вершин степени 2 Теорема Эйлера Для всякого плоского представления связного плоского графа без перегородок число вершин (V), число ребер (E) и число граней с учетом бесконечной (R) связаны соотношением V – E + R = 2 Триангуляция графа. Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Каждая грань в плоском представлении максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф называют триангулированным. Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
Множества. Отношение принадлежности. Универсум и пустое множество. Мощность множества. Отношение включения. Подмножество, надмножество, собственное подмножество. Булеан множества. Парадокс Рассела «Произвольная совокупность определенных предметов нашей интуиции или интеллекта, которые можно отличить один от другого и которые представляются как единое целое, называется множеством. Предметы, которые входят в состав множества, называются его элементами» · Через Î обозначается отношение принадлежности, т.е. x Î A означает, что элемент x принадлежит множеству A. · Если x не является элементом множества A, то это записывается x Ï A или x A. · Два множества A и B считаются равными, если они состоят из одних и тех же элементов. Пишется A = B, если A и B равны, и A ¹ B в противном случае. · Через Í обозначается отношение включения множеств, т.е. A Í B означает, что каждый элемент множества A является элементом множества B. В этом случае A называется подмножеством B, а B — надмножеством A. Если A Í B и A ¹ B, то A называется собственным подмножеством B, и в этом случае пишем A Ì B. · Мощностью (или кардинальным числом) множества называется количество элементов в нем. · Множества могут быть конечными (т.е. состоящими из конечного числа элементов) и бесконечными. · Множество мощности 0, не содержащее элементов, называется пустым и обозначается Æ. · Некоторое, общее для всех множеств данной мощности, надмножество, называется универсальным множеством или универсумом и обозначается обычно как U. · Фиксируем множество Ω. Мы рассматриваем подмножества Ω, т.е. множества, содержащиеся в Ω. Семейство всех подмножеств Ω обозначаем через P(Ω); P(Ω) — множество, все элементы которого сами являются множествами. Термин семейство понимается здесь в следующем смысле: семейство — множество, все элементы которого сами являются множествами (вместо множества множеств говорим семейство множеств).
Теорема. Если мощность конечного множества А равна 2. Способы задания множеств. Парадокс Рассела. · Перечислением элементов; · Описание характеристических свойств или характеристическим предикатом; · Порождающей процедурой (например, индуктивными или рекурсивными правилами). а) б) в) Парадокс Рассела. Рассмотрим все множества, не содержащие самих себя. Рассмотрим множество всех таких множеств. Тогда: если оно не содержит себя, то оно содержит себя.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.199.188 (0.082 с.) |
 ;
;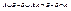 ;
; ;
;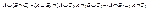 ;
;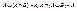 ;
;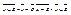 ;
;
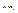 ) – результат операции i элемента на j -ый. Группоид, обозначаемый символом (A, ©) — множество A, на котором задана некоторая бинарная операция, обозначаемая ©. Если множество группоида конечно, ½A½ = n, то таблица операции группоида есть таблица n ´ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Группоид можно считать заданным, если выписана его таблица операции.
) – результат операции i элемента на j -ый. Группоид, обозначаемый символом (A, ©) — множество A, на котором задана некоторая бинарная операция, обозначаемая ©. Если множество группоида конечно, ½A½ = n, то таблица операции группоида есть таблица n ´ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Группоид можно считать заданным, если выписана его таблица операции.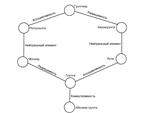
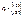 ,
, 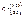 ,
, 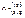 ,
, 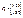 ,
, 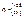
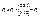 ,
, 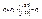 ,
, 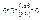 ,
, 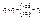 ,
, 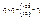
 . Матрица W содержит длины кратчайших путей между всеми вершинами графа. Перед работой алгоритма матрица W заполняется длинами рёбер графа.
. Матрица W содержит длины кратчайших путей между всеми вершинами графа. Перед работой алгоритма матрица W заполняется длинами рёбер графа. , то число всех подмножеств А равно
, то число всех подмножеств А равно 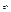 , то есть
, то есть 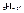 . Множество всех подмножеств множества М называется булеаном и обозначается
. Множество всех подмножеств множества М называется булеаном и обозначается  . Для конечных множеств выполняется:
. Для конечных множеств выполняется: 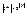 .
.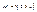 .
.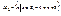 .
.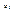
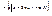 .
.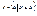 . Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если
. Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если 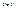 , то
, то 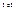 . С другой стороны, если
. С другой стороны, если  не является множеством.
не является множеством.