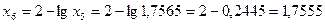Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
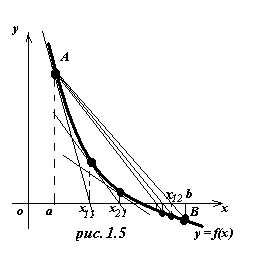
Комбинированное применение методов хорд и касательных.
Воспользуемся способами хорд и касательных:
Величины х11 и х12 принадлежат промежутку изоляции, причем Построим новую пару приближений к корню:
Точки х21 и х22 на числовой оси между точками х11 и х12, причем и т. д. Каждая из последовательностей: х11, х21, х31 ............. х12, х22, х32 ............. стремится к искомому корню, причем одна из последовательностей монотонно возрастает, а другая монотонно убывает. Пример 1.4: Комбинируя способы хорд и касательных найти приближенное значение корня уравнения х3 + х2 -11 = 0, изолированного в промежутке (1; 2) с точностью до 0,001. Решение. Имеем f(x) = х3 + х2 -11,
Искомый корень принадлежит промежутку (1,9; 1,94). f(1,9)= -0,531, f(1,94) =0,065, Следовательно,
Так как значения х21 и х22 , вычисленные с точностью до 0,001, совпали, то приближенным значением корня будет 1,936. Метод итераций. Если каким нибудь способом получено приближенное значение х0 корня уравнения, то уточнение приближения можно осуществить методом итераций (методом последовательных приближений). Пусть задано уравнение f(x) = 0, представим его в виде Пределом последовательности х1, х2, х3,..... хп .... является единственный корень уравнения f(x) = 0 на отрезке [a; b]. Пример 1.5: Способом итераций найти приближенное значение корня уравнения 2 – lgx – x = 0 с точностью до 0.001 Решение. Найдем интервал изоляции действительного корня уравнения. Представим уравнение в виде: lgx = – x + 2 Построим графики функций у = lgx и у = – x + 2. Точка М пересечения графиков имеет абсциссу в промежутке [1; 2]. Пусть х0 = 1. Запишем исходное уравнение в виде х = 2 – lgx.
Найдем приближения:
Таким образом, искомый корень с точностью до 0,001 равен 1,755 Упражнения. Отделить корни уравнения графически и методом исследования отрезков.
Решить способом хорд и касательных с точностью до 0,01 следующие уравнения:
Применив комбинированный способ хорд и касательных решить уравнение.
Решить способом итераций с точностью до 0,01 следующие уравнения.
ГЛАВА II. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 879; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.240.61 (0.01 с.) |
 Пусть требуется вычислить действительный корень уравнения f(x) = 0, изолированный на отрезке [a; b]. Предполагается, что f (a) и f(b) имеют разные знаки (т.е. f (a)* f(b) < 0), а каждая из производных сохраняет определенный знак на отрезке изоляции. Возьмем на отрезке [a; b] такую точку х0, что
Пусть требуется вычислить действительный корень уравнения f(x) = 0, изолированный на отрезке [a; b]. Предполагается, что f (a) и f(b) имеют разные знаки (т.е. f (a)* f(b) < 0), а каждая из производных сохраняет определенный знак на отрезке изоляции. Возьмем на отрезке [a; b] такую точку х0, что 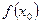 имеет тот же знак что и
имеет тот же знак что и  , т.е. выполняется условие:
, т.е. выполняется условие: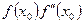 >0.
>0.

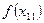 и
и 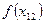 имеют разные знаки.
имеют разные знаки.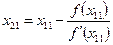
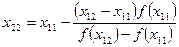
 и
и 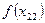 имеют разные знаки.
имеют разные знаки. =3х2+2х
=3х2+2х  = 6х+2. В указанном промежутке
= 6х+2. В указанном промежутке 




 , где
, где  <1 всюду на отрезке [a; b], содержащем единственный корень
<1 всюду на отрезке [a; b], содержащем единственный корень  . Исходя из некоторого начального значения
. Исходя из некоторого начального значения  можно построить последовательность:
можно построить последовательность:  ,
,  ,
,  .......
.......  ...
... = 2 – lgx,
= 2 – lgx, 

 в промежутке [1; 2], следовательно, способ итераций применим.
в промежутке [1; 2], следовательно, способ итераций применим.