Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сокращение и «расширение» дроби
Величина дроби не изменится, если числитель и знаменатель дроби умножить на одно и то же число. Например:
Такое преобразование дроби называется «расширением» дроби. Дробь Величина дроби не изменится, если числитель и знаменатель дроби разделить на одно и тоже число. Например: Такое преобразование называется сокращением дроби. Проценты Слово «процент» происходит от латинского «procento», что означает «с сотни». Процент — это сотая часть числа, обозначается знаком %. Всякое целое число (например 1) составляет 100%. Его сотая часть 1: 100 = 0,01. Следовательно, 1% от единицы составит 0,01. Если в задаче величина в целом неизвестна, а известны только ее части, то она принимается за 100% или за 1 (единицу). Когда целое состоит из каких — то частей, то эти части составляют дроби, сумма которых равна целому (1). Пропорционально этим дробям часть целого можно взять и в процентах. Если весь объем — 100%, то каждая часть (каждая дробь) составляет величину больше 0%, но меньше 100%, а сумма всех частей в процентах равна 100%. Процент какой — то величины — это часть (доля) этой же величины, поэтому, если 1 = 100%, то и каждая дробь (обыкновенная или десятичная) равна какому — то проценту от 1. 5% = 0,05 = 10% = 0,1 = 20% = 0,2 = 25% = 0,25 = 40% = 0,4 = 50% = 0,5 = 75% = 0,75 = 80% = 0,8 = Округление чисел Пример: округлите до тысячных число 0,3442524. Тысячные – это третий разряд после запятой, значит, нам надо смотреть на четвертый цифру: 0,344 2 524 – в данном случае это 2, поэтому округляем в меньшую сторону и получаем 0,344. Напомним, что при цифрах 0,1,2,3,4 округляем в меньшую сторону. При цифрах 5,6,7,8,9 округляем в большую сторону. Таким образом у нас есть пять случаем и в округлении в меньшую и большую сторону.
Определение Текстовые задачи ― это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами. Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
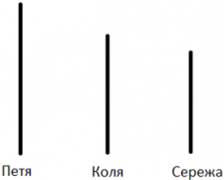
Пример: Коля наклеил на 5 листов по 2 наклейки. Сколько наклеек наклеил Коля? Условие: Коля наклеил на 5 листов по 2 наклейки. Вопрос: Сколько наклеек наклеил Коля? Решение любой текстовой задачи можно разделить на несколько основных этапов: · Работа с условием; · Составление уравнения; · Проверка ответа; · Для одного уравнения может быть составлено множество различных условий. Пример: Уравнение: 2 + х = 5. Условие 1: Маша и Петя вместе нашли 5 грибов. Маша нашла 2. Сколько грибов нашел Петя? Условие 2: Букет состоит из ромашек и колокольчиков. Всего в букете 5 цветков, из них 2 ромашки. Сколько колокольчиков в букете? Условие 3: На елке было 5 игрушек. Две из них упали и разбились. Сколько игрушек осталось на елке? Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица. Пример: Петя выше Коли, Сережа ниже Коли. Кто выше? Иллюстрация:
Из рисунка сразу понятен ответ: Петя выше всех. Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Алгебраическая зависимость Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д. При составлении уравнения особое значение играют используемые предлоги: «в» и «на». Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи? Решение: Пусть П ― рост Пети, К ― рост Коли, С ― рост Сережи. Кстати, обратите внимание на этот приём ― выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением. Выразим рост мальчиков. Петя выше Коли на 20 см: П – 20 = К. Сережа ниже Коли на 10 см: К = С + 10. Подставим в первое уравнение рост Коли: П – 20 = С + 10. Нам нужно найти, на сколько см Петя выше Сережи: П – С. П – 20 = С + 10; П – С = 20 + 10; П – С = 30. Получаем, что Петя выше Сережи на 30 см. Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение: Пусть М ― количество снежинок, которое сделала Маша, К – снежинки Коли, Р ― снежинки Ромы. Маша сделала в два раза больше снежинок, чем Коля: К = М/2. Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4. Вместе ребята сделали 12 снежинок: М + К + Р = 12. Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12. М = 4. Маша сделала 4 снежинки.
Процентная зависимость Процент ― это всегда доля какого-то числа. 100% ― все число; 50% ― половина; 25% ― четверть. Чтобы найти 1%, необходимо поделить всё число на 100. Пример: Есть 100 яблок. 1% от всех яблок ― Есть 200 груш. 1% от всех груш ― Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом ― соответствующие проценты. Пример: 200 груш ― 100 %; 2 груши ― 1 %. Прогрессия отражает зависимость величин. По-другому это можно записать в виде двух дробей: Исходя из правил работы с дробями, получаем правила работы с пропорцией: · Внутри одной дроби можно сокращать значения. · Произведение накрест лежащих значений равно: 200 ∙ 1 = 2 ∙ 100. Эту тему мы еще подробно пройдем на курсе. Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу ― обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.
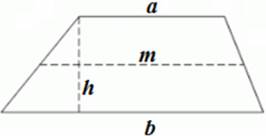
Трапеция Трапеция ― это четырёхугольник, у которого две противоположные стороны параллельны. Элементы трапеции:
a и b ― основания трапеции, a || b; h ― высота трапеции (расстояние между основаниями); m ― средняя линия трапеции (отрезок, соединяющий середины боковых сторон трапеции). Средняя линия трапеции равна полусумме оснований: m = m || a и m || b. Виды трапеций: 1) Прямоугольная ― трапеция, имеющая прямые углы при боковой стороне: · боковая сторона является высотой.
2) Равнобедренная ― трапеция, у которой боковые стороны равны: · углы при основаниях равны · длины диагоналей равны
Свойства трапеции: · Сумма внутренних углов трапеции (как и любого четырехугольника) равна 360°. · Сумма углов, прилежащих к боковой стороне, равна 180°. · В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон. · Если трапецию можно вписать в окружность, то трапеция ― равнобедренная. · Около равнобедренной трапеции можно описать окружность. Площадь трапеции: S = S = m ∙ h, где m ― средняя линия трапеции.
Треугольники
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 798; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.237 (0.024 с.) |
 =
= 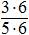 =
=  ;
;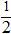 =
= 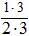 =
=  ;
;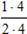 =
=  ;
;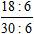 =
=  ;
;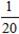 ;
;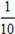 ;
; ;
; ;
; ;
; ;
;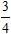 ;
; .
.
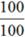 = 1 яблоко.
= 1 яблоко.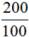 = 2 груши.
= 2 груши.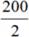 =
= 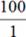 .
.
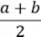 и параллельна им:
и параллельна им:

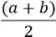 ∙ h;
∙ h;