Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое занятие № 3. Алгебра логики. Операции над высказываниями
Цель занятия Цель занятия: ознакомиться с понятием «высказывание». Знать основные логические операции. Уметь выполнять операции над высказываниями, читать и строить таблицу истинности. Теоретический материал для практического занятия №3 Логика – одна из древнейших наук. Её основателем считается древнегреческий мыслитель Аристотель (384 – 322гг. до н. э.), который первым систематизировал формы и правила мышления, обстоятельно исследовал категории: понятие и суждение, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Продолжение развития логики связано с математической логикой. Основоположником математической логики считается великий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). Он попытался построить первые логические исчисления: арифметические и буквенно-алгебраические. Но Лейбниц высказал только идею, а развил её окончательно англичанин Джордж Буль (1815-1864). Он вывел для логических построений особую алгебру (алгебру логики). В отличие от обычной логики, в ней символами обозначаются не числа, а высказывания. Алгебра логики (булева алгебра) изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е годы 19 в.) и дальнейшим развитием математической логики (последняя четверть 19 в. и первая половина 20 в.) предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания. Высказыванием в математике называют предложение, относительного которого имеет смысл вопрос истинности или ложности его. В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого слова: «и, или, если…, то», которые называют логическими связками. Предложения, образованные из других предложений с помощью логических связок, называют составными. Выделяют пять основных логических связок, которые позволяют получить новые высказывания: 1) Отрицание – это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание обозначается`
2) Конъюнкция высказываний А и В – это высказывание АÙB, которое истинно, когда оба высказывания истинны, и высказывание АÙB ложно, когда хотя бы одно из этих высказываний ложно. Конъюнкция получается из двух данных высказываний А и В с помощью союза «и». Пример 1. Высказывание А= «студент сдаёт сессию без троек, двоек». Высказывание В= «студент получает стипендию». Конъюнкцией высказываний А и В будет высказывание АÙB=«студент сдаёт сессию без троек, двоек и студент получает стипендию». 3) Дизъюнкция высказываний А или В – это высказывание АÚ B, которое истинно, когда истинно хотя бы одно из этих высказываний, и высказывание АÚ B ложно, когда оба высказывания ложны. Дизъюнкция получается из двух данных высказываний А, В с помощью союза «или». Пример 2. Для высказываний А и В примера 1 дизъюнкция имеет вид: АÚB=«студент сдаёт сессию без троек, двоек или студент получает стипендию или то и другое». 4) Импликация образуется из двух данных высказываний А и В с помощью слов «если…, то…». Импликация обозначается: АÞВ (если А, то В). Пример 3. Для высказываний А и В примера 1 импликация имеет вид: АÞВ = «если студент сдаёт сессию без троек, двоек, то студент получает стипендию». 5) Эквиваленция образуется из двух данных высказываний А и В с помощью слов «тогда и только тогда, когда…». Эквиваленция обозначается А Û В. Пример 4. Для высказываний А и В примера 1 эквиваленция имеет вид: А ÛВ= «студент сдаёт сессию без троек, двоек тогда и только тогда, когда студент получает стипендию». Пример 5. Эквиваленция из высказываний В и А примера 4 будет: ВÛА = «студент получает стипендию тогда и только тогда, когда студент сдаёт сессию без троек, двоек». В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывания можно представить некоторой переменной величиной, значением которой может быть только «0» или «1». Если высказывание истинно, то его значение равно «1», если ложно, то равно «0».
Логические операции Истинность новых высказываний определяются только истинностью входящих в них высказываний. Построение из данных высказываний (или из данного высказывания) нового высказывания называется логической операцией. Знаки логических операций называются логическими связками. Логические связки могут быть: одноместными (унарными), двухместными (бинарными), трёхместными (тернарными) и т.д. В таблице 3.1 приведены основные логические операции (связки).
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.35.77 (0.008 с.) |
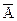 . Высказывание А=«студент сдал сессию». Высказывание
. Высказывание А=«студент сдал сессию». Высказывание