
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дальневосточный государственныйСодержание книги
Поиск на нашем сайте
Министерство здравоохранения Российской Федерации Дальневосточный государственный медицинский университет Кафедра социальной медицины, Экономики и организации здравоохранения
Относительные величины в медицинской статистике (методические рекомендации для студентов) Хабаровск - 1999 Цель данных методических рекомендаций - научить правильно применять абсолютные и относительные величины в медицинской практике. Освоить методику преобразования абсолютных величин в относительные показатели, оценку их достоверности. Знать методику построения и уметь анализировать динамические ряды. После изучения данной темы студент должен: Знать: 1. виды относительных показателей 2. методы оценки достоверности относительного показателя 3. методы оценки достоверности разности относительных показателей показатели динамического ряда 4. показатели динамического ряда 5. виды графических изображений, применяемых в медицинской статистике Уметь: 1. рассчитывать и оценивать относительные показатели 2. определять достоверность относительных величин 3. определять достоверность разности относительных показателей оценивать показатели динамического ряда 4. рассчитывать и оценивать показатели динамического ряда 5. изображать относительные величины и показатели динамического ряда графически.
Относительные величины в медицинской статистике.
При проведении любых статистических исследований в конечном итоге получаются абсолютные величины. Абсолютная величина - это результат подсчета общего числа единиц изучаемой совокупности в целом или по отдельным его группам. Например, при подсчете числа врачей в нашей стране можно получить общую суммарную численность врачей и численность отдельных групп врачей в зависимости от их специальности. Получение и практическое использование абсолютных величин является основой статистики, но сами по себе они имеют довольно ограниченное познавательное значение. Характеризуя абсолютные размеры изучаемого явления и составляющих его частей, абсолютные величины не могут быть применены при сравнении аналогичных явлений между собой или при оценке изменения какого-либо одного явления во времени. Поясним это на таком примере: за год в районе А. родилось 3800 человек, а в районе Б. - 2500 человек. Можно ли сделать вывод о том, в каком из районов рождаемость выше? Конечно, нет, так как для характеристики такого явления как рождаемость, необходимо знать численность населения данных районов (т.е. еще одну абсолютную величину). Поэтому для сравнения - главной цели статистического анализа - применяется производные величины. Одной из разновидностей производных величин являются относительные величины, в практике часто называемые коэффициентами или относительными показателями (Р). Относительная величина получается в результате деления одной абсолютной величины (а) на другую (в):
Вернемся к нашему примеру. Зная численность населения каждого из районов, мы можем рассчитать относительные показатели - показатели рождаемости в районе А. и районе Б. Среднегодовая численность населения района А. составила 250000 человек, а района Б. - 130000 человек. Следовательно, показатель рождаемости (число родившихся живыми за год на 1000 населения) в районе А. составит: 3800 х 1000 Р А = ---------------------- = 15,2 ‰ в районе Б: 2500 х 1000 Р Б = ---------------------- = 19,2 ‰ Если бы мы для оценки рождаемости сопоставляли между собой абсолютные величины, то сделали бы ошибочный вывод, так как абсолютное число рождений в районе А. выше. В действительности же, проведя расчет рождений на каждую тысячу населения получаем обратный вывод: рождаемость выше в районе Б.
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН.
Величина результатов, получаемых при любых вычислениях всегда отклоняется от их математической вероятности в силу недостаточно большого числа проводимых наблюдений, поскольку абсолютно достоверный результат может быть получен лишь при бесконечно большом числе наблюдений. Другими словами, результаты вычислений всегда имеют свою ошибку и чем больше число наблюдений, тем точнее результат вычислений, меньше размер ошибки. Одной из особенностей биологических и медицинских исследований является относительно небольшое число наблюдений. Нередки случаи единичных наблюдений, результаты которых также должны подвергаться статистической обработке. Существует три основных метода определения достоверности относительных величин: вычисление ошибки относительной величины, определение достоверности разности двух относительных величин и метод доверительных интервалов. 1. Вычисление ошибки относительной величины. Ошибка относительной величины обозначается знаком (m) и рассчитывается по следующей формуле:
m =
где Р - относительная величина, q - альтернатива (величина, противоположная по значению Р) q = 1 - Р Если показатель выражен в процентах, то q = 100 - Р, если в промилле - то q = 1000 - Р и т.д. n - число наблюдений.
Данная формула используется для определения ошибки относительного показателя при числе наблюдений n>30 (большая выборка). Если же мы имеем дело с малой выборкой (n<30), ошибка относительного показателя должна рассчитываться следующим образом:
m =
Произведем расчет ошибки для какого-либо относительного показателя: В районе А. с населением 10000 жителей зарегистрировано 500 случаев заболевания гриппом. Интенсивный показатель заболеваемости населения гриппом будет равен:
500 х 1000 Р = -------------------- = 50 ‰
(50 случаев заболевания на каждую 1000 населения), следовательно, q = 1000 - 50 = 950 Ошибка этого показателя равна: m = Ошибка относительного показателя всегда имеет знак (±) и наименование, соответственно тому показателю, для которого она рассчитывается. Существует следующее правило: ошибка показателя должна быть в три раза меньше величины самого показателя. Т.е., например, если мы имеем относительный показатель, равный 2,0%, а его ошибка равна ± 0,8%, то такому показателю нельзя доверять, т.к. 0,8 х 3 = 2,4 и 2,0 < 2,4. В нашем примере ошибка в 3 раза меньше полученного показателя, следовательно, ему можно доверять. Достоверность относительного показателя с помощью ошибки определяется путем расчета доверительного интервала по следующей формуле: P = Pв ± t где: t - доверительный коэффициент, который может принимать значения 1, 2, 3. Pв - показатель выборочной совокупности. Если доверительный коэффициент равен 1, т.е. интервал P = Pв ± m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,68 (68%). Если доверительный коэффициент равен 2, т.е. интервал P = Pв ± 2m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,95 (95%). Если доверительный коэффициент равен 3, т.е. интервал P = Pв ± 3m, то вероятность того, что при повторных исследованиях показатель не выйдет за пределы данного интервала составляет 0,997 (99,7%). Какие из этих интервалов можно назвать доверительными? Из теории вероятностей известно, что вероятность, которой можно доверять, или доверительная вероятность, равная 0,95, считается достаточной для суждения о достоверности полученных результатов опыта. Вероятность, равная 0,997 считается еще более надежным критерием достоверности. Следовательно, интервалы колеблемости показателя P = Pв ± 2m и P = Pв ± 3m являются доверительными интервалами показателя. Произведем расчеты интервалов колеблемости показателя в нашем примере: Р = 50 ‰, m = ± 2,2 ‰
P ± m = 50 ± 2,2 = 47,8 - 52,2 P ± 2m = 50 ± 2 P ± 3m = 50 ± 3
Таким образом, мы можем утверждать, что показатель заболеваемости населения гриппом в районе А. фактически может приобретать любые значения в интервале 45,6 - 54,4 ‰ с достоверностью 0,95, и в интервале 43,4 - 56,6 ‰ с достоверностью 0,997. То есть, если при повторных изучениях заболеваемости населения гриппом мы будем получать значения, входящие в эти интервалы, все они будут достоверными. Таким образом, при анализе любого статистического материала, рассчитав какой-либо относительный показатель, нельзя сразу делать заключение о величине исследуемого явления. Необходимо, рассчитав ошибку этого показателя, обязательно рассчитать один из доверительных интервалов (как минимум P ± 2m) и только тогда делать заключение о величине исследуемого явления. Так, в нашем примере мы не можем утверждать, что показатель заболеваемости населения гриппом в районе А. составил 50 ‰, мы должны сделать заключение, что он с вероятностью 0,95 колеблется в пределах от 45,6 ‰ до 54,4 ‰ и любое значение этого же показателя в этом интервале, полученное при повторных исследованиях, будет достоверно. Особый интерес представляет методика расчета ошибки относительного показателя при его значениях, равных 0% и 100%. Действительно, при расчете ошибки показателя по уже представленной форме получаем: а) Р = 0%; n = 125; m = б) Р = 100%; n = 125; m =
В таких случаях можно сделать ошибочный вывод о том, что у относительной величины нет ошибки, т.е. она абсолютно достоверна. Однако это противоречит закону больших чисел, поскольку эти результаты могут быть получены и на малом числе наблюдений и даже на единичных наблюдениях, следовательно, они обязательно должны отклоняться от математически достоверных величин, т.е. иметь ошибку. Для таких случаев предложена другая методика расчета ошибки относительной величины: m = где t - доверительный коэффициент n - число наблюдений. Приведем пример расчета ошибки относительного показателя, имеющего величину 100%. В терапевтическом отделении для лечения 100 больных применили новое лекарственное средство, оказавшееся эффективным во всех случаях, т.е. в 100%. Возникает вопрос: действительно ли эффективен этот препарат во всех случаях? Для того, чтобы ответить на этот вопрос, необходимо рассчитать ошибку полученного показателя: Р = 100 %; n = 100
m =
Это означает, что при дальнейшем увеличении числа наблюдений в 95% случаев (т.к. t = 2) препарат будет неэффективен у 3,8% лечившихся больных. При применении данной формулы ошибка не имеет знака (±), т.к. отклонение показателя может быть только в одну сторону - при 0% в большую, при 100% в меньшую. Кроме того, при определении доверительного интервала нет необходимости удваивать или утраивать ошибку, т.к. введя в формулу величину t мы сразу задаем необходимую его точность.
Величин.
Для расчета достоверности разности двух относительных показателей используется специальная формула, предложенная английским ученым Стьюдентом:
где Р1 и Р2 - сравниваемые относительные показатели m1 и m2 - ошибки сравниваемых показателей t - критерий достоверности. Величина критерия всегда получается и оценивается в абсолютных числах и без учета знака, получившегося при расчете величины разности Р1 и Р2. Оценка результата, полученного при вычислении критерия достоверности, в значительной степени зависит от числа наблюдений (n) в ходе исследования. Для того, чтобы признать разность относительных величин достоверной, необходимо иметь следующие значения критерия: а) при n > 100 t б) при 30 < n < 100 t в) при n < 30 t определяется по специальным таблицам Стьюдента-Фишера. Таблица значений критерия t (Стьюдента)
Рассмотрим методику расчета достоверности разности двух относительных величин на следующем примере: В районе А. с населением 10000 человек показатель заболеваемости гриппом составил 50 ‰ (Р1), в районе В. с таким же населением этот показатель был равен 30 ‰ (Р2). Нам необходимо выяснить, действительно ли заболеваемость гриппом выше в районе А., чем в районе В., или же эта разность несущественна.
Р1 = 50 ‰; n1 = 10000; m1 =
Р2 = 30 ‰; n2 = 10000; m2 =
t =
Число наблюдений в нашем примере 10000 (больше 100), величина критерия Стьюдента 7,2 (больше 2,6), следовательно, мы с большой достоверностью можем утверждать, что различие сравниваемых показателей существенно, т.е. в районе А. заболеваемость гриппом действительно выше, чем в районе В. Рассмотрим еще один пример: При анализе годового отчета главный врач участковой больницы обнаружил, что в 1995 году доля заболевших ангинами составила 2,5% от общего числа заболевших, а в 1996 году доля таких больных была 4,0%. Достоверно ли увеличение доли заболевших ангиной? Ответ на этот вопрос можно дать, рассчитав достоверность разности этих показателей: При различных числах наблюдений в сравниваемых группах оценка критерия Стьюдента должна производиться по требованиям для группы с меньшим числом наблюдений. Следовательно, чтобы разность показателей в нашем примере была достоверной, величина критерия t должна быть равна или больше 3, т.к. число наблюдений в опыте (n1 = 95) меньше 100, но больше 30. Полученный результат значительно меньше требуемой величины критерия t, следовательно, действительного увеличения удельного веса заболевших ангиной не произошло.
Министерство здравоохранения Российской Федерации Дальневосточный государственный медицинский университет
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.52.43 (0.01 с.) |


 Так как в результате деления одного целого числа на другое как правило получается дробное число, то его принято умножать на 100, 1000, 10000, соответственно полученный результат будет измеряться в процентах (%), промилле (‰), продецимилле (‰).
Так как в результате деления одного целого числа на другое как правило получается дробное число, то его принято умножать на 100, 1000, 10000, соответственно полученный результат будет измеряться в процентах (%), промилле (‰), продецимилле (‰).

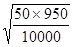 = ± 2,2 ‰
= ± 2,2 ‰ m
m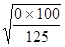 = 0
= 0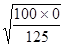

 = 3,8 %
= 3,8 % = t
= t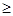 2,6
2,6 =
=  =
=  = ± 1,7 ‰
= ± 1,7 ‰ = 7,2
= 7,2


