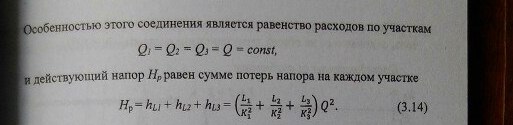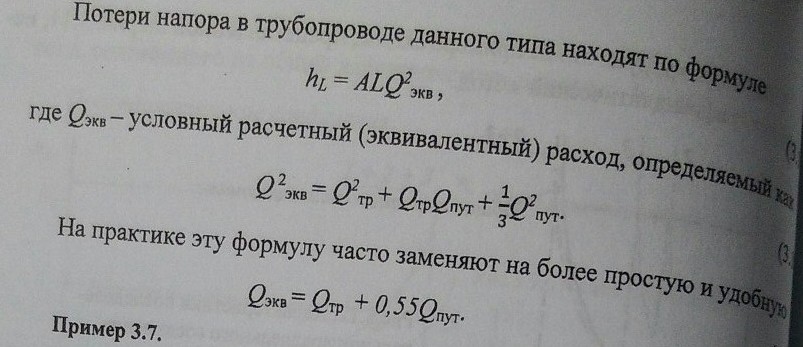Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теории подобия потоков, критерии подобия: Ньютона, Рейнольдса, Эйлера и Фруда ⇐ ПредыдущаяСтр 2 из 2
Теория подобия — метод математического моделирования, основанный на переходе от обычных физических величин, влияющих на моделируемую систему, к обобщённым величинам комплексного типа, составленным из исходных физических величин, но в определённых сочетаниях, зависящих от конкретной природы исследуемого процесса. Комплексный характер этих величин имеет глубокий физический смысл отражения взаимодействия различных влияний. Теория подобия изучает методы построения и применения этих переменных и применяется в тех случаях математического моделирования, когда аналитическое решение математических задач моделирования невозможно из-за сложности и требований к точности. Число Рейнольдса есть мера отношения сил инерции, действующих в потоке, к силам вязкости. Плотность в числителе выражения Число́ Фру́да, или критерий Фруда, — один из критериев подобия движения жидкостей и газов, является безразмерной величиной. Применяется в случаях, когда существенно воздействие внешних сил. Число Фруда характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа: Число Эйлера {Eu} — безразмерный коэффициент, имеющий место в уравнениях Навье — Стокса, описывающий отношение между силами давления на единичный объём жидкости (или газа) и инерционными силами.
где Число Ньютона (Ne или Nt) — критерий подобия в механике, выражающий отношение работы внешних сил к кинетической энергии тела. Этот критерий также известен как силовое число, или число мощности.
Число Ньютона можно определить двумя способами. Для твёрдого тела: Для сплошной среды: , где m — масса тела; p — его плотность; F — внешняя сила; L — характеристическая длина; v — скорость.
Гидравлическое моделирование. Основное правило моделирования и его применение при частичном подобии потоков Моделирование изучает натур. Объектов явлений с помощью функций. Моделирование применяется, когда нет объекта или когда объект недоступен (база для моделирования) Основное правило
1) Физическое 2) Аналоговая природные явления и природа разные 3) Математическая представляет из себя программу расчета Гидравлическое моделирование осуществляется на специальных стендах, включающих фрагменты основных рабочих элементов аппарата в натуральную величину. В качестве рабочих сред используют модельные системы воду, воздух, песок и т. п. При гидравлическом моделировании выявляют закономерности, определяющие гидравлическое сопротивление и производительность аппарата для различных типов контактных устройств.
Истечение жидкостей из отверстий и насадков. Коэффициенты истечения, расчет скоростей и расходов. Дальность вылета струи.
16) Расчеты простых трубопроводов: основные задачи и методы расчета
17) Гидравлический удар в трубах, расчет ударного давления
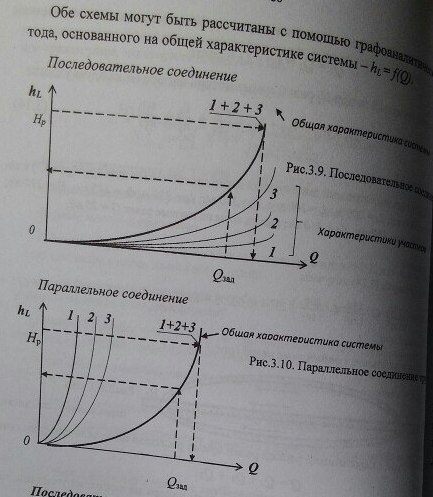
18) Расчеты сложных трубопроводных систем: последовательного, параллельного и разветвленного типов. Гидравлическая характеристика системы.
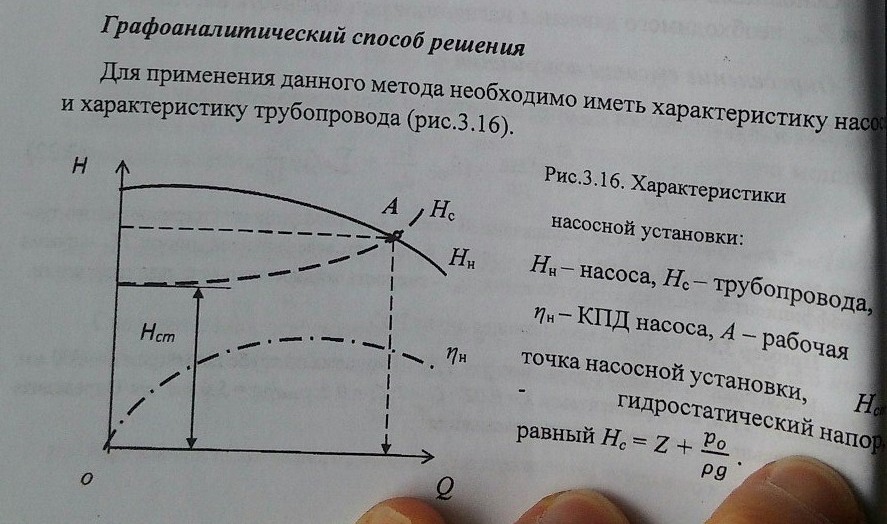
19 и 20) Расчеты простых насосных трубопроводов и расчеты сложных насосных систем
|
|||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.009 с.) |
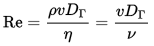 характеризует инерцию частиц, отклонившихся от движения по прямой, а вязкость в знаменателе показывает склонность жидкости препятствовать такому отклонению. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине (ввиду внутреннего трения). Если у потока число Рейнольдса достаточно большое (выше критической величины), то жидкость можно рассматривать как идеальную. В таком случае вязкостью можно пренебречь.
характеризует инерцию частиц, отклонившихся от движения по прямой, а вязкость в знаменателе показывает склонность жидкости препятствовать такому отклонению. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине (ввиду внутреннего трения). Если у потока число Рейнольдса достаточно большое (выше критической величины), то жидкость можно рассматривать как идеальную. В таком случае вязкостью можно пренебречь. где v — характерный масштаб скорости, g — ускорение, характеризующее действие внешней силы, L — характерный размер области, в которой рассматривается течение.
где v — характерный масштаб скорости, g — ускорение, характеризующее действие внешней силы, L — характерный размер области, в которой рассматривается течение.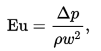
 плотность,
плотность, 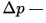 перепад давления, расходуемый на преодоление гидравлического сопротивления, w — скорость.
перепад давления, расходуемый на преодоление гидравлического сопротивления, w — скорость.
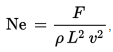
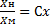 значит моделирование возможно
значит моделирование возможно