
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функціональні та степеневі ряди .Інтервал та радіус збіжності степеневого ряду ⇐ ПредыдущаяСтр 2 из 2
Ряд а+ а a Степеневим рядом за степенями двочлена х — хо, де x а Для кожного степеневого ряду існує таке дійсне додатне число R, що при x ˂ R ряд (15) збігається, а при x ˃ R розбігається. Проміжок (- R; R) називається інтервалом збіжності, а число R радіусом Збіжності ряду 21. Ряди Тейлора та Маклорена. Тригонометричний ряд Фур’є Нехай функція Тригонометричним рядом Фур'є називають функційний ряд виду
Частинну (часткова) похідну від функції f (x, y) за аргументом y визначають аналогічно.
23. Скалярне поле. Похідна за напрямом. Градієнт Скалярним полем - називають називають частину простору(увесь простір), у кожній точці якого відповідно до певного закону задано числове значення деякої скалярної величини. Похідна за напрямком - це узагальнення поняття похідної на випадок функції кількох змінних. Похідна за напрямом показує, наскільки швидко функція змінюється при русі вздовж заданого напряму. Градієнт — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Локальний екстремум. Функції багатьох змінних Диференціальні рівняння, основні означення.Рівняння з відокремлюваними змінними,однорідні, в повних диференціалах. Лінійні диференціальні рівняння першого та другого порядку.Рівняння вищих порядків.
Диференціальне рівняння — це рівняння, в якому невідомою величиною диференціал Рівняння вигляду P (x) dx + Q (y) dy =0. називається рівнянням з відокремленими змінними. Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду 26 Основні поняття комбінаторики. Правила комбінаторики Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність того, що вона відбудеться при заданих умовах. Ймові́рність — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. 27. Ймовірність події. Класифікація подій. Операції над подіями Ймові́рність — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню. Подія — результат випробування. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається літерою U. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається літерою V. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. 28. Послідовність незалежних випробувань.Формули Бернуллі, Пуассона У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів. Якщо ймовірність Р настання події А в кожному з випробувань стала, то ймовірність
Формула Пуассона Якщо ймовірність p настання події А в кожному випробуванні постійна, близька до нуля, а число незалежних випробувань n досить велике, то імовірність Pn (k) того, що в n незалежних випробуваннях подія А наступить k разів, наближено дорівнює:
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.218.62 (0.03 с.) |
 де членами ряду
де членами ряду 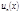 є функції від аргументу х, називається функціональним рядом. При х=х0 ряд перетворюється на числовий. Степеневим рядом, називається функціональний ряд вигляду
є функції від аргументу х, називається функціональним рядом. При х=х0 ряд перетворюється на числовий. Степеневим рядом, називається функціональний ряд вигляду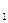 х +a
х +a  X2+...+ а
X2+...+ а  x
x  +...=
+...= 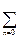 а
а  , a
, a  a
a  (х-х
(х-х 
 нескінченно диференційована в деякому околі точки
нескінченно диференційована в деякому околі точки  тоді ряд
тоді ряд  має назву ряда Тейлора функції
має назву ряда Тейлора функції  у точці
у точці  . У випадку, якщо
. У випадку, якщо  цей ряд іноді зветься рядом Маклорена.
цей ряд іноді зветься рядом Маклорена. Якщо ряд збігається, то його сума дорівнює періодичній функції
Якщо ряд збігається, то його сума дорівнює періодичній функції  з періодом
з періодом  , оскільки
, оскільки  та
та  є періодичними з періодом
є періодичними з періодом 
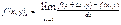 22. Поняття функції багатьох змінних.Границя та неперервність функції.Частинні похідні функції. Множина значень {x1,…,xn}, за яких вираз f(x1,…,xn) має зміст, називається областю визначення функції від n змінних y = f(x1,…,xn). Частинною (частковою) похідною від функції f (x, y) за аргументом x називається границя
22. Поняття функції багатьох змінних.Границя та неперервність функції.Частинні похідні функції. Множина значень {x1,…,xn}, за яких вираз f(x1,…,xn) має зміст, називається областю визначення функції від n змінних y = f(x1,…,xn). Частинною (частковою) похідною від функції f (x, y) за аргументом x називається границя Для частинних похідних від функції f (x, y) використовують такі позначення: f ¢x(x, y); z ¢x
Для частинних похідних від функції f (x, y) використовують такі позначення: f ¢x(x, y); z ¢x f ¢y(x, y); z ¢y
f ¢y(x, y); z ¢y де
де  та
та  — функції, що залежать тільки від аргументу x.
— функції, що залежать тільки від аргументу x. того, що подія
того, що подія  настане
настане  разів в
разів в  незалежних випробуваннях дорівнює
незалежних випробуваннях дорівнює  або
або




