
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мішаний добуток трьох векторів та його властивості . Об’єм паралелепіпеда , заданого координатами векторів на яких він лежитьСтр 1 из 2Следующая ⇒
Опис методу Для системи
з визначником матриці системи
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів). Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:
У такій формі формула Крамера справедлива без припущення, що Метод Гаусса розв¢язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь до трикутного вигляду 4. Означення матриці. Види матриць.Дії над матрицями. Обернена матриця. Озн. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Числа aij називають елементами матриці, а запис m x n – розмірністю матриці. Якщо кількість рядків і стовпчиків матриці збігаються, то матриця називається квадратною. Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю, називається одиничною матрицею. Якщо всі елементи матриці, що знаходяться по один бік від головної діагоналі, дорівнюють нулю, то матриця називається трикутною. Кожній квадратній мватриці можна поставити у відповідність визначник, який складається з тих самих елементів. Якщо такий визначник відмінний від нуля, то матриця називається неособливою (невиродженою). Якщо визначник дорівнює нулю, то матриця особлива (вироджена). Дії над матрицями. Сумою матриць одного порядку A=(aij) i B=(bij) називається матриця С=А+В; С=(cij) будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В: Cij=aij+bij. Добутком матриці A=(aij) на деяке число_ називається така матриця С, кожен елемент якої Cij одержується множенням відповідних елементів матриці А на, Cij= _ x Aij. Добутком матриці A=(Aij) розмірності m x p на матрицю B=(Bij) розмірності p x n називається така матриця С=А х В розмірністю m x n, C=(Cij)
Прямокутна система координат на площині та в просторі. Векторні величини. Дії над векторами. Розклад вектора за базисом.Координати та довжина вектора Скалярний добуток векторів. Кут між векторами. Прямокутна система координат у просторі утворюється трьома взаємно перпендикулярними осями координат O X, O Y і O Z. Осі координат перетинаються в точці O, Яка називається початком координат, на кожній осі вибрано позитивне напрямок, вказаний стрілками, і одиниця виміру відрізків на осях. O X - вісь абсцис, O Y - вісь ординат, O Z - вісь аплікат Векторні величини Вектор — у фізиці і математиці - величина, яка характеризується числовим значенням і напрямкомГрафічно вектори зображають у вигляді напрямлених відрізків певної довжини Дії над векторами
Сумою двох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить з цієї ж точки. Віднімання векторів Щоб відняти два вектори, потрібно відкласти їх від спільної точки, з'єднати кінці і стрілку поставити до того вектора, від якого віднімаємо Скалярний добуток векторів. Скалярним добутком двох векторів називають число, що дорівнює добутку довжин цих векторів на косинус кута між ними.
6. Векторний добуток двох векторів і його властивості.Площа паралелограма та трикутника заданими координатами вершин. Векторним добутком двох векторів 1) Довжина вектора 2) Вектор 3) Вектори
Рівняння прямої з напрямним вектором. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, що проходить через дві точки. Рівняння прямої, що проходить через задану точку перпендикуляр до заданого вектора. -Рівняння прямої з кутовим коефіцієнтом Загальне рівняння прямої коли B≠0 можна привести к вигляду у=кх+в, де k- кутовий коефіцієнт, який дорівнює тангенсу кута, утвореного даною прямою і додатним напрямком осі ОХ Рівняння прямої, що проходить через дві різні точки на площині. Якщо пряма проходить через дві точки A(x1, y1) і B(x2, y2), такі що x1 ≠ x2 і y1 ≠ y2 то рівняння прямої можна знайти, використовуючи наступну формулу Загальне рівняння площини Будь-яку площину можна задати рівнянням площини першого ступеня виглядуA x+ B y+ C z+ D= 0 де A, B і C не можуть одночасно дорівнювати нулю. Кут між площинами дорівнює куту між прямими, що перпендикулярні цим площинам, і знаходиться в межах від 0° до 90°. Якщо задане рівняння прямої Ax+ By+ C = 0, то відстань від точки M(Mx, My) до прямої можна знайти, використавши наступну формулу Збіжності ряду 21. Ряди Тейлора та Маклорена. Тригонометричний ряд Фур’є Нехай функція Тригонометричним рядом Фур'є називають функційний ряд виду
Частинну (часткова) похідну від функції f (x, y) за аргументом y визначають аналогічно.
23. Скалярне поле. Похідна за напрямом. Градієнт Скалярним полем - називають називають частину простору(увесь простір), у кожній точці якого відповідно до певного закону задано числове значення деякої скалярної величини. Похідна за напрямком - це узагальнення поняття похідної на випадок функції кількох змінних. Похідна за напрямом показує, наскільки швидко функція змінюється при русі вздовж заданого напряму. Градієнт — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Диференціальні рівняння, основні означення.Рівняння з відокремлюваними змінними,однорідні, в повних диференціалах. Лінійні диференціальні рівняння першого та другого порядку.Рівняння вищих порядків. Диференціальне рівняння — це рівняння, в якому невідомою величиною диференціал Рівняння вигляду P (x) dx + Q (y) dy =0. називається рівнянням з відокремленими змінними. Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду 26 Основні поняття комбінаторики. Правила комбінаторики Випадкова подія — подія, яка при заданих умовах може як відбутись, так і не відбутись, при чому існує визначена ймовірність того, що вона відбудеться при заданих умовах. Ймові́рність — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів.
27. Ймовірність події. Класифікація подій. Операції над подіями Ймові́рність — числова характеристика можливості того, що випадкова подія відбудеться в умовах, які можуть бути відтворені необмежену кількість разів. Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню. Подія — результат випробування. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною і позначається літерою U. Подія, яка в даному випробуванні не може відбутись, називається неможливою і позначається літерою V. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. 28. Послідовність незалежних випробувань.Формули Бернуллі, Пуассона У теорії ймовірності, формула Бернуллі дозволяє обчислити ймовірність успіхів у серії незалежних експериментів. Якщо ймовірність Р настання події А в кожному з випробувань стала, то ймовірність
Формула Пуассона Якщо ймовірність p настання події А в кожному випробуванні постійна, близька до нуля, а число незалежних випробувань n досить велике, то імовірність Pn (k) того, що в n незалежних випробуваннях подія А наступить k разів, наближено дорівнює: Опис методу Для системи
з визначником матриці системи
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів). Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:
У такій формі формула Крамера справедлива без припущення, що
Метод Гаусса розв¢язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь до трикутного вигляду 4. Означення матриці. Види матриць.Дії над матрицями. Обернена матриця. Озн. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Числа aij називають елементами матриці, а запис m x n – розмірністю матриці. Якщо кількість рядків і стовпчиків матриці збігаються, то матриця називається квадратною. Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю, називається одиничною матрицею. Якщо всі елементи матриці, що знаходяться по один бік від головної діагоналі, дорівнюють нулю, то матриця називається трикутною. Кожній квадратній мватриці можна поставити у відповідність визначник, який складається з тих самих елементів. Якщо такий визначник відмінний від нуля, то матриця називається неособливою (невиродженою). Якщо визначник дорівнює нулю, то матриця особлива (вироджена). Дії над матрицями. Сумою матриць одного порядку A=(aij) i B=(bij) називається матриця С=А+В; С=(cij) будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В: Cij=aij+bij. Добутком матриці A=(aij) на деяке число_ називається така матриця С, кожен елемент якої Cij одержується множенням відповідних елементів матриці А на, Cij= _ x Aij. Добутком матриці A=(Aij) розмірності m x p на матрицю B=(Bij) розмірності p x n називається така матриця С=А х В розмірністю m x n, C=(Cij) Прямокутна система координат на площині та в просторі. Векторні величини. Дії над векторами. Розклад вектора за базисом.Координати та довжина вектора Скалярний добуток векторів. Кут між векторами. Прямокутна система координат у просторі утворюється трьома взаємно перпендикулярними осями координат O X, O Y і O Z. Осі координат перетинаються в точці O, Яка називається початком координат, на кожній осі вибрано позитивне напрямок, вказаний стрілками, і одиниця виміру відрізків на осях. O X - вісь абсцис, O Y - вісь ординат, O Z - вісь аплікат Векторні величини Вектор — у фізиці і математиці - величина, яка характеризується числовим значенням і напрямкомГрафічно вектори зображають у вигляді напрямлених відрізків певної довжини Дії над векторами
Сумою двох не колінеарних векторів, що виходять з однієї точки, є діагональ паралелограма, побудованого на цих векторах, яка виходить з цієї ж точки. Віднімання векторів Щоб відняти два вектори, потрібно відкласти їх від спільної точки, з'єднати кінці і стрілку поставити до того вектора, від якого віднімаємо Скалярний добуток векторів. Скалярним добутком двох векторів називають число, що дорівнює добутку довжин цих векторів на косинус кута між ними.
6. Векторний добуток двох векторів і його властивості.Площа паралелограма та трикутника заданими координатами вершин.
Векторним добутком двох векторів 1) Довжина вектора 2) Вектор 3) Вектори
Мішаний добуток трьох векторів та його властивості.Об’єм паралелепіпеда, заданого координатами векторів на яких він лежить Розглянемо добуток векторів, складений в такий спосіб: перші два вектори перемножуються, а їхній результат множимо на третій вектор. Такий добуток називається векторно-скалярним, або мішаним добутком трьох векторів. Мішаний добуток являє собою деяке число.
Рівняння прямої з напрямним вектором. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, що проходить через дві точки. Рівняння прямої, що проходить через задану точку перпендикуляр до заданого вектора. -Рівняння прямої з кутовим коефіцієнтом Загальне рівняння прямої коли B≠0 можна привести к вигляду у=кх+в, де k- кутовий коефіцієнт, який дорівнює тангенсу кута, утвореного даною прямою і додатним напрямком осі ОХ Рівняння прямої, що проходить через дві різні точки на площині. Якщо пряма проходить через дві точки A(x1, y1) і B(x2, y2), такі що x1 ≠ x2 і y1 ≠ y2 то рівняння прямої можна знайти, використовуючи наступну формулу
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.107 (0.056 с.) |
 лінійних рівнянь з
лінійних рівнянь з 
 , що не рівний нулю, розв'язок записується у такому вигляді:
, що не рівний нулю, розв'язок записується у такому вигляді:

 та
та  , або набір
, або набір  складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.
складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями.
 Додавання векторів Правило трикутника
Додавання векторів Правило трикутника Правило паралелограма
Правило паралелограма
 , де
, де 
 і
і  називається вектор
називається вектор  , який задовольняє таким умовам:
, який задовольняє таким умовам: дорівнює площі паралелограма, побудованого на векторах
дорівнює площі паралелограма, побудованого на векторах  і
і 
 перпендикулярний до площини цього паралелограма, тобто перпендикулярний і до вектора
перпендикулярний до площини цього паралелограма, тобто перпендикулярний і до вектора  :
:  та
та 
 ,
,  ,
,  , взяті у такому порядку, утворюють праву трійку векторів. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки.
, взяті у такому порядку, утворюють праву трійку векторів. Упорядкована трійка некомпланарних векторів називається правою, якщо з кінця третього вектора найкоротший поворот від першого вектора до другого здійснюється проти обертання годинникової стрілки.

 нескінченно диференційована в деякому околі точки
нескінченно диференційована в деякому околі точки  тоді ряд
тоді ряд  має назву ряда Тейлора функції
має назву ряда Тейлора функції  у точці
у точці  . У випадку, якщо
. У випадку, якщо  цей ряд іноді зветься рядом Маклорена.
цей ряд іноді зветься рядом Маклорена. Якщо ряд збігається, то його сума дорівнює періодичній функції
Якщо ряд збігається, то його сума дорівнює періодичній функції  з періодом
з періодом  , оскільки
, оскільки  та
та  є періодичними з періодом
є періодичними з періодом 
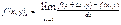 22. Поняття функції багатьох змінних.Границя та неперервність функції.Частинні похідні функції. Множина значень {x1,…,xn}, за яких вираз f(x1,…,xn) має зміст, називається областю визначення функції від n змінних y = f(x1,…,xn). Частинною (частковою) похідною від функції f (x, y) за аргументом x називається границя
22. Поняття функції багатьох змінних.Границя та неперервність функції.Частинні похідні функції. Множина значень {x1,…,xn}, за яких вираз f(x1,…,xn) має зміст, називається областю визначення функції від n змінних y = f(x1,…,xn). Частинною (частковою) похідною від функції f (x, y) за аргументом x називається границя Для частинних похідних від функції f (x, y) використовують такі позначення: f ¢x(x, y); z ¢x
Для частинних похідних від функції f (x, y) використовують такі позначення: f ¢x(x, y); z ¢x f ¢y(x, y); z ¢y
f ¢y(x, y); z ¢y де
де  та
та  — функції, що залежать тільки від аргументу x.
— функції, що залежать тільки від аргументу x. того, що подія
того, що подія  настане
настане  разів в
разів в  незалежних випробуваннях дорівнює
незалежних випробуваннях дорівнює  або
або




