
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тестуваннагетероскедастичності залишків
Ще один тест для перевірки гетероскедастичності запропонував Глейсер: розглядати регресію абсолютних значень залишків 1) 2) 3) Рішення про відсутність гетероскедастичності залишків приймається на основі статистичної значущості коефіцієнтів
Якщо при економетричному моделюванні для певних вихідних даних буде виявлено явище гетероскедастичності, то оцінку параметрів моделі треба виконувати на основі узагальненого методу найменших квадратів. Оператор оцінювання цим методом запишеться:
де
В даній матриці залежно від висунутої гіпотези: або або або Прогноз на основі економетричної моделі, в якій оцінка параметрів виконана узагальненим методом найменших квадратів, можна отримати на основі такого співвідношення:Ω-1
де u — вектор залишків, який відповідає оцінці параметрів моделі на основі 1МНК;
17. Узагальнений метод найменших квадратів (метод Ейткена) Оператор оцінювання УМНК можна записати так:
де Ω-1-матриця, обернена до дисперсійно-коваріаційної матриці залишків Ω.
На практиці для розрахунку ρ використовується співвідношення
Економетрична модель, якійпритаманнагетероскедастичність, є узагальненоюмоделлю, і для оцінюванняїїпараметрівслідскористатисяузагальненим методом найменшихквадратів. Розглянемоцей метод. Нехай задано економетричну модель
коли Задача полягає в знаходженніоцінокелементів вектора А в моделі. Для цьоговикористовуєтьсяматриця S, за допомогоюякоїкоригуєтьсявихіднаінформація. Цяідеябулапокладена в основу методу Ейткена. Базуючись на особливостяхматриць Р і S, якібулирозглянуті в підрозд. 7.3, можназаписатиспіввідношенняміжцимиматрицями та оберненими до них.
Оскільки S — додатновизначенаматриця, то вона може бути зображена як добуток
Помноживши рівняння (7.1) ліворуч на матрицю
Позначимо
Тоді модель матимевигляд:
Використовуючи (7.3), неважкопоказати, що
тобто модель (7.6) задовольняєумови (4.2), коли параметримоделіможнаоцінити на основі 1МНК. Звідси
Цяоцінка є незміщеноюлінійноюоцінкою вектора А, якиймаєнайменшудисперсію і матрицюковаріацій
Hезміщенуоцінку для дисперсії
Оцінкапараметрів При заданійматриці S оцінкупараметрівмоделіможнаобчислитизгідноіз (7.7), а стандартнупомилку — згідноіз (7.8). Тому можнасконструюватизвичайнікритеріїзначущості і довірчіінтервали для параметрів Визначившизалишки
або Звідси Тоді Оскільки то Отже, ми розбилизагальну суму квадратів для (7.6) на суму квадратіврегресії і залишкову. Згідно з цимиданимидисперсійнийаналіз буде виконано для перетворенихвихіднихданих. Крім того, коли незалежназмінна Модель узагальненого методу найменшихквадратівінодіспецифікується у вигляді
де
а для їїковаріаційноїматриці
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 168; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.51.241 (0.007 с.) |
 , які відповідають регресії найменших квадратів як деяку функцію від
, які відповідають регресії найменших квадратів як деяку функцію від  , де
, де  є тією незалежною змінною, яка відповідає зміні дисперсії
є тією незалежною змінною, яка відповідає зміні дисперсії  . Для цього використовуються такі види функцій:
. Для цього використовуються такі види функцій: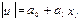 ;
; ;
; і т.п.
і т.п. й
й 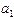 . Переваги цього тесту визначаються можливістю розрізняти випадок чистої і змішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів
. Переваги цього тесту визначаються можливістю розрізняти випадок чистої і змішаної гетероскедастичності. Чистій гетероскедастичності відповідають значення параметрів  ,
,  ; а змішаній —
; а змішаній — 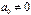 ,
,  . Залежно від цього треба користуватись різними матрицями
. Залежно від цього треба користуватись різними матрицями  . Нагадаємо, що:
. Нагадаємо, що: .
. ,
, .
. ;
; ;
; .
. ,
,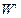 — транспонований вектор коваріацій поточних і прогнозних значень залишків;
— транспонований вектор коваріацій поточних і прогнозних значень залишків; , а
, а 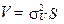 .
.

 або
або 
 (7.1)
(7.1) .
.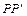 , де матриця P є невиродженою, тобто:
, де матриця P є невиродженою, тобто: , (7.2) коли
, (7.2) коли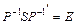 ; (7.3) і
; (7.3) і . (7.4)
. (7.4) ,дістанемо:
,дістанемо: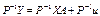 . (7.5)
. (7.5) ;
;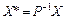 ;
; .
. . (7.6)
. (7.6) ,
, . (7.7)
. (7.7) (7.8)
(7.8) можнадістати так:
можнадістати так: (7.9)
(7.9) , яку знайдено за допомогою (7.7), є оцінкоюузагальненого методу найменшихквадратів (методу Ейткена).
, яку знайдено за допомогою (7.7), є оцінкоюузагальненого методу найменшихквадратів (методу Ейткена). .
. і помноживши ліворуч на матрицю
і помноживши ліворуч на матрицю  , дістанемо:
, дістанемо: ,
, .
. .
. .
. ,
, (7.10)
(7.10) вимірянавідносно початку відліку, а не у формівідхиленнявідсередньої, то необхідновизначитиїїсереднєзначення і скористатись ним для корекціїзагальноїсумиквадратів і сумиквадратіврегресії.
вимірянавідносно початку відліку, а не у формівідхиленнявідсередньої, то необхідновизначитиїїсереднєзначення і скористатись ним для корекціїзагальноїсумиквадратів і сумиквадратіврегресії.
 (7.11)
(7.11)
 —відомасиметричнадодатновизначенаматриця. Тодівираз для оцінкипараметрівзгідно з методом Ейткеназапишеться так:
—відомасиметричнадодатновизначенаматриця. Тодівираз для оцінкипараметрівзгідно з методом Ейткеназапишеться так: , (7.12)
, (7.12) . (7.13)
. (7.13)


