
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямая и плоск. Т. пересеч. прямой и плоск. Угол м-у прямой и плоск. Услов. паралл-ти и перп-ти прямой и плоск. ⇐ ПредыдущаяСтр 4 из 4
Коорд. т. пересеч. прямой L и плоск. α должны одноврем. удовл. ур-ям:
Подставляя их в ур-е плоск, получ. знач. парам. t
Подставляя найд. t в парам. ур-я прямой, получ. корд. т. пересеч. прямой и плоск.
L L||α ó
Эллипс Эллипсом назыв. геом. место точек M(x;y), для кот. сумма расстояний до 2-х зад. т. F1(c;0),F2(-с;0), назыв. фокусами эллипса, постоянна и равна 2а. По опр-ю | | Восп-ся форм-ми расст. м-у 2-мя т: | r1+r2=2a
т.к a>c,
x2/a2 + y2/b2 =1 - канонич. ур-е эллипса Эл-ты эллипса: О – центр эллипса, ABCD – вершины эллипса F1(c;0), F2(-с;0) - фокусы эллипса 2с - фокусное расстояние, кот. вычисл. по ф-ле с= AC=2a, BD=2b - большая и малая полуоси эллипса Ɛ=с/a (Ɛ <1) - эксцентриситет эллипса, Ɛ = Эксцентриситет опр-ся отношением осей эллипса и характериз.т его форму. Прямые, парал. малой оси и отстоящие от нее на расстояние a/Ɛ, назыв. директрисами эллипса. Ур-е директрисы: X=±a/ Ɛ; a/ Ɛ >a т.е Ɛ <1 Фокальный параметр P= Окружность предст. собой геом. место точек, равноудал. от т. О, назыв. центром окружн-ти, a=b=п
Гипербола Гиперболой назыв. геом. место точек M(x;y), для кот. абсол. величина разности расстояний до 2-х зад. т. F1(c;0),F2(-с;0), назыв. фокусами гиперболы, постоянна и равна 2а (a<c) По опр-ю | Найдем:| |r1-r2|=2a; r1-r2=±2a
X2/a2 - y2/b2 =1 - канонич. ур-е гиперболы Эл-ты гиперболы: О – центр гиперболы, A,B – вершины гиперболы F1(c;0),F2(-с;0) – фокусы гиперболы 2с - фокусное расстояние, кот. вычисл. по ф-ле AB=2a – действит.. ось гиперболы. СD=2b – мнимая ось гиперболы Ɛ=с/a - эксцентриситет гиперболы, Ɛ = Эксцентритет опр-ся отношением осей гиперболы и характеризует ее форму: чем больше эксцентриситет, тем более вытянут вдоль мнимой оси основной прямоуг-к гиперболы. Ур-я директрис имеют вид: х=±a/Ɛ; т.к Ɛ >1 то a/Ɛ <a Асимптоты гиперболы – это прямые, к кот. ветви гиперболы неограниченно приближаются при удалении на бесконечность
k=±tgα=±b/a y=kx=± Фокальный параметр P=
Парабола Параболой назыв. геом. место точек M(x;y), равноудаленных от зад. т. F( Канонич. ур-е параболы м.б. получ. из опр-я: F(
Эл-ты параболы: О- вершина параболы ОХ – ось параболы F( х= - p – фокальный параметр (расстояние от фокуса до директрисы или половина хорды, проходящ. ч-з фокус перпенд. оси ОХ)
Поверхн. 2-го пор. Поверхн. вращ-я. Циллиндрич. поверхн. Конич. поверхн. 2-го пор. Поверхн. 2-го пор. — геом-е место точек, декартовы прямоуг. коорд. кот. удовл. ур-ю вида a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (1), в кот. по крайней мере один из коэф-ов a11, a22, a33, a12, a23, a13 отличен от 0. Ф-ла (1) сост. из квадратичн. формы, линейн. формы и своб. члена. Th. Ур-е (1) предст. собой геом-ки либо эллипсоид, либо параболоид, либо гиперболу, либо конус, либо цилиндр и ничего больше, если не счит. вырожденных случаев.
Пусть F(X,Y)=0 – нек. кривая плоск. Z=0. Будем вращ. эту кривую вокруг оси OX. В результ. получ. поверхн. вращ-я. Пусть т. М1(Х,У,0) – произв. т. на кривой и при вращении она опишет окружн. радиуса R=|Y|. Пусть т. М(х,у,z) – т. окружн (поверх-ти вращ-я). При этом x=X, R=|Y|= Подставл. в ур-е F(X,Y)=0 найд. знач. X, Y, получ. ур-е поверх. вращ-я F( Замечание: Если кривую вращ. вокруг оси ОУ, то, чтобы получ. ур-е поверхн. вращ-я, след. в ур-ии кривой F(X,Y)=0 оставить без измен. переем. Y, а перем. Х замен. на F( Если ур-е f(x;y)=0 (в плоск. z=0) зад. нек. кривую, то это же ур-е в простр. явл. цилиндрич. поверхн-ю. x2/a2 + y2/b2 =1 – эллиптич. цилиндр x2/a2 - y2/b2 =1 – гиперболич. цилиндр y2=2px – параболич. цилиндр Если вращать прямую вокруг оси OZ получ. конич. поверхн. z=±k* z2=k2(x2+y2) z2= Обобщая, получ. z2=
Эллипсоид Будем вращать эллипс x2/a2 + y2/b2 =1 вокруг OУ. Согл. ф-ле (F(±
Обобщая, получ. При a=b=c=R получ. ур-е сферы x2+y2+z2=R2
Если рассек. эллипсоид плоскостями, перпенд. осям коорд, то все ее сечения будут эллипсами
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.221.136 (0.039 с.) |




 - угол м-у прямой и плоск,
- угол м-у прямой и плоск,  ,
,  ||L
||L



 – угол м-у прямой и плоск.
– угол м-у прямой и плоск. α ó
α ó  ||
||  ó
ó 
 ó
ó 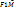 |+|
|+|  |=2a,
|=2a,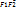 |=2c, a>c
|=2c, a>c =
=  ; |
; |  =
= 

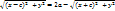


 :возводим в квадрат и группируем
:возводим в квадрат и группируем





 .
. - это половина хорды, провед. ч-з фокус, параллельно малой оси.
- это половина хорды, провед. ч-з фокус, параллельно малой оси. – ур-е окружн. с центром (x0,y0) и радиусом r.
– ур-е окружн. с центром (x0,y0) и радиусом r.  – канонич. ур-е окружн.
– канонич. ур-е окружн. |=2a, |
|=2a, |  |=
|= 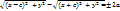



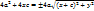


 *(-1)
*(-1)
 , т.к. по услов. C>a
, т.к. по услов. C>a


 *x – ур-я асимптоты
*x – ур-я асимптоты
 ;0) и от данной прямой, назыв. директрисой параболы
;0) и от данной прямой, назыв. директрисой параболы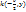 , M(x,y), FM=MK,
, M(x,y), FM=MK, 

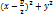 =
= 
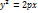
 (
( ) – квадратичная форма n-го пор.
) – квадратичная форма n-го пор. , у=
, у= 
 )=0
)=0
 )=0
)=0
 - коническая поверхность
- коническая поверхность 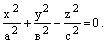
 – эллиптич. коническая поверхн.
– эллиптич. коническая поверхн.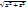 ;y)=0) получим след. ур-е поверхн.
;y)=0) получим след. ур-е поверхн. – эллипсоид вращ-я, a,b –полуоси эллипсоида вращения.
– эллипсоид вращ-я, a,b –полуоси эллипсоида вращения. - ур-е эллипсоида, где все полуоси a,b,c-разные.
- ур-е эллипсоида, где все полуоси a,b,c-разные.


