
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расст. М-у 2-мя Т. Деление отрезка в данном отнош-ии. Прямая линия на плоск. Осн. Виды ур-я прямой на плоск.
Общ. ур-е прямой на плоск. XOY получ. из общ. ур-я плоск. в пр-ве при Z=0. L: Ax+By+C=0 – прямая на плоск в ДСК С=0: прямая прох. ч-з начало корд., A=0: L||OX,,B=0: L||OY
Пусть прямая L прох. ч-з т. M(x0,y0),
Пусть M1(x1,y1), M2(x2,y2)
Пусть L сост. с осью OX (полож. направл.) угол Прямая м.б. задана т. М1(x1,y1) и k=tg Из общ. ур-я прямой Ax+By+C=0 при Из ур-я прямой, проходящ. ч-з 2 т. имеем:
Из норм-го ур-я плоск. при z=0 получ. норм. ур-е прямой на плоск: Его можно получ. из общ. ур-я прямой, домножив на µ:
Расст. от т. до прямой. Коорд. т. пересеч. двух прямых. Угол м-у двумя прямыми. Услов. паралл-ти и перп-ти прямых d=|δ| - модуль отклонения т. от прямой
δ>0 - если М0 и нач. коорд-т по разные стороны от прямой
Угол м-у двумя прямыми L1: y=k1x+b1, L2: y=k2x+b2
Если прямые зад. общими ур-ми: L1: A1x+B1y+C1=0, L2: A2x+B2y+C2=0
Услов. паралл-ти и перп-ти прямых Пусть L1: y=k1x+b1, L2: y=k2x+b2 L1 || L2 ó k1=k2, L1 ┴ L2: ó k1k2=-1 (ϕ=90*) Если L1: A1x+B1y+C1=0, L2: A2x+B2y+C2=0
L1┴L2 ó A1A2+B1B2=0 Плоск. в пр-ве. Основн. виды ур-й плоск. в пр-ве. Услов паралл-ти и перп-ти плоск. М0(x0,y0,z0) – фиксир. т. плоск., M(x,y,z) – текущ. т. плоск.,
A(x-x0)+B(y-y0)+C(z-z0)=0 – ур-е плоск., проход. ч- з т. М(х0,у0,z0) и вектором нормали Ax+By+Cz+D=0 - общее ур-е плоскости Следствие: Если 2 ур-я A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 опред. одну и ту же плоск., то Пусть плоск. не прох. ч-з нач. корд. Ax+By+Cz+D=0, Ax+By+Cz=-D,
Пусть М(x,y,z) – произв. т. плоск.
Приведение общ. ур-я к норм. виду Т.к.
Замечание 1. Приведение ур-я плоск. к норм-му виду позв. узнать ее расположение отн-но сист. коорд. Замечание 2. Введение нормир-го множителя соотв-т замене произв. вектора нормали
Неполные ур-я плоск. Расст. от т. до плоск. Если в общ. ур-ии плоск. отсутств. какие-то слагаемые, то оно назыв. неполным. D=0: Ax+By+Cz=0 плоск. проходит ч-з начало корд. A=0: By+Cz+D=0 => B=0: Ax+Cz+D=0 => C=0: Ax+Bx+D=0 => A=0, B=0: Cz+D=0 => A=0, C=0: By+D=0 => B=0, C=0: Ax+D=0 => A=0, B=0, D=0: Cz=0 => A=0, С=0, D=0: By=0 => B=0, C=0, D=0: Ax=0 => Пусть M1(x1,y1,z1), проекция вект. Отклонением δ т. М1(x1,y1,z1) от плоск. назыв. число, равное длине перпендикуляра опущ. из т. М1 на плоск., взятое со знаком “-“, если т. М1 и нач.корд. по одну сторону от плоск., и ”+” по разные. Чтобы найти δ т., нужно в лев. часть норм. ур-я этой плоск. подставить корд. этой т: Если плоскость зад. общим ур-ем, то:
Расстояние от т. М1(x1,y1,z1) до плоск.
Ур-е плоск, прох. ч-з 3 данных т. Угол м-у плоск. M(x,y,z) – текущ. т. плоск, M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3) Т. М лежит в плоск. М1М2М3 только в том случ., если векторы М1М, М1М2, М1М3 – компл. ó
Пусть 2 плоск. зад. общими ур-ми:
Угол м-у плоск. опр-ся как угол м-у их норм. векторами n1 и n2:
Прям. линия в простр. Основн. виды ур-я прямой линии в простр. Угол м-у прямыми. Услов. паралл-ти и перп-ти 2-х прямых. M0(x0,y0,z0) – фиксир. т. прямой L, M
M(x,y,z) – произв. т. прямой L. M
Исключ. параметр t:
Пусть даны 2 т. M1(x1,y1,z1), M2(x2,y2,z2). Вектор
Пусть
Пусть прямая L зад. линией пересеч. 2-х плоск:
Совокупность всех плоскостей, прох. ч-з одну и ту же прямую, назыв. пучком плоскостей.
Пусть зад. направл. векторы 2-х прямых Угол м-у прямыми приним. равным углу м-у направл-ми векторами: L1||L2ó L1
|
||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.48 (0.023 с.) |
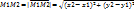 – расст. м-у 2-мя т. M1(x1,y1), M2(x2,y2)
– расст. м-у 2-мя т. M1(x1,y1), M2(x2,y2) (A;B),
(A;B),  , то
, то – канонич. ур-е прямой на плоск.
– канонич. ур-е прямой на плоск.
 , парам. ур-е прямой
, парам. ур-е прямой – ур-е прямой, прох. ч-з 2 т.
– ур-е прямой, прох. ч-з 2 т. .
. , М1(x1,y1), M2(x2,y2)
, М1(x1,y1), M2(x2,y2) получ. ур-е прямой с углов. коэф. k:
получ. ур-е прямой с углов. коэф. k: 


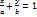 - ур-е прямой в отрезках (перес. ОХ в А(а;0) В(0;b))
- ур-е прямой в отрезках (перес. ОХ в А(а;0) В(0;b)) ,
, 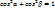 ,
, 


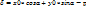

 расст. от М0(х0;у0) до прямой
расст. от М0(х0;у0) до прямой - коорд. т. пересеч. прямых
- коорд. т. пересеч. прямых
 =>
=> 
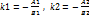



 – вектор нормали,
– вектор нормали, 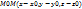

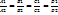 Если
Если 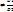 то плоск. парал.
то плоск. парал. ,
, ,
, 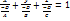
 – уравнение пл-ти в отрезках, где
– уравнение пл-ти в отрезках, где 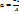 ,
,  ,
,  – корд. т. пересеч. плоск. с коорд-ми осями и равны отрезкам, отсекаемым плоск-ю на коорд-х осях
– корд. т. пересеч. плоск. с коорд-ми осями и равны отрезкам, отсекаемым плоск-ю на коорд-х осях (x,y,z) – коорд. радиус-вектора. P – основн. перп., опущ. из нач. корд. на плоск. |
(x,y,z) – коорд. радиус-вектора. P – основн. перп., опущ. из нач. корд. на плоск. |  |=p,
|=p,  ,
, 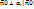 =1 – единичн. вектор нормали к плоск.
=1 – единичн. вектор нормали к плоск. 




 =>
=> =>
=>  – норм. ур-е плоск., где cosα, cosβ, cosγ – направл. косинусы нормали к плоск., р – расст-е от нач. коорд-т до плоск.
– норм. ур-е плоск., где cosα, cosβ, cosγ – направл. косинусы нормали к плоск., р – расст-е от нач. коорд-т до плоск.

 =>
=> 
 – нормирующий множитель
– нормирующий множитель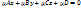 – нормальный вид
– нормальный вид (A,B,C) в ур-ии плоск. на единич. вектор нормали
(A,B,C) в ур-ии плоск. на единич. вектор нормали  =
=  =(cosα,cosβ,cosγ)
=(cosα,cosβ,cosγ)











 ) Спроектируем т. М1 на нормаль
) Спроектируем т. М1 на нормаль  на
на  =p
=p  δ=(проекция вект.
δ=(проекция вект. 


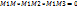
 – ур-е плоск., прох. ч-з 3 т.
– ур-е плоск., прох. ч-з 3 т.


 L,
L,  ||L, a(l,m,n)
||L, a(l,m,n) Ló
Ló  ||
|| 
 - векторное ур-е прямой
- векторное ур-е прямой – парам. ур-е прямой
– парам. ур-е прямой – канонич. ур-е прямой, проход. ч-з фиксир. т. M0(x0,y0,z0) и имеющей направл. вектор
– канонич. ур-е прямой, проход. ч-з фиксир. т. M0(x0,y0,z0) и имеющей направл. вектор  выбер. в кач-ве направл. прямой L, тогда ур-е прямой примет вид:
выбер. в кач-ве направл. прямой L, тогда ур-е прямой примет вид: - ур-е прямой, проходящей ч-з 2 т.
- ур-е прямой, проходящей ч-з 2 т. ,
,  , α1||α2
, α1||α2  , в противн. случ. плоск. пересек. и прямая пересечения плоск опр-ся ур-ем:
, в противн. случ. плоск. пересек. и прямая пересечения плоск опр-ся ур-ем: – общее ур-е прямой
– общее ур-е прямой
 ,
,  - это рав-во опр. плоск., кот. прох. ч-з прямую L.
- это рав-во опр. плоск., кот. прох. ч-з прямую L. ,
,  – опред. все плоскости пучка, кроме 2-й из задающих прямую.
– опред. все плоскости пучка, кроме 2-й из задающих прямую. ||
||  ,
,  ||
||  ,
, 
 ó
ó 
 L2ó
L2ó  ó
ó 



