
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие вектора и лин. Опер. Над вект-ми. Св-ва опер. Слож. Вект-ов и умнож. Вект-а на число (с док-вом)Стр 1 из 4Следующая ⇒
Понятие вектора и лин. опер. над вект-ми. Св-ва опер. слож. вект-ов и умнож. вект-а на число (с док-вом) Величины, для опр-я кот. дост-но знать одно число, назыв. скаляром. Геом. вектором назыв. направл. отрезок (характ-ся длиной (модулем) и направл-ем). Своб. векторы счит. равным и, если модули равны и направл. одинак. Вектора не явл. своб., если сущ. т. приложения вектора или линия действия вектора (связанные и скользящие.) Длиной вектора назыв. расстояние от нач. к концу вектора. Нулевым вектором назыв. вектор, у кот. начало и конец совпад. Векторы назыв. коллинеарными, если лежат на одной прямой, либо на парал. прямых. Нулевой вектор коллинеарен люб. вектору. 3 вектора назыв. компланарными, если они лежат в одной плоск., либо в парал. плоск-ях. Если тройка векторов содерж. нулевой вектор или пару коллинеарн. векторов, то эти векторы комплан. Два вектора равны, если они коллинеарны, имеют одинак. длину и направл-е. Линейные операции 1. Суммой векторов Св-ва: 1. 2. ( 3. (Ǝ 4. Правило парал-ма: Если Вычитание 1 сп. 2 сп. 3. Произведение Св-ва: 1. k*( 2. 3. λ*(β* 4. 1*
1. Д-ва: 1. ABCD – парал-м, ( 2.
3. Д-во вытек. из опр-й суммы векторов и нулевого вектора. 4. Дост-но опр. 3. Д-ва: 1. ----- 2. ----- 3. ----- 4.-----
+ док-ва и графики на обратн. сторону Линейн. зависимость векторов (опред-е, св-ва с док-вом) Линейной комбинацией векторов Векторы
Векторы Св-ва: 1. Если сист. векторов содерж. 2. Если среди n векторов какие-либо (n-1) ЛЗ, то и все n векторов ЛЗ. 3. ----- 4. ----- 5. ----- 6. ----- 7. ----- Д-ва: 1. ----- 2. ----- 3. ----- 4. ----- 5. ----- 6. ----- 7. -----
3. Th о коллинеарн. векторах. Th о компланарн. веторах Th1. Система двух не нулевых векторов Д-во: 1. Необход.
β 2. Дост-ть. ----- Th2. Система 3-х векторов ЛЗ тттк вектора компланарны. Th3. Система 4-х векторов всегда ЛЗ. 4. Th о разлож. вектора по некомпланарн. векторам. Коорд. вектора. Ортонормир. базис. Базисом в пр-ве назыв. 3 некомпл. вектора, взятых в опред. порядке. Базисом на плоск. назыв. 2 неколлин. вектора на этой плоск., взятых в опред. порядке. Базисом на прямой назыв. люб. ненулев. вектор этой прямой. Th. Кажд. вектор м. б. разложен по базису в пр-ве и это разложение единств. Пусть
Системой коорд. в пр-ве назыв. совокупность базиса Вектор Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Два вектора называются ортогональными, если угол между ними равен прямому углу.
Скалярн. произв-е векторов. Применение скалярн. произв-я Углом м-у векторами Скалярн. произв-ем двух векторов назыв. число, равное произв-ю длин этих векторов на cos угла м-у ними/
Замечание: Если 1 из векторов нулевой, Св-ва
3 4. если Приложение скалярного произведения 1. ( 2. 3. связь с проекциями
4. Необх. и дост. услов. перп-сти двух ненулев. векторов явл. рав-во 0 их скалярн. произв-я
6. Векторное произв-е (опр-е, вычисл-е, св-ва) Упорядоч. тройка некомпл. векторов Сист. корд. назыв. правой, если её базисные векторы образ. правую тройку. При переест. местами двух соседних векторов ориентация тройки меняется. Если тройка При круговой переест. векторов ориентация тройки не меняется. Векторн. произв-ем вектора 1. | 2. Тройка векторов 3. Вектор Замечание: | Св-ва: 1. [ 2. [λ 3. 4. Th 1. Необх. и дост. услов. коллин-ти двух векторов явл. рав-во Д-во: ----- Th 2. Если 2 вектора | Д-во:
+
Следствие: Если 2 вектора 7. Смешанное произв-е (опр-е, вычисл-е, св-ва) Если вектор Тh. Смеш. произв-е некомпл. векторов Д-во:
Следствие 1: [
Следствие 2 (критерий компланарности 3-х векторов): Необх. и дост-ным услов. компланарности 3-х векторов явл. рав-во 0 их смеш. произв-я.
Th. Е сли 3 вектора Д-во:
= Следствие:
Ориентация плоскости
Парал. перенос Перенесём нач. корд. из т. О в т. О’ парал. переносом осей Пусть в старой сист. корд. XOY т.М(x,y) в новой т. М(x’,y’). Сист. корд. Связь координат т. М(x,y) и М(x’,y’) в старой и новой системе:
Ур-е кривых 2-го порядка, когда их центры симметрии наход-ся в т. O’(x0,y0), получ. с пом. преобраз. корд при парал. переносе осей. (x-x0)2+(y-y0)2=R2 – ур-е окружности в т. (x0,y0) радиусом R (x-x0)2/а2 (y-y0)2=2p(x-x0) – ур-е параболы с вершиной в т. (x0,y0) (x-x0=-- Поворот осей координат
Угол м-у двумя прямыми L1: y=k1x+b1, L2: y=k2x+b2
Если прямые зад. общими ур-ми: L1: A1x+B1y+C1=0, L2: A2x+B2y+C2=0
Эллипс Эллипсом назыв. геом. место точек M(x;y), для кот. сумма расстояний до 2-х зад. т. F1(c;0),F2(-с;0), назыв. фокусами эллипса, постоянна и равна 2а. По опр-ю | | Восп-ся форм-ми расст. м-у 2-мя т: | r1+r2=2a
т.к a>c,
x2/a2 + y2/b2 =1 - канонич. ур-е эллипса Эл-ты эллипса: О – центр эллипса, ABCD – вершины эллипса F1(c;0), F2(-с;0) - фокусы эллипса 2с - фокусное расстояние, кот. вычисл. по ф-ле с=
AC=2a, BD=2b - большая и малая полуоси эллипса Ɛ=с/a (Ɛ <1) - эксцентриситет эллипса, Ɛ = Эксцентриситет опр-ся отношением осей эллипса и характериз.т его форму. Прямые, парал. малой оси и отстоящие от нее на расстояние a/Ɛ, назыв. директрисами эллипса. Ур-е директрисы: X=±a/ Ɛ; a/ Ɛ >a т.е Ɛ <1 Фокальный параметр P= Окружность предст. собой геом. место точек, равноудал. от т. О, назыв. центром окружн-ти, a=b=п
Гипербола Гиперболой назыв. геом. место точек M(x;y), для кот. абсол. величина разности расстояний до 2-х зад. т. F1(c;0),F2(-с;0), назыв. фокусами гиперболы, постоянна и равна 2а (a<c) По опр-ю | Найдем:| |r1-r2|=2a; r1-r2=±2a
X2/a2 - y2/b2 =1 - канонич. ур-е гиперболы Эл-ты гиперболы: О – центр гиперболы, A,B – вершины гиперболы F1(c;0),F2(-с;0) – фокусы гиперболы 2с - фокусное расстояние, кот. вычисл. по ф-ле AB=2a – действит.. ось гиперболы. СD=2b – мнимая ось гиперболы Ɛ=с/a - эксцентриситет гиперболы, Ɛ = Эксцентритет опр-ся отношением осей гиперболы и характеризует ее форму: чем больше эксцентриситет, тем более вытянут вдоль мнимой оси основной прямоуг-к гиперболы. Ур-я директрис имеют вид: х=±a/Ɛ; т.к Ɛ >1 то a/Ɛ <a Асимптоты гиперболы – это прямые, к кот. ветви гиперболы неограниченно приближаются при удалении на бесконечность k=±tgα=±b/a y=kx=± Фокальный параметр P=
Парабола Параболой назыв. геом. место точек M(x;y), равноудаленных от зад. т. F( Канонич. ур-е параболы м.б. получ. из опр-я: F(
Эл-ты параболы: О- вершина параболы ОХ – ось параболы F( х= - p – фокальный параметр (расстояние от фокуса до директрисы или половина хорды, проходящ. ч-з фокус перпенд. оси ОХ)
Эллипсоид Будем вращать эллипс x2/a2 + y2/b2 =1 вокруг OУ. Согл. ф-ле (F(±
Обобщая, получ. При a=b=c=R получ. ур-е сферы x2+y2+z2=R2 Если рассек. эллипсоид плоскостями, перпенд. осям коорд, то все ее сечения будут эллипсами
Понятие вектора и лин. опер. над вект-ми. Св-ва опер. слож. вект-ов и умнож. вект-а на число (с док-вом)
Величины, для опр-я кот. дост-но знать одно число, назыв. скаляром. Геом. вектором назыв. направл. отрезок (характ-ся длиной (модулем) и направл-ем). Своб. векторы счит. равным и, если модули равны и направл. одинак. Вектора не явл. своб., если сущ. т. приложения вектора или линия действия вектора (связанные и скользящие.) Длиной вектора назыв. расстояние от нач. к концу вектора. Нулевым вектором назыв. вектор, у кот. начало и конец совпад. Векторы назыв. коллинеарными, если лежат на одной прямой, либо на парал. прямых. Нулевой вектор коллинеарен люб. вектору. 3 вектора назыв. компланарными, если они лежат в одной плоск., либо в парал. плоск-ях. Если тройка векторов содерж. нулевой вектор или пару коллинеарн. векторов, то эти векторы комплан. Два вектора равны, если они коллинеарны, имеют одинак. длину и направл-е. Линейные операции 1. Суммой векторов Св-ва: 1. 2. ( 3. (Ǝ 4. Правило парал-ма: Если Вычитание 1 сп. 2 сп. 3. Произведение Св-ва: 1. k*( 2. 3. λ*(β* 4. 1*
1. Д-ва: 1. ABCD – парал-м, ( 2.
3. Д-во вытек. из опр-й суммы векторов и нулевого вектора.
|
||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 170; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.234.230 (0.217 с.) |



 и
и  назыв. вектор
назыв. вектор  , идущ. из нач. вектора
, идущ. из нач. вектора 

 )(ᵾ
)(ᵾ  +
+  )
)
 -
-  =
=  ,
, на действ. число kϵR есть вектор k*
на действ. число kϵR есть вектор k*  коллин. к вектору
коллин. к вектору  +
+  , kϵR
, kϵR *λ +
*λ +  =
=  ,
, 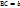 ,
,  +
+  =
=  =
=  =
=  =
= 



 как вектор, коллин. вектору
как вектор, коллин. вектору 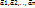 ϵV назыв. вектор
ϵV назыв. вектор  вида
вида  +λ2*
+λ2*  +..+λn*
+..+λn*  , где λ1,λ2,..,λn ϵ R
, где λ1,λ2,..,λn ϵ R в. п. V назыв. ЛЗ если найд. такие скаляры λ1,λ2,..,λn, из кот. хотя бы 1 отлично от нуля, что линейн. комбинация векторов
в. п. V назыв. ЛЗ если найд. такие скаляры λ1,λ2,..,λn, из кот. хотя бы 1 отлично от нуля, что линейн. комбинация векторов 
 λ1*
λ1*  +λ2*
+λ2*  +..+λn*
+..+λn*  =
= 
 только при услов. что λ1=λ2=…=λn=0
только при услов. что λ1=λ2=…=λn=0 , то она ЛЗ.
, то она ЛЗ. ЛЗ т.т.т.к. векторы коллинеарны.
ЛЗ т.т.т.к. векторы коллинеарны. =
=  *
*  некомпланарные
некомпланарные  = λ
= λ 

 , идущ. из нач. корд. в т. М назыв. радиус-вектором т. М. Координатами т. М (α,β,γ) назыв. корд. вектора
, идущ. из нач. корд. в т. М назыв. радиус-вектором т. М. Координатами т. М (α,β,γ) назыв. корд. вектора  и
и 
 , назыв. наименьш. угол, на кот. надо повернуть вектор
, назыв. наименьш. угол, на кот. надо повернуть вектор  до совмещ. с вектором
до совмещ. с вектором 

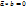
 (
( )
) (λ
(λ  λ
λ  *(
*( )=(
)=( )
) то (
то ( )>0 и (
)>0 и (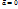
 )=
)=  =|
=|  |*cos(
|*cos( )=|
)=|  *cos0=
*cos0= 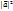 =>
=>  =
=  =
= 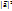 =>|
=>|  =
= 

 =|
=|  ,
,  )=
)= 
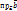 =|
=| 
 ((
((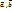 )=90) ó
)=90) ó  кратчайш. поворот 1-го вектора
кратчайш. поворот 1-го вектора  – правая, то
– правая, то  – левая
– левая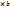 если вып. услов.
если вып. услов.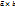 |=
|=  *sin(
*sin( явл. правой
явл. правой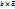 ]
] =
=  +
+ 
 =
=  ó
ó 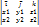
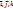 - правая
- правая


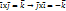
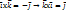


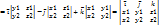
 скалярно умнож. на
скалярно умнож. на  .
. 
 ,
, 

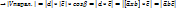
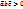 , если
, если 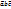 – прав.
– прав. , если
, если  =[
=[ 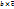 ]*
]*  *
*  , аоск. тройки векторов
, аоск. тройки векторов 
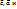
 ,
,  имеют одинак. ориентацию (циклич. перестан. знака не меняет). Не циклич. перестан. в смеш. произв. привод.
имеют одинак. ориентацию (циклич. перестан. знака не меняет). Не циклич. перестан. в смеш. произв. привод.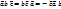
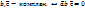
 =
= 

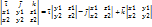
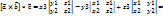

 получ. из сит. корд. XOY парал. переносом осей, при кот. нач. корд. O’(x0,y0) в XOY.
получ. из сит. корд. XOY парал. переносом осей, при кот. нач. корд. O’(x0,y0) в XOY.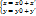 ó
ó 
 (y-y0)2/b2 =1– ур-е эллипса, гиперболы с центром симметрии в т. (x0,y0) (
(y-y0)2/b2 =1– ур-е эллипса, гиперболы с центром симметрии в т. (x0,y0) (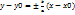 - ур-е асимптот)
- ур-е асимптот) – ур-е директрисы)
– ур-е директрисы)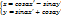 - ф-ла выраж. старые корд. ч-з новые этой же т. при повороте осей на угол
- ф-ла выраж. старые корд. ч-з новые этой же т. при повороте осей на угол 

 =>
=> 
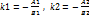

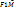 |+|
|+|  |=2a,
|=2a,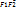 |=2c, a>c
|=2c, a>c =
=  ; |
; |  =
= 

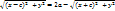


 :возводим в квадрат и группируем
:возводим в квадрат и группируем





 .
. - это половина хорды, провед. ч-з фокус, параллельно малой оси.
- это половина хорды, провед. ч-з фокус, параллельно малой оси. – ур-е окружн. с центром (x0,y0) и радиусом r.
– ур-е окружн. с центром (x0,y0) и радиусом r.  – канонич. ур-е окружн.
– канонич. ур-е окружн. |=2a, |
|=2a, |  |=
|= 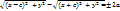



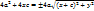


 *(-1)
*(-1)
 , т.к. по услов. C>a
, т.к. по услов. C>a


 *x – ур-я асимптоты
*x – ур-я асимптоты
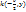 , M(x,y), FM=MK,
, M(x,y), FM=MK, 

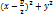 =
= 
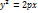
 ;y)=0) получим след. ур-е поверхн.
;y)=0) получим след. ур-е поверхн. – эллипсоид вращ-я, a,b –полуоси эллипсоида вращения.
– эллипсоид вращ-я, a,b –полуоси эллипсоида вращения. - ур-е эллипсоида, где все полуоси a,b,c-разные.
- ур-е эллипсоида, где все полуоси a,b,c-разные.


