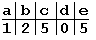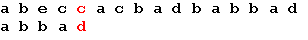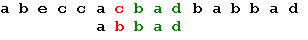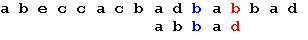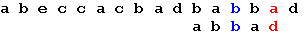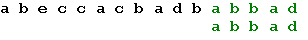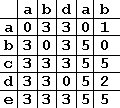Современные вычислительные машины. 4 принципа фон неймана. Создание виртуальной машины на Jscript.

Введение.

Данный текст предназначен для несчастных людей, не сдавших скрипты с первого раза, в том числе и меня. Написав электронный вариант ответов на все 10 вопросов, я предполагал (по договоренности с преподавателем) получить зачёт. Но меня обломали. Теперь буду сдавать его устно. Поскольку я писал текст «к которому не должно было возникнуть вопросов», он довольно сложный, но стоит поразбирать его дольше 10и минут, и любой желающий сможет его понять. Формулировки вопросов предоставлены Домуховским, Баклановский даёт их несколько короче, поэтому в ответах содержится куча дополнительной информации, которую сказать на зачёте будет вовсе нелишним. Ответы – это куча склеенной и обработанной информации из и-нета и лекций, к сожалению нам не читали на лекции тему «Конечные автоматы», так что её вам придётся искать самостоятельно. Удачи.

 

На данный момент, готовясь по этому мануалу, зачёт сдали несколько человек, различным преподавателям. Так что смотрите сами, я сдал зачёт Баклановскому J.

 

Мальчик В Кепке J

Кн-104, 2006г.

Современные вычислительные машины. 4 принципа фон Неймана. Создание виртуальной машины на Jscript.

В основу построения подавляющего большинства ЭВМ положены принципы, сформулированные в 1945 году американским ученым венгерского происхождения ДЖОНОМ фон НЕЙМАНОМ. Он описал, как должен быть устроен компьютер, чтобы он был универсальным и эффективным устройством для обработки информации.

Принципы:

• Двоичная система счисления:

Фон Нейман убедительно продемонстрировали преимущества двоичной системы для технической реализации – использование технических элементов с двумя возможными состояниями, например: есть ток - нет тока, намагничен - не намагничен. Так же он продемонстрировал удобство и простоту выполнения в ней арифметических и логических операций. ЭВМ стали обрабатывать и нечисловые виды информации - текстовую, графическую, звуковую и другие, но двоичное кодирование данных по-прежнему составляет информационную основу любого современного компьютера и занимает 90% времени работы.

• Организация памяти вычислительной машины:

Память компьютера представляется, как упорядоченная последовательность мест для хранения единиц информации. Такие места называются ячейками памяти. Для того чтобы сохранять информацию в этих ячейках, а также получать к ней доступ, компьютер должен уметь идентифицировать каждую из ячеек. В силу этого, каждая ячейка памяти имеет уникальный адрес, определяющий местоположение этой ячейки в памяти. При этом необходимо помнить, что большинство компьютеров располагают миллионами отдельных ячеек памяти, каждая из которых имеет собственный адрес. Информацию, содержащуюся в ячейке памяти, называют содержимым ячейки. Каждая ячейка памяти всегда имеет какое-либо содержимое.

Информацию, содержащуюся в единственной ячейке памяти, в действительности можно разделить на более мелкие составляющие, известные как байты. Байт — это объем памяти, необходимый для содержания единственного символа. Число байтов в одной ячейке памяти может варьироваться. А байт, в свою очередь, состоит из более мелких единиц информации, известных как биты. Термином бит (bit), который является производной от слов binary digit (двоичная цифра), обозначается мельчайший элемент информации, которой способен манипулировать компьютер. Бит может принимать два значения 0 или 1. Как правило, байт состоит из восьми битов.

Каждое значение в памяти представлено определенным набором нулей и единиц. Компьютер может либо заносить значение в память, либо осуществлять его выборку из памяти. При занесении значения в память компьютер устанавливает каждый бит соответствующей ячейки в 0 или в 1, уничтожая при этом предыдущее содержимое ячейки. При выборке значения из памяти компьютер копирует набор нулей и единиц, содержащийся в этой ячейке, для обработки; при этом содержимое ячейки сохраняется.

• Однородная память:

Первоначально программа задавалась путем установки перемычек на специальной коммутационной панели. Это было весьма трудоемким занятием. Нейман первым догадался, что программа может также храниться в виде нулей и единиц, причем в той же самой памяти, что и обрабатываемые ею числа. Отсутствие принципиальной разницы между программой и данными дало возможность ЭВМ самой формировать для себя программу в соответствии с результатами вычислений. Программы и данные хранятся в одной и той же памяти. Поэтому ЭВМ не различает, что хранится в данной ячейке памяти - число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.

• Работа процессора:

Программа, хранящаяся в памяти, состоит из набора команд (инструкций), которые выполняются процессором автоматически друг за другом в определенной последовательности. У процессорадва основных предназначения: координирование всех операций компьютера и выполнение арифметических и логических операций над введенными данными. Руководствуясь инструкциями, содержащимися в компьютерной программе, процессор решает, какие операции ему следует выполнить и в каком порядке. А затем он передает компонентам компьютера управляющие сигналы для координирования их совместной работы. Например, если инструкция предписывает осуществить считывание элемента данных, процессор посылает необходимые управляющие сигналы на устройство ввода.

При выполнении программы, содержащейся в памяти, процессор последовательно считывает каждую инструкцию этой программы, определяет, что эта инструкция предписывает сделать, и осуществляет выборку данных, необходимых для выполнения данной инструкции. А далее процессор приступает к реальной обработке этих данных. Результаты этой обработки также помещаются в память. Процессор способен выполнять такие арифметические операции, как сложение, вычитание, умножение и деление. Также, процессор способен сравнивать содержимое двух ячеек, а затем, в соответствии с результатами этого сравнения, принимать определенное решение.

Принципы организации ЭВМ фон Неймана стали общепринятыми по двум причинам: ведущие разработчики Вычислительной Техники того времени уже использовали их в той или иной мере, и авторитет автора придал им определенную академичность. Сам же вопрос приоритета все таки остаётся спорным.

 

Создание виртуальной машины на Jscript сводится к созданию:

1. Системы ввода-вывода, которая позволит пользователю данной программы вводить определённые данные на обработку и потом видеть результат этой обработки. Чтение данных можно организовать из файла или по средствам их чтения из командной строки. Вывод данных может осуществляться либо на экран, либо в файл.
2. Памяти, куда будет складываться введённые данные и результаты их обработки. Работа с памятью подразумевает возможность в любое время обратиться к хранящимся в ней данным.
3. Процессора, который должен уметь обрабатывать имеющиеся в памяти данные в соответствии с вводимыми командами.

 

Алгоритм Хаффмана.

Хаффмановское кодирование появилось в 1952 году. Главное его предназначение заключалось в упаковке текстовых файлов - для другого он мало приспособлен. Имеет довольно простую реализацию, так что его вполне удобно использовать в устройствах имеющих слабые микропроцессоры.

Алгоритм основан на том факте, что некоторые символы из стандартного 256-символьного набора в произвольном тексте могут встречаться чаще среднего периода повтора, а другие, соответственно, – реже. Следовательно, если для записи распространенных символов использовать короткие последовательности бит, длиной меньше 8, а для записи редких символов – длинные, то суммарный объем файла уменьшится.

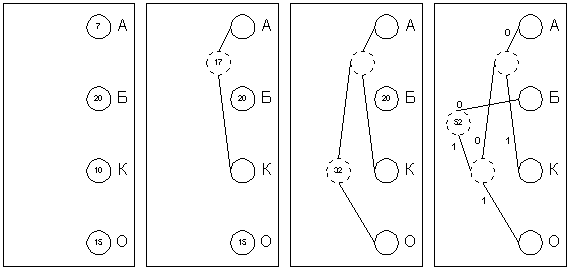
Хаффман предложил очень простой алгоритм определения того, какой символ необходимо кодировать каким кодом для получения файла с длиной, очень близкой к его энтропии. Пусть у нас имеется список всех символов, встречающихся в исходном тексте, причем известно количество появлений каждого символа в нем. Выпишем их вертикально в ряд в виде ячеек будущего графа по правому краю листа. Выберем два символа с наименьшим количеством повторений в тексте (если три или большее число символов имеют одинаковые значения, выбираем любые два из них). Проведем от них линии влево к новой вершине графа и запишем в нее значение, равное сумме частот повторения каждого из объединяемых символов. Отныне не будем принимать во внимание при поиске наименьших частот повторения два объединенных узла (для этого сотрем числа в этих двух вершинах), но будем рассматривать новую вершину как полноценную ячейку с частотой появления, равной сумме частот появления двух соединившихся вершин. Будем повторять операцию объединения вершин до тех пор, пока не придем к одной вершине с числом. Для проверки: очевидно, что в ней будет записана длина кодируемого файла. Теперь расставим на двух ребрах графа, исходящих из каждой вершины, биты 0 и 1 произвольно – например, на каждом верхнем ребре 0, а на каждом нижнем – 1. Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до нее, выписывая нули и единицы по маршруту следования. Для рисунка символ "А" получает код "000", символ "Б" – код "01", символ "К" – код "001", а символ "О" – код "1".

 

В теории кодирования информации показывается, что код Хаффмана является префиксным, то есть код никакого символа не является началом кода какого-либо другого символа. Проверьте это на нашем примере. А из этого следует, что код Хаффмана однозначно восстановим получателем, даже если не сообщается длина кода каждого переданного символа. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации. Например, при приеме "0100010100001" им сначала отделяется первый символ "Б": "01-00010100001", затем, снова начиная с вершины дерева – "А" "01-000-10100001", затем аналогично декодируется вся запись "01-000-1-01-000-01" "БАОБАБ".

Классический алгоритм Хаффмана имеет один недостаток: для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот появления символов, которая должна высылаться впереди данных.

Код Хэмминга.

Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Контроль целостности данных осуществляется путём добавления к данным определённого количества контрольных бит, которое зависит от размера передаваемых данных. Количество необходимых контрольных бит можно определить из следующего неравенства:

d + p + 1 ≤ 2 ^p,

где d - размер блока данных в битах, p - количество необходимых контрольных бит. Обычно для характеристики кода Хэмминга используют пару (c, d), где с - длина передавемого блока данных с контрольными битами, а d - чистая длина данных. Например, (11, 7) означает, что передаваемая длина данных - 7 бит, количество контрольных бит равно 4, что составляет общую длину блока 11 бит. В отличае от других методов коррекции ошибки, где контрольные биты дописываются в конец или начало блока данных (либо вообще в другом пакете данных), биты кода Хэмминга записываются вместе с данными в строго определённых позициях. Здесь и делее мы будем нумеровать биты не с нуля, а с единицы. Тогда позиции в которых записываются контрольные биты соответствуют степеням двойки (2^k, k = 0, 1, 2,...), то есть 1, 2, 4, 8 и т.д.
Рассмотрим механизм работы кода Хэмминга на примере передачи 7-битового кода 1110011. Для контроля целостности блока данных такой длины, нам необходимо 4 бита кода Хэмминга, которые записываются в позициях 1, 2, 4, 8:

Позиция бита                       Значение бита       *       *   * * Таблица 1 - Расположение битов кода Хэмминга (отмечены '*')

Контрольная сумма формируется путем выполнения операции "исключающее ИЛИ" над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3.

сумма   Таблица 2 - Нахождение контрольной суммы

Полученная контрольная сумма записывается в соответствующие разряды блока данных - младший бит в младший разряд. Таким образом формируется следующий блок данных:

Позиция бита                       Значение бита                       Таблица 3 - Результирующий блок данных

Просуммировав коды позиций с ненулевыми битами получаем 0, что является признаком корректного блока данных.

сумма   Таблица 4 - Проверка корректности блока данных

Теперь рассмотрим два случая ошибки: 1) ошибка в бите 7 - бит 0 заменён на бит 1 и 2) ошибка в бите 5 - бит 1 заменён на бит 0. Просуммируем коды позиций с ненулевыми битами:

сумма     сумма   Таблица 5 - Контрольная сумма в блоках данных содержащих ошибку

В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме.

Поиск подстроки в строке. Постановка задачи, решение методом «грубой силы». Возможность оптимизации. Понятие хэш-функции, сравнительные характеристики хэш-функций. Поиск подстроки в строке при помощи хэш-функций.

Задача поиска подстроки в строке заключается в нахождении в оригинальной строке, точного вхождения (соответствие всех символов) подстроки. В результате программа должна выдать номера символов всех вхождений подстроки…

Метод Грубой силы.

Этот алгоритм заключается в проверке всех позиций текста с 0 по n – m (n-длина строки, m-длина подстроки) на предмет совпадения с началом образца. Если совпадает - смотрим следующую букву и т.д.

Алгоритм грубой силы не нуждается в предварительной обработке и дополнительном пространстве.

Оптимизацией метода грубой силы является алгоритм хэш функции…

Хэш-функции

Хэш-функция - это преобразование, получающее из данных произвольной длины некое значение фиксированной длины. Простейшими примерами являются контрольные суммы. Бывают криптографические и программистские хэши. Криптографический хэш отличается от программистского следующими двумя свойствами: необратимостью и свободностью от коллизий. Обозначим m - исходные данные, h(m) - хэш от них. Необратимость означает, что если известно число h0, то трудно подобрать m такое, что h(m) = h0. Свободность от коллизий означает, что трудно подобрать такие m1 и m2, что m1!= m2, но h(m1) = h(m2).
Криптографические хэш-функции разделяются на два класса:
- хэш-функции без ключа
- хэш-функции с ключом.

Хэш-функции без ключа разделяются на два подкласса:
- слабые хэш-функции,
- сильные хэш-функции.
Слабой хэш-функцией называется односторонняя функция H(x), удовлетворяющая следующим условиям:
1) аргумент х может быть строкой бит произвольной длины;
2) значение H(x) должно быть строкой бит фиксированной длины;
3) значение H(x) легко вычислить;
4) для любого фиксированного x вычислительно невозможно найти другой x'!= x, такой что H(x')=H(x).
Пара x'!= x, когда H(x')=H(x) называется коллизией хэш-функции. Сильной хэш-функцией называется односторонняя функция H(x), удовлетворяющая условиям 1-3 для слабой хэш-функции и свойству 4':
4') вычислительно невозможно найти любую пару x'!= x, такой что H(x')=H(x).
Поскольку из свойств 1-2 следует, что множество определения хэш-функции значительно шире множества значений, то коллизии должны существовать. Свойство 4 требует, чтобы найти их для заданного значения х было практически невозможно. Требование 4' говорит о том, что у сильной хэш-функции вычислительно невозможно вообще найти какую-либо коллизию.

Хэш-функцией с ключом называется функция H(k,x) удовлетворяющая свойствами:
1) аргумент х функции H(k,x) может быть строкой бит произвольной длины;
2) значение H(k,x) должно быть строкой бит фиксированной длины;
3) при любых k и x легко вычислить H(k,x);
4) для любого х должно быть трудно вычислить H(k,x) не зная k;
5) должно быть трудно определить k даже при большом числе неизвестных пар {x, H(k,x)} при выбранном наборе х или вычислить по этой информации H(k,x') для x'!= x.

Многие криптографические преобразования (в частности, вычисление и проверка электронной цифровой подписи, ЭЦП) выполняются над данными фиксированного размера. Поэтому перед простановкой электронной подписи под многобегабайтным файлом обычно рассчитывают значение хэш-функции от него, а уже от этого значения считают ЭЦП. Кроме того, удобно, например, пароли в базе хранить не в открытом виде, а в хэшированном.

Вот некоторые алгоритмы хэш-функций:
MD2
Автор: FIXME!
Размер: 128 бит.

MD4
Автор: Р.Райвест (R. Rivest).
Размер: 128 бит.

MD5. Капитально переделанный MD4.
Автор: Р.Райвест (R. Rivest).
Размер: 128 бит.

SHA.
Один из (относительно) новых алгоритмов свертки.
Автор: FIXME!
Размер: 160 бит.

ГОСТ Р34.11-94
Российский алгоритм. Размерность получаемого значения очень удобна для формирования по паролю ключа для ГОСТ 28147-89.
Автор: FIXME!
Размер: 256 бит.

Рассмотрим поиск подстроки в строке с помощью хэш-функции. Каждый символ имеет свой уникальный код от 0 до 255. Суть метода заключается в том, чтобы для подстроки подсчитать некоторую хэш-функцию (например, сумму кодов всех символов в строке), затем посчитать ту же самую хэш-функцию для части строки, равной по длине подстроке, и, в случае совпадения хэш-функции, полностью сравнить его. Ускорение работы алгоритма связано с тем, что мы каждый раз не пересчитываем каждый раз хэш-функцию, а только отнимаем значение функции от самого "старого" символа и добавляем значение функции от следующего символа.

Метод Грубой силы.

Этот алгоритм заключается в проверке всех позиций текста с 0 по n – m (n-длина строки, m-длина подстроки) на предмет совпадения с началом образца. Если совпадает - смотрим следующую букву и т.д.

Алгоритм грубой силы не нуждается в предварительной обработке и дополнительном пространстве.

Оптимизацией метода грубой силы является алгоритм Боэра-Мура…

Алгоритм Боэра-Мура

Алгоритм Боэра-Мура, разработанный двумя учеными – Боэром (Robert S. Boyer) и Муром (J. Strother Moore), считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска подстроки в строке. Прежде чем рассмотреть работу этого алгоритма, уточним некоторые термины. Под строкой мы будем понимать всю последовательность символов текста. Собственно говоря, речь не обязательно должна идти именно о тексте. В общем случае строка – это любая последовательность байтов. Поиск подстроки в строке осуществляется по заданному образцу, т. е. некоторой последовательности байтов, длина которой не превышает длину строки. Наша задача заключается в том, чтобы определить, содержит ли строка заданный образец.

Простейший вариант алгоритма Боэра-Мура состоит из следующих шагов. На первом шаге мы строим таблицу смещений для искомого образца. Процесс построения таблицы будет описан ниже. Далее мы совмещаем начало строки и образца и начинаем проверку с последнего символа образца. Если последний символ образца и соответствующий ему при наложении символ строки не совпадают, образец сдвигается относительно строки на величину, полученную из таблицы смещений, и снова проводится сравнение, начиная с последнего символа образца. Если же символы совпадают, производится сравнение предпоследнего символа образца и т. д. Если все символы образца совпали с наложенными символами строки, значит мы нашли подстроку и поиск окончен. Если же какой-то (не последний) символ образца не совпадает с соответствующим символом строки, мы сдвигаем образец на один символ вправо и снова начинаем проверку с последнего символа. Весь алгоритм выполняется до тех пор, пока либо не будет найдено вхождение искомого образца, либо не будет достигнут конец строки.

Величина сдвига в случае несовпадения последнего символа вычисляется исходя из следующих соображений: сдвиг образца должен быть минимальным, таким, чтобы не пропустить вхождение образца в строке. Если данный символ строки встречается в образце, мы смещаем образец таким образом, чтобы символ строки совпал с самым правым вхождением этого символа в образце. Если же образец вообще не содержит этого символа, мы сдвигаем образец на величину, равную его длине, так что первый символ образца накладывается на следующий за проверявшимся символ строки.

Величина смещения для каждого символа образца зависит только от порядка символов в образце, поэтому смещения удобно вычислить заранее и хранить в виде одномерного массива, где каждому символу алфавита соответствует смещение относительно последнего символа образца. Поясним все вышесказанное на простом примере. Пусть у нас есть набор символов из пяти символов: a, b, c, d, e и мы хотим найти вхождение образца “abbad” в строке “abeccacbadbabbad”. Следующие схемы иллюстрируют все этапы выполнения алгоритма:

 

Таблица смещений для образца “abbad”.

 

Начало поиска. Последний символ образца не совпадает с наложенным символом строки. Сдвигаем образец вправо на 5 позиций:

 

Три символа образца совпали, а четвертый – нет. Сдвигаем образец вправо на одну позицию:

 

Последний символ снова не совпадает с символом строки. В соответствии с таблицей смещений сдвигаем образец на 2 позиции:

 

Еще раз сдвигаем образец на 2 позиции:

 

Теперь, в соответствии с таблицей, сдвигаем образец на одну позицию, и получаем искомое вхождение образца:

 

Хотя рассмотренный упрощенный алгоритм вполне пригоден с практической точки зрения (и часто применяется), нельзя не заметить, что результаты сравнений используются недостаточно эффективно. Действительно, на втором шаге, когда у нас совпали три символа, мы, зная, что последовательность “bad” встречается в образце только один раз, могли бы сразу сместить образец на всю его длину, а не на один символ. Теперь мы рассмотрим другой, немного более сложный вариант алгоритма Боэра-Мура, позволяющий учесть результаты предыдущих сравнений в случае частичного совпадения образца и подстроки. Прежде всего изменим принцип построения таблицы смещений. В этом варианте алгоритма таблица – двумерная, каждому символу образца соответствует один столбец таблицы, а каждой букве алфавита – одна строка. В ячейках таблицы содержатся значения смещений, на которые нужно сдвинуть образец, если при проверке данного символа образца обнаружено несовпадение и вместо искомого символа получен символ алфавита, соответствующий некоторой строке в таблице. Например, таблица последовательности “abdab” для нашего пятибуквенного алфавита будет выглядеть следующим образом:

 

Заполнение таблицы начинается с последнего столбца. Самый правый столбец таблицы фактически соответствует массиву, который используется в упрощенном варианте алгоритма. Следующие столбцы содержат значения сдвига для образца при условии, что предыдущие (при движении справа налево) символы совпали. Проводя поиск при помощи этой таблицы, мы последовательно просматриваем значения ячеек, лежащих на пересечении столбца, соответствующего символу образца и строки, соответствующей символу текста. Просмотр начинается с последнего столбца. Если в каждом столбце выбранная ячейка содержит 0, значит, подстрока найдена. Если значение ячейки отличается от нуля, мы сдвигаем образец на соответствующее значение.

Определенные сложности могут возникнуть при работе с кодировкой Unicode. Очевидно, что таблица, число строк которой равно числу символов двухбайтовой кодировки, будет слишком громоздкой. К счастью, в такой таблице нет необходимости, ведь в случае двухбайтовой кодировки любой образец содержит лишь небольшую часть символов алфавита. Для всех символов, не содержащихся в образце, значения смещения в каждом столбце таблицы будут одинаковыми. Эта особенность позволяет разработать сокращенные варианты таблицы для Unicode. Unicode-строку можно рассматривать как последовательность байтов, где каждый Unicode-символ представлен двумя байтами.

Дополнительным преимуществом данного варианта алгоритма является возможность организовать «регистронезависимый» поиск, т. е. поиск слова вне зависимости от регистра букв. Для этого достаточно в таблице смещений сопоставить одинаковые строки одним и тем же буквам разного регистра. Можно даже ввести поиск по шаблону, содержащему подстановочные символы.

Превосходство алгоритма Боэра-Мура перед методом грубой силы наиболее ощутимо проявляется с увеличением длины образца. Хотя алгоритм Боэра-Мура производит меньше сравнений, чем примитивный алгоритм при длине образца более двух символов, большая сложность этого алгоритма и необходимость заранее вычислять таблицу смещений может свести на нет его преимущества, если поиск проводится в коротком тексте, и длина образца невелика.

Преимущество в быстродействии более сложного варианта алгоритма Боэра-Мура перед более простым вариантом сказывается, только если длина образца велика, и в тексте часто встречаются отдельные последовательности символов, содержащиеся в образце. Главное же достоинство более сложного варианта алгоритма заключается в возможности реализации регистронезависимого поиска и поиска по шаблону.

Разбор арифметических выражений. Понятие дерева выражений, понятие префиксной, инфиксной и суффиксной записи. Алгоритм Дэйкстры перевода строки из инфиксной формы в суффиксную форму. Вычисление значения выражения, записанного в суффиксной форме.

Понятие выражения

Под «выражением» или «математическим выражением» подразумевается строка, в которой есть операнды и действия. Каждый операнд состоит ровно из одного символа, причем этот символ не может быть таким же, как символ одного из действий. В выражении используются четыре типа операции: +, -, *, /. Первыми выполняются операции умножения и деления. Все операции являются бинарными операторами (т.е. они работают с двумя операндами).

Типы записи выражений

Каждое математическое выражение можно представить в трех специфических видах записи:

Префиксная запись — сначала пишется действие, затем левый операнд, затем правый операнд. Для выражения (a+b) префиксная запись будет иметь вид +ab. Выражению (a+b*(c+d)) соответствует запись +a*b+cd (складываем a с произведением b и суммы c и d)

Инфиксная запись выражения — пишется левый операнд, затем пишется знак действия и правый операнд. Инфиксная запись отличается от других тем, что в не соблюден порядок действий. Ее очень легко получить из выражения, просто убрав скобки: (a+b*(c+d)) соответствует a+b*c+d

Постфиксная запись выражения — пишется левый операнд, затем пишется правый операнд и знак операции. Для выражения (a+b) постфиксная запись имеет вид ab+. Выражению (a+b*(c+d)) соответствует запись abcd+*+. Её можно прочитать с конца, аналогично префиксной записи.

Эти типы записи были введены польским логиком Яном Лукасевичем, поэтому их также называют системой польского обозначения. С помощью постфиксной (инфиксной) записи легко вычисляется значение выражения.

Определение дерева

Некоторая вершина типа T (корень) с конечным числом связанных с ней отдельных деревьев с типом узлов T, называемых поддеревьями.

Из определения дерева ясно, что линейный список можно рассматривать как дерево, в котором каждая вершина имеет не более одного поддерева. Поэтому список иногда назы-вают вырожденным деревом.

Будем считать, что дерево состоит из узлов, которые имеют указатели на своего предка, и правого и левого потомков. Потомки в свою очередь тоже являются узлами. Узел, не имеющий потомков, назовем листом дерева. Дерево определятся узлом, которое будем называть корневым. Корневой узел может в определенных условиях меняться. В качестве информационной части у узла будет переменная символьного типа.

Под деревом выражения будет называть дерево, которое можно построить из математического выражения. Каждый узел (не лист) такого дерева содержит знак действия, а каждый лист один из индетификаторов выражения. Дерево строится так, чтобы по нему можно было восстановить порядок действий.

Например, пусть задано простое арифметическое выражение вида:

(A+B)*(C+D)-E

Представим это выражение в виде дерева, в котором узлам соответствуют операции, а ветвям - операнды. Построение начнем с корня, в качестве которого выбирается операция, выполняющаяся последней. Левой ветви соответствует левый операнд операции, а правой ветви - правый. Дерево выражения показано ниже:

- / \ / \ * E / \ / \ / \ / \ + + / \ / \ / \ / \ A B C D

Совершим обход дерева, под которым будем понимать формирование строки символов из символов узлов и ветвей дерева. Обход будем совершать от самой левой ветви вправо и узел переписывать в выходную строку только после рассмотрения всех его ветвей. Результат обхода дерева имеет вид:

AB+CD+*E- (1)

Это постфиксная/суффиксная запись выражения или обратная польская запись.

Обратная польская запись обладает рядом замечательных свойств, которые превращают ее в идеальный промежуточный язык при трансляции. Во-первых, вычисление выражения, записанного в обратной польской записи, может проводиться путем однократного просмотра, что является весьма удобным при генерации объектного кода программ. например, вычисление выражения (1) может быть проведено следующим образом:

|-----|----------------------|-----------------------|| # | Анализируемая | Действие || п/п | строка | ||-----|----------------------|-----------------------|| 0 | A B + C D + * E - | r1=A+B || 1 | r1 C D + * E - | r2=C+D || 2 | r1 r2 * E - | r1=r1*r2 || 3 | r1 E - | r1=r1-E || 4 | r1 | Вычисление окончено ||-----|----------------------|-----------------------|Здесь r1, r2 - вспомогательные переменные. Для того чтобы, имея дерево выражения, записать его в префиксной форме нужно читать его по следующему правилу: узел, левый операнд, правый.

Для инфиксной записи: левый операнд, узел, правый.

Получение обратной польской записи из исходного выражения может осуществляться так же весьма просто на основе простого алгоритма, предложенного Дейкстpой. Для этого вводится понятие стекового приоритета операций:

|----------|-----------|| Операция | Приоритет ||----------|-----------|| (| 0 ||) | 1 || +|- | 2 || *|/ | 3 || ** | 4 ||----------|-----------|

Просматривается исходная строка символов слева направо, операнды переписываются в выходную строку, а знаки операций заносятся в стек на основе следующих соображений:

а) если стек пуст, то операция из входной строки переписывается в стек;???

б) операция выталкивает из стека все операции с большим или равным приоритетом в выходную строку;

в) если очередной символ из исходной строки есть открывающая скобка, то он проталкивается в стек;

г) закрывающая круглая скобка выталкивает все операции из стека до ближайшей открывающей скобки, сами скобки в выходную строку не переписываются, а уничтожают друг друга.

Процесс получения обратной польской записи выражения схематично представлен в следующей таблице:

Просматриваемый символ

Входная строка

(

A

+

B

)

*

(

C

+

D

)

-

E

Состояние стека

(

(

+ (

+ (

*

(*

(*

+ (*

+ (*

*

-

-

Выходная строка

A

B

+

C

D

+

*

E

-

Введение.

Данный текст предназначен для несчастных людей, не сдавших скрипты с первого раза, в том числе и меня. Написав электронный вариант ответов на все 10 вопросов, я предполагал (по договоренности с преподавателем) получить зачёт. Но меня обломали. Теперь буду сдавать его устно. Поскольку я писал текст «к которому не должно было возникнуть вопросов», он довольно сложный, но стоит поразбирать его дольше 10и минут, и любой желающий сможет его понять. Формулировки вопросов предоставлены Домуховским, Баклановский даёт их несколько короче, поэтому в ответах содержится куча дополнительной информации, которую сказать на зачёте будет вовсе нелишним. Ответы – это куча склеенной и обработанной информации из и-нета и лекций, к сожалению нам не читали на лекции тему «Конечные автоматы», так что её вам придётся искать самостоятельно. Удачи.

 

На данный момент, готовясь по этому мануалу, зачёт сдали несколько человек, различным преподавателям. Так что смотрите сами, я сдал зачёт Баклановскому J.

 

Мальчик В Кепке J

Кн-104, 2006г.

Современные вычислительные машины. 4 принципа фон Неймана. Создание виртуальной машины на Jscript.

В основу построения подавляющего большинства ЭВМ положены принципы, сформулированные в 1945 году американским ученым венгерского происхождения ДЖОНОМ фон НЕЙМАНОМ. Он описал, как должен быть устроен компьютер, чтобы он был универсальным и эффективным устройством для обработки информации.

Принципы:

• Двоичная система счисления:

Фон Нейман убедительно продемонстрировали преимущества двоичной системы для технической реализации – использование технических элементов с двумя возможными состояниями, например: есть ток - нет тока, намагничен - не намагничен. Так же он продемонстрировал удобство и простоту выполнения в ней арифметических и логических операций. ЭВМ стали обрабатывать и нечисловые виды информации - текстовую, графическую, звуковую и другие, но двоичное кодирование данных по-прежнему составляет информационную основу любого современного компьютера и занимает 90% времени работы.