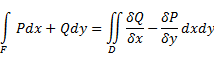Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу
Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу Пусть z=f(x,y) – непрерывно дифференцируемая и положительная функция двух переменных, определенная на ограниченном подмножестве (S) плоскости Пусть дано некоторое тело (V) в трехмерном пространстве Свойства Теорема 1: справедливо равенство Теорема 2: пусть функции f(x,y) и ϕ(x,y) определены на одном и том же множестве (S) плоскости
Теорема 3: пусть функция f(x,y) определена на квадратируемом подмножестве (S) плоскости
Теорема 4: пусть f(x,y) Теорема 5: справедлива формула Теорема 6: (теорема о среднем) пусть функция двух переменных z=f(x,y) определена и интегрируема на замкнутом множетсве (S)с
Теорема 7: всякая непрерывная в области (S) функция z=f(x,y) интегрируема. Теорема 8: если функция z=f(x,y) ограничена и имеет разрывы только лишь на конечном числе гладких кривых области (S), то она интегрируема. Приведение двойного интеграла к повторному Пусть функция двух переменных z=f(x,y) определена на прямоугольнике Теорема: пусть для функции существует двойной интеграл
Замена переменных, якобиан. Полярные цилиндрические, сферические координаты: дифференциал площади, объема. Пусть функция z=f(x,y) определена на области с кусочно-гладкой границей. Рассмотрим двойной интеграл Теперь произведем произвольную замену переменных: x=ϕ(ξ,η), y=ψ(ξ,η). J(ξ,η)= Общая формула замены переменных:
Полярные координаты X=rcosϕ,y=rsinϕ. Якобиан = r. Тогда: Сферические координаты X=rcosθcosϕ, y=rcosθsinϕ, z=rsinθ. Якобиан = dS=rdrdϕ, dV= Кривая, дифференциал ее длины, интеграл по длине кривой. Кривая описывается выражением: (x,y,z) 4. Поверхность, дифференциал ее площади, интеграл по площади поверхности. Пусть (S) – поверхность в пространстве, заданная явным уравнением z=f(x,y). Тогда площадь поверхности (S), заданное явным уравнением вычисляется по формуле
Пусть теперь поверхность (S) задана параметрическими уравнениями x=x(u,v), y=y(u,v), x=x(u,v) или то же самое, векторным уравнением dS= Работа плоского поля: формула Грина как частный случай теоремы Остроградского-Гаусса. Пусть P(x,y) и Q(x,y) гладкие в области D, а Г – контур в области D, ограниченный под областью D. Тогда:
Формула Грина является частным случаем теоремы Остроградского-Гаусса, когда поверхность является плоской. Кратные интегралы: определение, условия существования, основные свойства. Сведение к повторному интегралу Пусть z=f(x,y) – непрерывно дифференцируемая и положительная функция двух переменных, определенная на ограниченном подмножестве (S) плоскости
Пусть дано некоторое тело (V) в трехмерном пространстве Свойства Теорема 1: справедливо равенство Теорема 2: пусть функции f(x,y) и ϕ(x,y) определены на одном и том же множестве (S) плоскости
Теорема 3: пусть функция f(x,y) определена на квадратируемом подмножестве (S) плоскости
Теорема 4: пусть f(x,y) Теорема 5: справедлива формула Теорема 6: (теорема о среднем) пусть функция двух переменных z=f(x,y) определена и интегрируема на замкнутом множетсве (S)с
Теорема 7: всякая непрерывная в области (S) функция z=f(x,y) интегрируема. Теорема 8: если функция z=f(x,y) ограничена и имеет разрывы только лишь на конечном числе гладких кривых области (S), то она интегрируема. Приведение двойного интеграла к повторному Пусть функция двух переменных z=f(x,y) определена на прямоугольнике Теорема: пусть для функции существует двойной интеграл
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.168.16 (0.015 с.) |
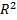 . Если существует предел
. Если существует предел  независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается
независимо от выбора точек и независимо от разбиения множества (S) на элементарные части, то он называется двойным интегралом функции и обозначается  .
.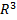 . Предположим, что известна плотность
. Предположим, что известна плотность 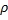 (x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел
(x,y,z) распределения массы в каждой точке M(x,y,z) тела (V). Требуется определить всю массу тела. Если существует предел 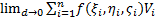 независимо от выбора точек (
независимо от выбора точек (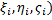 и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
и независимо от разбиения множества (V) на элементарные части, то он называется тройным интегралом функции f(x,y,z) по множеству (V).
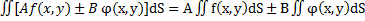 , где А и В постоянные числа.
, где А и В постоянные числа.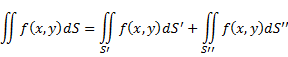
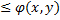 для всех (x,y)
для всех (x,y) 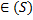 и существуют двойные интегралы функции f(x,y) и
и существуют двойные интегралы функции f(x,y) и 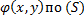 . Тогда справедливо равенство
. Тогда справедливо равенство 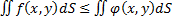
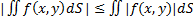
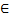 (S), что
(S), что
 , т.е. на множестве точек (x,y)
, т.е. на множестве точек (x,y)  , которые удовлетворяют условию
, которые удовлетворяют условию 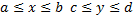 где a<b, c<d
где a<b, c<d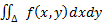 и также при каждом фиксированном x
и также при каждом фиксированном x 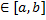 существует обычный интеграл I=
существует обычный интеграл I= 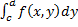 . Тогда существует повторный интеграл
. Тогда существует повторный интеграл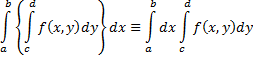
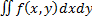 и в нем произведем замену переменных x=aξ+bη, y=cξ+bη, где J=
и в нем произведем замену переменных x=aξ+bη, y=cξ+bη, где J= 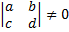 . Тогда
. Тогда  .
.
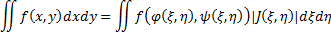
 .
.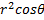 . Тогда, при переходе к сферическим координатам подынтегральная функция умножится на
. Тогда, при переходе к сферическим координатам подынтегральная функция умножится на  .
. , x=x(t), y=y(t), z=z(t), t
, x=x(t), y=y(t), z=z(t), t  . Если кривая задана уравнениями ρ=ρ(ϕ), ϕ
. Если кривая задана уравнениями ρ=ρ(ϕ), ϕ  .
.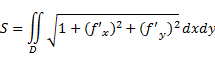
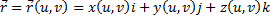 . Тогда площадь поверхности вычисляется по формуле
. Тогда площадь поверхности вычисляется по формуле 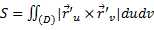 . Или
. Или  , где E=
, где E= 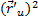 , F=
, F=  , G=
, G= 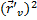 .
.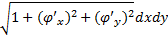 , поверхностный интеграл первого рода равен
, поверхностный интеграл первого рода равен  .
.