
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
До лабораторних робіт з інженерної геодезіїСтр 1 из 4Следующая ⇒
для студентів денної та заочної форм навчання Напряму підготовки Будівництво, освітньо-кваліфікаційного рівня „бакалавр” Полтава 2011 Методичні вказівки. Частина І до лабораторних робіт з інженерної геодезії для студентів денної та заочної форм навчання напряму підготовки 6.060101 – будівництво, освітньо-кваліфікаційного рівня „бакалавр”. – Полтава: ПолтНТУ, 2011. – 30 с.
Укладачі: І.Ю. Богдан, П.С. Корба – кандидати фіз.-мат. наук, доценти.
Відповідальний за випуск: В.Й. Хазін, завідувач кафедри проектування автомобільних доріг і сільських будівель, к.т.н., професор.
Рецензент: О.С. Сергеєв, ст. викл. кафедри проектування автомобільних доріг і сільських будівель.
Затверджено на засіданні науково-методичної ради університету Протокол № 1 від 29 березня 2011 р. Коректор М.М. Рокитна Верстка Т.М. Ільченко ЗАГАЛЬНІ ЗАУВАЖЕННЯ Методичні вказівки до лабораторних робіт складені відповідно до програми курсу інженерної геодезії і мають на меті закріплення теоретичних положень дисципліни, вироблення практичних навичок роботи з геодезичними приладами та обробки результатів геодезичних вимірів. При виконанні лабораторних робіт необхідно дотримуватися правил техніки безпеки й правил поводження з геодезичними приладами. До лабораторних робіт допускаються підготовлені студенти; готовність перевіряє викладач за відповідями на контрольні питання. Вихідні дані для виконання лабораторних робіт наводяться в методичних вказівках або видаються викладачем. Звіт про виконання роботи – заповнений журнал лабораторної роботи, який подається викладачу в кінці заняття. Не виконані вчасно лабораторні роботи студент відпрацьовує самостійно у визначений викладачем час.
ПРАВИЛА ПОВОДЖЕННЯ З ГЕОДЕЗИЧНИМИ ПРИЛАДАМИ – Переносити прилад слід у вертикальному положенні, держачи його за підставку й уникаючи струсів та ударів. Перенесення приладу, закріпленого на штативі, допускається тільки на невеликі відстані при майже вертикальному його положенні. – Нормальне робоче положення приладу – на штативі. При встановленні приладу на штатив необхідно поставити його так, щоб він став посередині головки штатива, й, держачи рукою, закріпити становим гвинтом. Ні в якому разі не залишати прилад на штативі не закріпленим. На місцевості башмаки ніжок штатива повинні бути вдавлені в землю, а в лабораторії знаходитись у спеціальних заглибленнях на підлозі.
– Перш ніж приступати до роботи геодезичним приладом, треба перевірити, чи підіймальні та навідні гвинти знаходяться в середині їх ходу, при необхідності встановити їх в потрібне положення. Забороняється працювати ними, коли вони стоять у крайньому положенні, й ні в якому разі не крутити їх силою після того, як вони дійшли до упору. – При роботі з приладами рухомі його частини слід переміщати так, щоб їх рух здійснювався плавно, без поштовхів і щоб для цього не потрібно було докладати зайвих зусиль, тобто все має рухатись від одного дотику до нього. – Підіймальні гвинти приладу повинні крутитись вільно, тому, щоб запобігти їх передчасному зношуванню, необхідно: а) слідкувати, щоб головка штатива була якомога горизонтальнішою, що виключає їх зайве обертання при приведенні приладу в робоче положення; б) крутити їх тільки при неповністю закріпленому становому гвинті, який остаточно затискається тільки після горизонтування приладу. – Усі закріплювальні гвинти приладу повинні бути затиснені невеликим зусиллям, а їх послаблення необхідно робити тільки на півобороту.
1. масштаби топографічних планів і карт Мета – навчитись розв´язувати задачі на масштаб й знаходити його точність, будувати й використовувати графічні масштаби. Завдання для підготовки до роботи Вивчити [1, с. 29-33; 2, с. 20-24]. Знати, що називається масштабом топоплану й карти та що означає знаменник числового масштабу. Вміти розрізняти великий (крупний) масштаб від дрібного та швидко визначати горизонтальне прокладення лінії на місцевості в метрах, що відповідає відрізку на плані величиною 1 см і 1 мм. Розуміти, що таке точність масштабу і з якою точністю записувати довжину лінії на місцевості, визначену за допомогою карти. Навчитись будувати й користуватись простим лінійним та поперечним масштабами. Контрольні питання
1. Що таке масштаб топоплану чи карти, які бувають масштаби та для чого потрібен масштаб? 2. На що вказує знаменник числового масштабу? 3. Що називають основою графічного масштабу? 4. Яке призначення нахилених ліній сітки поперечного масштабу? 5. Що приймають за граничну графічну точність і що називають точністю масштабу?
Приладдя та інструменти: лінійка поперечного масштабу, циркуль-вимірювач, олівець.
Порядок виконання роботи Завдання 1.1. Обчислити довжину лінії D1 на місцевості, якщо на плані масштабу 1: N1 вона зображується відрізком d1. Знайти точність масштабу й отриманий результат D1 записати з цією точністю. Приклад. Вихідні дані: 1: N1 = 1:1000; d1 = 7,50 см (вибираються згідно зі своїм номером у списку групи з табл. 1.1). При розв´язуванні цієї задачі складають пропорцію: 1 см на плані масштабу 1:1000 відповідає 10 м, а відрізку 7,50 см буде відповідати лінія D1, звідки
Оскільки точність масштабу t – це довжина лінії на місцевості, якій на плані відповідає 0,1 мм, то склавши аналогічну пропорцію
і запис отриманого результату потрібно зробити до десятих часток метра, тобто D1 = 75,0 м. Таблиця 1.1 Вихідні дані для розв´язування завдань 1.1 – 1.4
Завдання 1.2. Знайти відрізок d2, яким зображується на плані масштабу 1: N2 виміряна на місцевості лінія, горизонтальне прокладення якої має величину D2, результат записати з граничною графічною точністю, тобто до 0,01 см. Приклад. Вихідні дані: 1: N2 = 1:500; D2 = 26,10 м (із табл. 1.1). Цю задачу розв´язують, склавши таку ж пропорцію, як і в завданні 1.1, звідки
Слід зауважити, що подібні задачі можна розв´язувати, помноживши або поділивши довжину лінії на плані чи місцевості на знаменник масштабу, тобто для завдання 1.1 D1 = d1 × N1 =7,50 см × 1000 = 7500 см = 75,0 м, а для завдання 1.2 d2 =
Завдання 1.3. Побудувати для числового масштабу 1: N1 простий лінійний масштаб з основою а, позначити на ньому довжину лінії D1. Приклад. Вихідні дані: 1: N1 = 1:1000 (із табл. 1.1). Із табл. 1.1 вибирають основу масштабу а (наприклад 2,0 см). На горизонтальній прямій відкладають 4 – 6 основ, рівних вибраній основі а, і першу основу зліва ділять на 10 частин. Оскільки в масштабі 1: 1000 1 см на плані відповідає відрізок 10 м на місцевості, то на масштабі це буде величина 20 м, а мала поділка першої основи дорівнює 2 м, тобто 0,1 а. На розміченій прямій ставлять нуль в кінці першої основи і цифрами, кратними 20 м, оцифровують основи, відкладені справа від нуля, а зліва від нуля малі поділки оцифровують через 2 м, як на рис. 1.1.
Рис. 1.1. Лінійний масштаб
На лінійному масштабі будь-яка довжина лінії дорівнює сумі цілого числа основ справа від нуля (на рис. 1.1 – 60 м) і частини першої основи, яка відраховується за допомогою малих поділок зліва від нуля (15 м). Точність лінійного масштабу складає приблизно 0,2 його малої поділки, тобто для нашого прикладу – 0,4 м.
Завдання 1.4. Для заданого масштабу 1: N2 побудувати поперечний масштаб, у якого основа а, число поділок по горизонталі зліва від нуля n = 10 і по вертикалі m = 10. Позначити на ньому довжину лінії D2 . Приклад. Вихідні дані: 1: N2 = 1:500; а = 2,0 см; n = m = 10; D2 = 25,25 м Поперечний масштаб точніший від простого лінійного, оскільки в ньому для відрахування частки малої поділки зліва від нуля використовується принцип пропорційного поділу відрізка. Для його побудови на горизонтальній прямій відкладаємо 4 – 6 відрізків, рівних заданій основі а, і в кінці першої основи, як і в лінійному масштабі, ставимо нуль. Із намічених точок проводимо перпендикуляри і на крайніх із них наколюємо 10 рівних довільних за величиною відрізків, кінці яких з´єднуємо горизонтальними лініями. Першу нижню й верхню основи зліва від нуля ділимо на 10 частин і через отримані точки проводимо косі лінії (трансверсалі), з´єднуючи нуль на нижній основі із першою точкою зліва від нуля верхньої основи, потім першу точку нижньої основи з другою точкою верхньої основи і так далі, поки не побудуємо сітку поперечного масштабу, як на рис. 1.2.
Рис. 1.2. Поперечний масштаб
Оцифровку нижньої горизонтальної лінії поперечного масштабу проводять точно так, як і лінійного масштабу. Щоб оцифрувати поперечний масштаб по вертикалі, обчислюють у метрах величину його найменшої поділки, яку називають точністю поперечного масштабу Сітку поперечного масштабу зазвичай наносять канавками на спеціальних металевих пластинках, які називаються масштабними лінійками. Якщо циркулем-вимірювачем одну ніжку (праву) вести по вертикальній лінії масштабної лінійки, а другу (ліву) по косій лінії (трансверсалі), то переміщення циркуля на одну поділку вверх буде відповідати зміні довжини лінії на величину найменшої поділки масштабу.
Побудований поперечний масштаб для нашого прикладу зображений на рис. 1.2. Відкладена на ньому довжина D2 = 25,25 м є сумою великого відрізка, що дорівнює цілому числу основ справа від нуля (20 м), меншого відрізка, рівного цілому числу малих поділок зліва від нуля (5 м) і найменшого відрізка між вертикальною та косою лініями (0,25 м), який відраховується по вертикальній оцифровці масштабу.
2. Визначення на топографічній карті довжини лінії, плоских прямокутних координат точки Мета – навчитись визначати на топографічній карті довжини ліній, плоскі прямокутні координати точки та орієнтирні кути напрямків. Завдання для підготовки до роботи Вивчити [1, с. 19-22, 24-26; 2, с.20-24, 25,27-31]. Мати уявлення про систему плоских прямокутних координат, що застосовується при побудові топопланів, розуміти, що означають координати х, у і як їх визначити на топопланах і картах. Знати, як на топокартах показують взаємне положення основних напрямків, що використовуються при орієнтуванні ліній, тобто географічного, магнітного й осьового меридіанів, як враховувати знаки зближення меридіанів g і схилення магнітної стрілки d та які орієнтирні кути вимірюють на топокарті, а які обчислюють і в якому порядку. Контрольні питання 1. З якою точністю можна визначити на топоплані чи карті довжини ліній? 2. Як розміщується на топокарті сітка прямокутних координат і що означають координати х, у якоїсь точки? 3. Що називається планом і картою? 4. Який із орієнтирних кутів вимірюється на топокарті? 5. В якому порядку визначають на топокарті орієнтирні кути? 6. Де на топокарті приводяться значення схилення магнітної стрілки та зближення меридіанів? Матеріали й приладдя: топографічна карта з нанесеною лінією АВ, масштабна лінійка, транспортир, циркуль-вимірювач, олівець.
Порядок виконання роботи Завдання 2.1. Виміряти на топокарті горизонтальне прокладення лінії АВ. У відповідності з масштабом своєї карти оцифровують поперечний масштаб (карту й масштабну лінійку одержують на кафедрі). Узятий із карти розхилом циркуля-вимірювача відрізок лінії прикладають до лінійки поперечного масштабу й по його оцифровці відраховують її горизонтальне прокладення (як на рис. 1.2). Якщо масштабної лінійки немає, то лінію на карті вимірюють до 0,1 мм звичайною лінійкою з міліметровими поділками й отриманий результат перемножують на знаменник масштабу карти. Остаточний результат записують в метрах з точністю масштабу карти.
Завдання 2.2. Визначити на топокарті плоскі прямокутні координати вказаної точки, номер зони, в якій знаходиться дана точка, та її відстань від осьового меридіана зони.
На топокарті нанесена координатна сітка, лінії якої підписані в кілометрах на її рамці. Щоб не мати справи з від´ємними значеннями ординат, початок координат, тобто точка перетину осьового меридіана зони з екватором, зміщена на 500 км на захід. Для однозначного визначення положення точки на поверхні землі перед ординатою в оцифровці вертикальних ліній кілометрової сітки вказують номер зони. Щоб визначити на карті координати х і у якої-небудь точки, необхідно до координат хС і уС, знятих з рамки для найближчих до цієї точки ліній кілометрової сітки, алгебраїчно додати виміряні за допомогою циркуля-вимірювача і масштабної лінійки прирости координат Dх і Dу, тобто відстані точки від цих ліній сітки
Для точки А на рис. 2.1 значення хА = 6611000 м + 295 м = 6611295 м; уА = 97650000 м – 301 м = 9764699 м. Згідно з цими координатами точка А знаходиться в дев´ятій зоні на схід від осьового меридіана на відстані у¢А = 764699 м – 500000 = 264699 м.

Рис. 2.1. Визначення координат х і у точки Завдання 2.3. Виміряти дирекційний кут aАВ лінії АВ, обчислити її географічний азимут (Аг)АВ, магнітний азимут (Ам)АВ, осьовий румб rАВ і зворотний дирекційний кут aВА. На карті через точку А паралельно вертикальним лініям координатної сітки олівцем проводять допоміжну лінію, тобто лінію, паралельну осьовому меридіану зони. Транспортиром вимірюють із максимальною точністю дирекційний кут aАВ від північного напрямку проведеної лінії до лінії АВ. Географічний азимут (Аг)АВ і магнітний азимут (Ам)АВ обчислюють послідовно за формулами:
Значення зближення меридіанів g і схилення магнітної стрілки d, що входять у формули (2.2), виписують з карти, де вони даються на схемі взаємного розміщення меридіанів в легенді під західною частиною рамки. При цьому значенням g і d, які записані на схід від географічного меридіана, позначеного зіркою, приписують знак „плюс”, а західним − знак „мінус”. Для обчислення осьового румба rАВ використовують виміряний дирекційний кут aАВ і формули залежності між дирекційними кутами і румбами (табл. 2.1).
Таблиця 2.1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.161.132 (0.048 с.) |
 .
.
 = 5,22 см.
= 5,22 см.
 = 0,0522 м = 5,22 см.
= 0,0522 м = 5,22 см.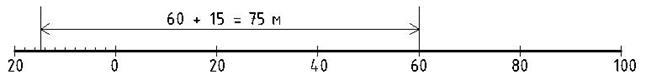

 і яка при n = m =10 складає
і яка при n = m =10 складає  основи а. Числами, кратними величині найменшої поділки, й оцифровують поперечний масштаб по вертикалі від нуля (внизу) до величини малої поділки (вверху). Ці числа дорівнюють горизонтальним відрізкам між перпендикуляром до основи та косою лінією, що виходять з нульової точки. Таким чином, коса лінія слугує для того, щоб за її допомогою знімати частини малих поділок, що зліва від нуля, точно, а не на око, як це має місце в лінійному масштабі.
основи а. Числами, кратними величині найменшої поділки, й оцифровують поперечний масштаб по вертикалі від нуля (внизу) до величини малої поділки (вверху). Ці числа дорівнюють горизонтальним відрізкам між перпендикуляром до основи та косою лінією, що виходять з нульової точки. Таким чином, коса лінія слугує для того, щоб за її допомогою знімати частини малих поділок, що зліва від нуля, точно, а не на око, як це має місце в лінійному масштабі.



