
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема дедукції (з доведенням).Стр 1 из 2Следующая ⇒
Теорема дедукції (з доведенням). Если Г – множество формул и А, В – формулы, и из Г и А выводима В (Г,А|-В), то из Г|-А->B. Доказательство: Г,А|-В согласно определению, существует последовательность формул В1,В2… Вn, Вn=В. Мы должны показать, что Г|-А->Bk. Мат. Индукция: I) k=1; Г|-А->B1; B1=B; B1: 1) аксиома, 2) одна из формул Г, 3) Формула А. В1 – выводимая по определению вывода. 1) А->(B->A) //aкс I-1 2) B1->(A->B1) // SA B B1 A 3) MP: A->B1-выводима Следов., Г |-A->B1 II) Г |-A->Bi (i<k) III) Г |-A->Bk -? Bk: 1)аксиома, 2) одна из формул Г, 3) Формула А,4)получена из формулы Bi Bj (i,j<k)
1) Bi -> (Bi->Bk) 2) Г |-A->Bi 3) Г |-A->(Bi->Bk) 4) (A->(B->C))->((A->B)->(A->C))// aкс I-2 5) (A->(Bi->Bk))->((A->Bi)->(A->Bk)) // S… 6) (A->Bi)->(A->Bk) //MP 3,5 7) A->Bk //MP 2,6
k=n; Г|-A->Bn или Г |-A->B
Теорема дедукции связывает между собой формальное доказательство и выводимость из гипотезы. Она дает возможность переходить от выводимости из гипотез к теореме, которые свободны от гипотез. Визначення інтерпретації. Формальне визначення істинності. Интерпрета́ция: совокупность значений (смыслов), придаваемых тем или иным способом элементам (выражениям, формулам, символам. Задать интерпретацию первой сигнатуры 1. Некоторое непустое множество М, называемое носителем интерпретации или универсумом. 2. С каждой константой с, 3. Каждому к-местному функциональному символу 4. Каждому к-местному предикатному символу Адгебра – множество с заданными на нем операциями(функциями). Модель – множество с заданными на нем отношениями(предикатами). Алгебраическая система – множество, с отношениями и операциями. Формула A называется истинной в данной интерпретации I тогда и только тогда, когда она выполнена на всякой последовательности из ∑.
Ложной – если не выполнена ни на одной последовательности из ∑.
Властивості числення предикатів першого порядку (розвязність, повнота, несуперечність) Главными из свойств являются полнота (для любой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). Теорема Чёрча. Исчисление предикатов неразрешимо.
Теорема Гёделя о полноте ИП в широком смысле.
Исчисление предикатов первого порядка – полная теория. Во всяком ИП первого порядка теоремами являются все те и только те формулы, которые логически общезначимы. Исчисление предикатов первого порядка – не противоречивая теория. Исчисления называется полным в узком смысле, если присоединение к его аксиомама какой нибудь не выводимой в нем формулы приводит к противоречию. ИП первого порядка является неполным в узком смысле.
Алгоритм уніфікації. Процесс подстановок с целью получения подходящих резолюций дизъюнктов называется унификацией.
Под композицией 2 подстановок a, b: a *b (ab) называется результат применения подстановки b к результату подстановки a с последующей подстановкой тех пар из b, в которых имеется переменная,не вошедшая в a и выбрасыванием тех пар из b, в которых имеется переменная, вошедшая в a Множество литералов {Li} называется унифицированным, если существует такая подстановка q:
Подстановка q называется унификатором. Наиболее общим простейшим унификатором для множества литералов Li является подстановка qp такая, что для любого другого унификатора выполняется: Множеством рассогласования для множества литералов называется множество термов, отличающихся в первой позиции слева. Алгоритм унификации (для 2 литералов): Lk- множество литералов, Dk- множество рассогласования, qk- подстановка на k-ом шаге. Начальный этап: L0, q0. k-й этап: Если (k+1)-й этап: делаем подстановку
Дослідження властивостей формальних аксиоматичних теорій. Непротиворечивость Теория, в которой множество теорем покрывает всё множество формул (все формулы являются теоремами, «истинными высказываниями»), называется противоречивой. В противном случае теория называется непротиворечивой. Выяснение противоречивости теории — одна из важнейших и иногда сложнейших задач формальной логики. После выяснения противоречивости теория, как правило, не имеет дальнейшего ни теоретического, ни практического применения.
Полнота Теория называется полной, если в ней для любой формулы Независимость аксиом Отдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима. Разрешимость Теория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс(алгоритм), позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет. T4(об огран.лин.) Пусть (n+1)арная функция g –ПРФ,тогда (n+1)арная функция f задаваемая операцией огран.линией f(x1,..xn,y)= Док-во:Рассмотрим Зафиксируем набор x1,x2...,xn,y Пусть
Теза Черча і його значення. Следующие и рассматриваемые ранее классы функций совпадают. 1.Класс ЧРФ 2.Класс ф-й,вычислимых по Тьюрингу 3..............по Маркову 4........класс МНР вычислимых Все рассмотренные формальные модели являются различными математическими уточнениями интуитивного понятия АВФ. Тезис Чёрча: класс част. выч. функций совпадает с классом частичных алгоритм. вычислимых функций. Т.Ч. является природонаучным фактом,который подтверждается следующими результатами. 1.Существенно-различные формальные уточнения понятия АВФ, предложенные различными авторами оказались эквивалентными, в смысле задания одного и того же класса функций. Переход от задания функции в одном формализме в задании в другом формализме является конструктивным. 2.Все известные до сих пор алгоритмы вычисления функций оказались ЧРФ. Никому не удалось придумать пример функции, которая была бы АВФ, но не была ЧРФ 3.Для каждого из этих формализмов все заданные в конкретном формализме функций - АВФ в интуитивном смысле. Принципы Т. Тезис Чёрча превращает интуитивные понятия алгоритм.вычислимых и разрешимых функций в объекты мат.исследований. Использование Т.Ч.как аксиомы позволяет во многих случаях заменить формально заданные алгоритмы на их не форм. описания.
Теорема дедукції (з доведенням). Если Г – множество формул и А, В – формулы, и из Г и А выводима В (Г,А|-В), то из Г|-А->B. Доказательство: Г,А|-В согласно определению, существует последовательность формул В1,В2… Вn, Вn=В. Мы должны показать, что Г|-А->Bk. Мат. Индукция: I) k=1; Г|-А->B1; B1=B; B1: 1) аксиома, 2) одна из формул Г, 3) Формула А. В1 – выводимая по определению вывода. 1) А->(B->A) //aкс I-1 2) B1->(A->B1) // SA B B1 A 3) MP: A->B1-выводима Следов., Г |-A->B1 II) Г |-A->Bi (i<k) III) Г |-A->Bk -? Bk: 1)аксиома, 2) одна из формул Г, 3) Формула А,4)получена из формулы Bi Bj (i,j<k)
1) Bi -> (Bi->Bk) 2) Г |-A->Bi 3) Г |-A->(Bi->Bk) 4) (A->(B->C))->((A->B)->(A->C))// aкс I-2 5) (A->(Bi->Bk))->((A->Bi)->(A->Bk)) // S… 6) (A->Bi)->(A->Bk) //MP 3,5 7) A->Bk //MP 2,6
k=n; Г|-A->Bn или Г |-A->B
Теорема дедукции связывает между собой формальное доказательство и выводимость из гипотезы. Она дает возможность переходить от выводимости из гипотез к теореме, которые свободны от гипотез.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.024 с.) |
 ,
,  значит задать:
значит задать: сопоставить элемент
сопоставить элемент 
 сопоставить к-местную функцию
сопоставить к-местную функцию 
 сопоставить к-местный предикат
сопоставить к-местный предикат 
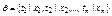 (переменную xi заменяем на терм ti)
(переменную xi заменяем на терм ti)

 .
. , то конец алгоритма, qk- наиболее общий унификатор. Если Dk содержит переменную xk и терм tk, и переменная xk входит в терм tk, то множество литералов не унифицируемо.
, то конец алгоритма, qk- наиболее общий унификатор. Если Dk содержит переменную xk и терм tk, и переменная xk входит в терм tk, то множество литералов не унифицируемо.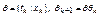

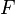 выводима либо сама
выводима либо сама 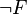 . В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.
. В противном случае, теория содержит недоказуемые утверждения (утверждения, которые нельзя ни доказать, ни опровергнуть средствами самой теории), и называется неполной.
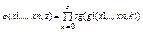
 ;
;  =
= 



