Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация и идентификация ⇐ ПредыдущаяСтр 7 из 7
В задачах медицинской диагностики, использующей новейшие методы построения диагностического правила, часто применяются и типовые решения. Положим, что имеется метод, обеспечивающий классификацию данных различной природы. Математические основы такой процедуры хорошо известны. Задача классификации, скажем нарушений в живом организме, и задача идентификации нарушений могут быть представлены как сопряженные математические процедуры. Если использовать термин “идентификация” в смысле построения поисковой процедуры, направленной на обнаружение заданного объекта — “нарушения”, “патологии”, личности, то нетрудно увидеть близость этих задач. В таком понимании процедура классификации может отождествляется с “верхним” уровнем, а идентификация — с “нижним”. Действительно, понимая процедуру идентификации как процесс отыскания объекта — личности, обладающей заданным типовым набором показателей состояния организма, мы решаем диагностическую задачу. Результатом такой процедуры является отнесение объекта всего к двум категориям: “норма” или “патология”. Или в терминах идентификационной процедуры личности: “свой” или “чужой”. Нормальное состояние индивидуального организма в терминах идентификационной процедуры означает “Свой”, а патология, с различными проявлениями, которые в последующем будут уточняться, может быть охарактеризована термином “Чужой”. Принимая во внимание эти понятия, рассмотрим типовую задачу. Положим, имеется некоторая выборка, полученная в процессе измерения величины физического параметра, регистрируемого с поверхности тела человека. В общем случае такая процедура носит название биометрии. Будем использовать основные элементы процедуры построения решающего правила для идентификации личности. Пусть имеется техническая система, посредством которой осуществляется измерение физического параметра. Будем считать, что система осуществляет измерение вектора v =(v 1, v 2,..., vk), состоящего из k существенно коррелированных биометрических параметров. Положим, что личность на этапе идентификации предъявила N своих динамических образов и, соответственно, мы имеем N реализаций векторов vi. Проанализировав имеющиеся реализации векторов биометрических параметров, мы можем найти характерный для личности интервал изменения каждого конкретного параметра [min(vj), max(vj)].
Если теперь при попадании параметра vj в интервал [min (vj), max(vj)] присваивать ej = 0, а при выпадении vj из интервала [min (vj), max(vj)] присваивать ej = 1, то мы получим вектор Хемминга. Для “Своего” этот вектор должен состоять практически из одних нулей. Для “Чужого”, предъявляющего иные биометрические параметры, вектор Хемминга будет иметь много несовпадений (много единиц). Для рассматриваемого случая биометрическим эталоном, зафиксированным при обучении, являются значения минимумов и максимумов измеряемых параметров. Тогда абсолютное значение расстояния Хемминга — Ex до биометрического эталона следует определить как общее число выпадений измерений за интервалы допустимых значений биометрического эталона. Расстояние Хемминга — Ex всегда положительно и может изменяться от 0 до k (где k — это число контролируемых биометрических параметров). Число примеров при обучении биометрической системы может существенно варьироваться. Как правило, биометрические системы, анализирующие динамические образы, опираясь на меру Хемминга, способны удовлетворительно работать при их обучении на 5...7 примерах, однако для их хорошей работы требуется порядка 20...30 примеров. Использование более 50...60 примеров для обучения системы перестает приносить ощутимые преимущества. Следует отметить, что задание в биометрическом эталоне интервалов допустимых значений измеряемых параметров может осуществляться различными способами. Используя понятия СКА, формирование интервалов, а точнее говоря, фрагментов, лучше проводить с использованием заранее определенного функционала, который регламентирует построение системы интервалов. На малых обучающих выборках целесообразно осуществлять прямое вычисление минимума и максимума измеренных значений контролируемых параметров. При объеме обучающей выборки в 5 и более примеров становится целесообразным вычисление математического ожидания значений параметров m (vj) и их дисперсий s (vj). В этом случае значение минимальной и максимальной границ принято вычислять следующим образом:
min(v j)= m (v j) - t(N,(1- P 1))Ч s(v j) max(v j)= m (v j) + t(N,(1- P 1))Ч s(v j) где N — число использованных при обучении примеров, P 1 — заданное значение вероятности ошибок первого рода (в этих операциях P 1 принимают равным 0,1), t (N,(1 – P 1)) — коэффициенты Стьюдента. При вычислении математического ожидания контролируемого параметра может использоваться формула:
Известно, что с ростом n оценка (3.3) приближается к точному значению математического ожидания в смысле Ляпунова и Чебышева. Основным недостатком (3.3) является то, что при обучении приходится помнить значения всех измеренных ранее параметров. Эта проблема усугубляется тем, что в неопределенном будущем может понадобиться дообучение биометрической системе и, следовательно, при использовании (3.3) приходится хранить все данных обучении неопределенно долго. Более удобным для реализации является рекуррентное вычисление математического ожидания:
При использовании (3.4) приходится помнить только общее число уже использованных примеров и текущее значение математического ожидания. На каждом последующем шаге появляется новое значение математического ожидания и запоминается i — число учтенных примеров. Аналогичная ситуация возникает и при вычислении дисперсии контролируемых параметров. Если хранятся все значения измеренных параметров, то может быть использована обычная форма вычисления:
При необходимости экономии памяти компьютера и времени вычислений используется рекуррентное вычисление дисперсии:
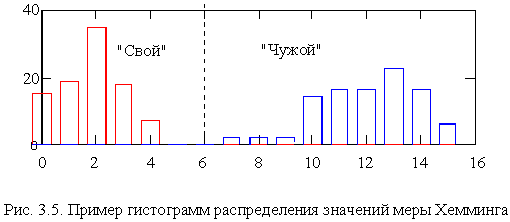
После того как сформирован биометрический эталон, возможна реализация процедур аутентификации зарегистрированного пользователя. При осуществлении процедур аутентификации “Свой” пользователь достаточно редко ошибается и, соответственно, мера Хемминга оказывается малой. Иначе обстоит дело при попытках аутентифицироваться “Чужих”. Для “Чужого” ошибки оказываются гораздо более частыми. Эта типовая ситуация иллюстрируется рис. 3.5, где приведен пример гистограмм “Свой” – “Чужой” биометрической системы контроля динамики регистрируемого сигнала.
Гистограмма получена для меры Хемминга, построенной на контроле 80 параметров. Из рис. 3.5 видно, что для “Своего” наиболее вероятным отклонением является значение Ex =2 и зафиксированное значение меры Хемминга не превосходит 5. Для “Чужого”, пытающегося подстроить динамику сигнала, мера Хемминга принимает значения от 7 и выше. В качестве разделяющего порога областей “Свой” “Чужой” может быть принято непопадание в заданные интервалы 6 контролируемых параметров. Отметим, что здесь понятие “интервала” очень близко совпадает по смыслу с понятием “фрагмент”, которое было рассмотрено в методе СКА. Этот пример соответствует хорошему разделению областей “Свой” и “Чужой” с достаточно примитивным решающим правилом. Для того чтобы задать порог, разделяющий эти области, необходимо вычислить значения математического ожидания меры Хемминга для области “Свой”, дисперсию для этой же области. Тогда можно воспользоваться следующими соотношениями: “Свой” если Ех < m (Ех Свой) +t (N,(1 –P 1))Ч s (Ех Свой), “ Чужой” если Ех > m (Ех Свой) + t (N,(1– P 1))Ч s (Ех Свой),
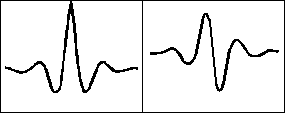
где t (N,(1– P 1)) — коэффициенты Стьюдента, N — число примеров при обучении, P 1 — заданная вероятность ошибки первого рода для системы в целом (обычно принимается P 1 =0,01). Полученные результаты позволяют увидеть хорошую взаимосвязь задач классификации и идентификации. Одновременно с этим отчетливо наблюдается связанность статистического и структурного координатного анализа. Следует подчеркнуть, что (3.7), (3.8) корректны только для закона распределения значений меры Хемминга, близкого к нормальному закону. Нормализация этого закона осуществляется при условии достаточно большого числа контролируемых параметров k >20 и выборе достаточно узких диапазонов допустимых значений параметров биометрического эталона. Вэйвлет-анализ Как мы теперь видим, распознавание различных нарушений в организме человека и опознание конкретного человека являются близкими задачами. И в том и другом случае приходится анализировать некоторые массивы данных. Развитие средств телекоммуникации позволяет по-новому взглянуть на решение этих проблем. Предоставляя доступ к информационным ресурсам большому числу абонентов, можно проводить массовые медицинские обследования населения и одновременно заботиться об идентификации абонентов, о конфиденциальности медицинской информации. И в том и другом случае можно строить диагностические алгоритмы – решения, используя типовые математические процедуры. При этом экспресс-диагностика в сети Интернет позволит значительно понизить требования к вычислительным ресурсам периферийных пользователей, не понижая качество диагностических заключений. Рассмотрим одно из перспективных направлений построения диагностических решений на основе так называемого Вэйвлет-анализа данных. Отметим, что использование этого метода впервые было апробировано в США в задаче идентификации личности по графическому образу — отпечатку пальца. Столкнувшись с необходимостью хранить отпечатки пальцев 30 млн человек по 600 килобайт на каждый палец или 6 мегабайт на запись, государство должно было потратить 200 млн долларов только на хранение информации. Сотрудники Лос-Аламосской лаборатории предложили использовать для сжатия отпечатков вэйвлет-преобразование. Вэйвлеты (wavelet) и вэйвлет-преобразование — это новый способ обработки и исследования сигналов, теория которого разработана совсем недавно, с появлением быстродействующих компьютеров, так как требует большого объема вычислений. Вэйвлет — это в дословном переводе “маленькая волна” (рис. 3.6). За основу обычно берется один из простейших графиков. Видно, что график быстро затухает по краям.
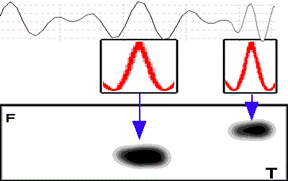
Рис. 3.6. Вэйвлет — “маленькая волна” Вэйвлет можно считать трехмерным спектром, где по оси X — время, по оси Y — частота, а по оси Z — амплитуда гармоники с данной частотой в данный момент времени (рис. 3.7).
Рис. 3.7. Результат Вэйвлет- анализа Обычно на двухмерной плоскости (на экране, на бумаге) ось Z отображают в виде градаций черного цвета. При этом черный цвет на графике характеризует максимальную, а белый — минимальную амплитуду сигнала. Тогда самые интересные места сразу видны по черным пятнам Далее этот вэйвлет прикладывается к сигналу (делается свертка), при этом его можно растягивать (т. е. менять частоту) и передвигать по временной оси (т. е. менять время). Мы получаем двухмерный массив амплитуд в зависимости от частоты и времени. Реально мы получаем комплексный массив (как и в спектре), но на рисунках изображены только амплитуды. Фазовая картинка выглядит очень красиво, но требует дополнительных пояснений. Существует алгоритм быстрого вэйвлет-преобразования, подобного Быстрому Преобразованию Фурье (БПФ) для спектров, время вычисления для которого значительно меньше. Также есть обратное вэйвлет-преобразование для восстановления формы сигнала. Вэйвлет-анализ разработан для решения задач, оказавшихся “очень сложными” для традиционного анализа Фурье, и находит все более широкое применение в исследовании и прогнозе временных рядов, например медицинской диагностики. Это может быть запись ЭКГ сигнала или рентгеновское изображение одного из органов. Вэйвлет-анализ применяется при обработке данных медицинского обследования, сжатии изображений и распознавании образов и речи, задачах связи, теоретической биофизике и математике. В простом изложении вэйвлет-анализ представляется обычной процедурой, понять которую несложно. Хорошо известно, что любой электрический сигнал можно разложить в сумму гармоник (синусоид) разной частоты. Но синусоидальное описание волны обеспечивается гладкими функциями, которые не очень-то отслеживают мельчайшие изменения сигнала во времени. Чтобы уловить эти изменения, вместо синусоидальных функций (волн) можно взять короткие “всплески” — совершенно одинаковые, но разнесенные по времени. Оказывается, этого недостаточно: надо добавить еще их всевозможные растянутые и сжатые копии. Вот теперь сигнал можно разложить в сумму таких всплесков разного размера и местоположения. Это и есть вэйвлет-анализ. По своему содержанию такой анализ имеет много общего с классическим Фурье анализом. Но он имеет явные отличия, которые выражаются в некоторой произвольной процедуре выбора “всплесков”. Однако если воспользоваться понятием фрагмента, которое используется в СКА, то “всплески” можно выбирать уже целенаправленно, а значит, строить диагностическое заключение более совершенно.
Коэффициенты разложения — важная информация об эволюции сигнала. Они зависят от выбора изначального всплеска. Для каждой прикладной задачи можно подобрать наиболее приспособленный (именно для нее) всплеск. Он как раз и называется Вэйвлетом. Математическая сторона вэйвлет-анализа — вещь довольно тонкая, можно сказать сложная, хотя и весьма наглядная. А вот прикладная сторона вэйвлетов очень простая. Применение вэйвлетов для исследования биомедицинских сигналов, которые имеют развертку во времени или меняют свою частоту, началось сравнительно недавно. Например, медицинская диагностика — изучение скорости кровотока, скорости пульсовой волны или частоты дыхания активно использует алгоритмы вэйвлет-анализа. Мода на использование дискретного Wavele t -преобразования (DWT или иначе WT) в задачах биометрии условно начинается с середины 90-х гг. Следует отметить, что WT не является “полноценным” преобразованием сигнала из временной в частотную область. Чтобы было легче представить, что это такое, отметим, что результат похож на фильтрацию в октавных полосах частот. Не рассматривая детали этой процедуры, отметим, что фактически здесь также приходится вводить понятие фрагмента — октавы. Такое понятие опять позволяет связать уже известные представления СКА и Wavelet-преобразования. Связь между частотной полосой осуществляется через параметр масштаба, который влияет на сжатие/растяжение базовой вэйвлет-функции. Количество частотных полос для дискретного WT определяется как log2(N), где N =2 m опять размер блока в элементах, определяющих размер фрагмента или октавы. При N =2048 получим 11 частотных полос. Самая высокочастотная полоса простирается от 1/4 до 1/2 от частоты дискретизации. Предыдущая частотная полоса — от 1/4 до 1/8 от частоты дискретизации и т. д. до самых низких частот. В первом приближении можно говорить о WТ как о полосовых фильтрах. Однако это сходство очень обманчиво, поскольку WT осуществляется принципиально иначе по сравнению с той же цифровой фильтрацией. Массив “однополосного” результата WT часто называется коэффициентами WT. Здесь следует пояснить, что для фильтрации сигналов с помощью WT просто обнуляются коэффициенты, соответствующие частотной полосе, в которой присутствуют нежелательные компоненты, а затем выполняется обратное преобразование, что дает отфильтрованный сигнал во времени. Окно фильтрации как бы сжимается во времени при переходе к более высоким частотам. Преимущества WT проявляются в спектральном анализе нестационарных сигналов. Используя WT, можно получить импульсные функции отклика на разных частотах. В отличие от традиционных аналоговых и цифровых фильтров, WT имеет короткий по времени переходной процесс на импульсные воздействия. Математический аппарат WT не так прост, как может показаться на первый взгляд, а настройка параметров еще более трудоемка, чем для БПФ. Изменив тип базового вэйвлета, можно получить иной результат в зависимости от специфики сигнала. Именно поэтому интерпретация результатов WT доступна опытным экспертам и в настоящее время является самостоятельной задачей при выборе этого направления. Анализ данных посредством WT может быть сравним с обычными классическими статистическими методами. Для получения спектральной оценки первоначально вычисляют среднеквадратичное значение по каждой группе коэффициентов, в противном случае результаты WT следует интерпретировать как подобие спектрограммы. Таким образом, само по себе WT — скорее масштабно-временное преобразование сигнала с разложением в различных частотных полосах, нежели преобразование из временной области в частотную область представления сигнала, как в случае БПФ. Разложение исходного сигнала осуществляется обычно с помощью вэйвлет-функций, вид которых определяется второй производной от функции распределения Гаусса. Впрочем, возможны и другие функции, например, обладающие фрактальными свойствами. В этом смысле WT-анализ близок СКА. Возможность использования фрактального представления данных WT-анализа сегодня представляется интересным направлением. Однако переход от WT-анализа, результатом которого является вычисление некоторых показателей исследуемого процесса, к построению фрактальных кривых осуществляется достаточно сложно. Реализация такого перехода очень часто сопровождается использованием эвристических алгоритмов, которые затрудняют интерпретацию результата, но порождает интересные графические образы. Заключение Методы анализа данных медицинского обследования представляют значительный интерес для различных практических задач. Для разработчиков таких методов это направление открывает новые возможности в познании скрытых механизмов деятельности живого организма, а для практиков — медицинского персонала — позволяет быстро и надежно не только распознать имеющиеся нарушения, но и выбрать эффективный и надежный путь лечения. Медицинский диагноз — прежде всего классификационная задача. Среди множества различных состояний живого организма можно условно установить два класса: “норма” и “нарушение”. Такие понятия, в свою очередь, требуют уточнения и введения дополнительных понятий, раскрывающих тот или иной класс. В ряде практических случаях, по данным многолетних наблюдений и исследований живого организма, удается сформулировать понятие нормы в терминах математической статистики. Установить так называемый среднестатистический показатель, характеризующий нормальное состояние организма в целом или его отдельной подсистемы. Типичным примером может служить температурный показатель, который формируется посредством традиционной процедуры измерения температуры тела в установленных точках. Для поверхности тела принято считать “нормой”, когда значение температуры не превосходит значения 37 ° С, а например, для полости рта этот показатель составляет 32 ° С. При исследовании сердечно-сосудистой системы пользуются показателем — частота пульса, который может быть определен по данным пульсометрического или электрокардиографического исследования. Важным показателем является и величина артериального давления, скорость распространения пульсовой волны и целый ряд других. На практике часто представляет интерес процедура оценки общего состояния организма, которая выполняется простыми и доступными средствами для большого количества людей. Это так называемая процедура экспресс диагностики. В повседневной жизни такая процедура оказывается чрезвычайно важной, так как обеспечивает выбор правильного — рационального поведения живого организма. Несмотря на относительную простоту пульсометрической или кардиографической процедуры, в результате которой можно получить некоторый массив данных, отражающих работу сердечно-сосудистой системы, анализ таких данных всегда проводится по определенным правилам — алгоритмам. В том случае, когда рассматривается задача построения оценки общего функционального состояния организма, такой анализ можно проводить посредством разделения технических и вычислительных ресурсов. Используя простейший датчик регистрации биосигнала с поверхности живого организма, производить дальнейший анализ в специализированном центре. Принимая во внимание, что анализ можно проводить по заранее выбранным алгоритмам, целесообразно такую процедуру осуществлять на удаленном компьютере, подключенным в сеть обслуживания абонентов. Такое решение задачи о предоставлении услуг медицинской диагностики при массовых запросах целесообразно проводить на основе сети Интернет. Телемедицинская услуга — оценка текущего состояния организма, реализуемая на основе традиционных автономных средств индивидуальной связи, например сотового телефона, в котором предусматривается регистрация пульсометрических данных, становится одной из востребованных и универсальных услуг. Знание основных принципов построения решающих правил в процедуре формирования медицинского диагностического решения представляется актуальной задачей. Умение правильно выбрать информационные параметры о состоянии организма и построить медицинское заключение позволяет построить техническую телемедицинскую систему, обеспечивающую осуществление выбора в процедуре опознания состояния организма. Понятие “норма” и “отклонение” от нормы, как правило, формируются на математическом языке в определенных терминах. С позиции математического анализа состояния организма такое понимание вопроса вполне корректно. Медицинская практика имеет другие взгляды на эту тему. Прежде чем приступить к формированию диагностического решения, врач – медик производит сбор данных о состоянии организма конкретного пациента. Такая процедура часто проходит на описательном уровне. Это так называемое вербальное – словесное описание состояния организма, которое включает как личные наблюдения врача, так и различные высказывания самого пациента. Добавлением к этим данным служат многочисленные результаты клинических и лабораторных исследований. Такие данные также могут быть представлены как в количественной форме, так и виде обширных словесных описаний. На основе такого материала и происходит формирование диагностического решения. Формально можно говорить, что медицинский диагноз представляет собой некоторую процедуру поиска. Исполнение такой процедуры направлено на решение двух задач. В первом случае отыскивается ответ по поводу наличия или отсутствия некоторого заболевания. В другом, более сложном случае, отыскиваются причины появления указанного заболевания. В структурном отношении процедура поиска диагностического решения имеет много уровней, связанных между собой определенными правилами перехода. Это так называемое дерево возможных альтернативных путей отыскания верного решения. В математике такое представление о процедуре поиска носит название графа, на концах ветвей которого находятся конечные решения. Процесс постановки диагноза в таком случае представляется как движение по стволу и ветвям дерева от одного разветвления к следующему. Возможность перехода на следующее состояние определяется результатом, полученным на предыдущем уровне. В таком понимании медицинский диагноз можно представить в виде системы тестов, исполнение которых автоматически приводит к искомому результату. Принимая во внимание, что количество тестов может быть достаточно большим, процесс отыскания требуемого решения целесообразнее вести с помощью компьютера. В этом случае необходимо помнить, что увеличение количества тестов будет способствовать получению более точного диагностического решения, но при этом возрастает время анализа. И, это достаточно часто встречается на практике, предложенная процедура отыскания диагностического решения растягивается на очень большой промежуток времени, когда сам результат уже не имеет практического значения. Другими словами, процесс поиска нужного эффективного решения оказался слишком длинным и к этому времени организм либо уже погиб, либо характеризуется новыми показателями состояния. Понимание этого явления выдвигает определенные требования к времени формирования диагностического решения. Период формирования диагностического решения должен быть меньше продолжительности исследуемого процесса. Кроме того, формируемые в процессе диагностической процедуры показатели состояния организма должны обеспечивать возможность построения прогноза. В таком понимании диагностической процедуры можно утверждать, что основой для его постановки является описание состояния организма и непременно условий окружающей среды. В ряде случаев к этому добавляются физико-химические показатели среды, географические координаты местности и другие факторы, косвенно влияющие на психофизиологические параметры организма. На практике для решения этой многоплановой задачи используются так называемые “обучающие выборки данных”. На основе известных показателей о функциональном состоянии организма формируются образы “нормы” и “патологии”. Описания таких образов в терминах выбранной математической модели запечатлеваются в памяти компьютера. В последующем, при предъявлении текущих — других данных о состоянии организма, в терминах математической модели строятся оценки по отличию от нормы. Из этого примера отчетливо видно, что в медицинской практике очень часто возникает задача не построения диагностического правила по известным признакам нарушения, а выбор диагностических признаков на фоне большого количества данных о состоянии организма. Другой, немаловажный аспект медицинской диагностики состоит в том, что в реальной практике невозможно собрать полный и обширный материал изучаемого нарушения. Здесь проявляется особенность медицинских данных обследования, выражающаяся в том, что формирование класса “норма” или “патология” не может продолжаться бесконечно долго. При этом допускается, что такие классы образуются из бесконечного множества подгрупп. Так на примере электрокардиографического исследования (ЭКГ) сердечной деятельности может быть поставлен вопрос о продолжительности этой процедуры. Какое минимальное время требуется для проведения ЭКГ процедуры, чтобы диагностическое решение имело высокий уровень достоверности? Это, безусловно, важный вопрос, который характерен практически для всех диагностических процедур. Ответ на такой вопрос в каждой конкретной диагностической процедуре устанавливается на основе учета многих факторов, в том числе и технических характеристик медицинской аппаратуры. Эти проблемные вопросы являются типичными для медицинской диагностики, преодоление которых осуществляется на этапе создания алгоритмов диагностических процедур. Интерес человека к природным объектам, явлениям и процессам проявляется в построении моделей. Организм человека, его различные функциональные характеристики, проявляющиеся в течение всей жизни, всегда были предметом детального изучения. Познание особенностей работы отдельных подсистем организма человека направлено на оценку функционального состояния, которое может изменяться как в процессе совершения некоторой работы, так и с течением времени. Медицинская диагностика, рассматривающая эти вопросы, позволяет построить такую оценку, используя специальные методы обследования живого организма. Современная медицинская практика накопила большой материал о различных нарушениях, наблюдающихся в организме. Выявление таких нарушений, как правило, происходит на основе различных моделей, построенных в терминах математики, биофизики, биохимии. Применение статистического и многофакторного метода анализа данных в задачах медицинской диагностики позволяют получить определенные результаты, однако, как сейчас становится очевидным, такие оценки могут быть получены в ограниченных случаях. Понимание того, что обычные и традиционно используемые методы построения диагностических решений применимы только в простейших случаях, пришло сравнительно недавно. Переход на новые рубежи понимания развития живых организмов произошел на рубеже 22 и 21 столетия. Основными элементами, обеспечившими такой переход, явились современные компьютерные технологии и концепция развития диссипативных систем. Применение компьютеров в медицинской практике позволило не только повысить эффективность медицинской диагностики, но и “увидеть” новые перспективные направления ее развития. Развитие Интернет технологий предоставления различных услуг оказывает существенное влияние на все области практической деятельности человека. Медицинские услуги, предоставляемые в сети Интернет, стремительно развиваются в фармакологической и консультационной, экспертной области. Формирование типовых диагностических заключений по запросу удаленного абонента сети происходит все в больших масштабах. Организация работ по медицинской диагностике в сети Интернет активизируется на больших узлах связи — Провайдерских центрах. Рассмотренные в учебном пособии тематические направления современного развития медицинской диагностики, реализуемой в среде Интернет, позволяют приобрести необходимые знания для эскизного проектирования алгоритмов и программ анализа биометрических данных.
Литература
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.101 (0.05 с.) |
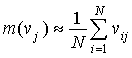 .
.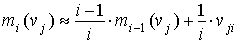 .
.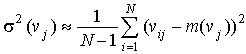 .
.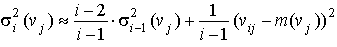 .
.