
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи оптимизации конструктивных характеристик артиллерийского орудия ⇐ ПредыдущаяСтр 9 из 9
По сравнению с задачами, составляющими модель проектирования артиллерийского комплекса(обоснование типажа, сроков начала разработки, ТТХ), оптимизация конструктивных характеристик арторудия выступает на более низком уровне. При постановке и решении задачи выбора оптимальных ВТХ одновременно решается и задача выбора оптимальных конструктивных параметров арторудия. Это связано с рассмотрением набора альтернатив. Вместе с тем, альтернативы конструкции арторудия формулируются настолько подробно, насколько, с одной стороны, целесообразно усложнять процесс вычисления, а с другой — насколько критичны используемые интегральные критерии (критериальные функции задачи выбора оптимальных ТТХ) к вариациям конструктивных параметров орудия, характеризующих различные альтернативы. При этом достаточно подробно решается только задача баллистического проектирования ствола арторудия. Более же глубокая проработка конструкции арторудия требует решения большого числа взаимосвязанных задач. Предварительный анализ показывает, что имеет место определенная иерархия проектных задач и критериев (целевых функций): — на первом уровне применяются интегральные критерии — стоимость, характеристики боевой эффективности; ―на втором уровне в качестве критериев используются требования, предъявляемые к ТТХ арторудия — критерии качества функционирования по надежности, стабильности, точности, мобильности и т. п.; ―на третьем уровне — частные критерии, характеризующие функционирование агрегатов арторудия, отдельные процессы (при этом характерно разнообразие критериев, вытекающее из многообразия задач синтеза конструкции арторудия). Между рассмотренными критериями существует определенное взаимоподчинение: критерии первого уровня определяют цели задач, решаемых на втором и третьем уровнях; критерии второго уровня влияют на формирование критериев, используемых при решении задач третьего уровня. Наряду с указанными прямыми связями имеют место и обратные зависимости, которые определяют необходимость уточнения, корректировки, так как для прямых связей будет характерным также отсутствие полноты и достаточности математических зависимостей между критериями. Наличие прямых и обратных связей обусловливает необходимость итераций.
Высокая размерность задачи синтеза арторудия, наличие большого количества прямых и обратных связей между отдельными подсистемами, сложность глобальной целевой функции, а также вычислительные проблемы требуют рассмотрения процесса проектирования артсистем с позиций теорий сложных систем, представления его в виде определенной последовательности этапов и уровней решения отдельных задач. Степень детализации и количество уровней определяются анализом целевого назначения традиционных задач, составляющих процесс проектирования. Для исследования проектирования арторудий с позиций многоуровневого системного подхода имеются следующие предпосылки: — практикой проектирования арторудий разработана достаточно подробно математическая модель, описывающая основные процессы, протекающие при функционировании артсистемы; при этом отдельные задачи, отработанные до уровня их решения на ЭВМ, могут служить элементами для системных построений; — постоянно совершенствуются математические методы оптимизации; — разработана общетехническая база системных исследований. Проектирование арторудия как сложной иерархической структуры, состоящей из взаимосвязанных подсистем, характеризуется рядом особенностей: Одна из них — сведение взаимодействия между подсистемами иерархической структуры к некоторым схемам сопряжения, позволяющим имитировать взаимодействие процессов функционирования подсистем. Построение схем сопряжений — один из важнейших этапов многоуровневого системного проектирования. Один из возможных подходов при этом заключается в анализе вклада, который вносят вариации тех или иных обобщенных параметров арторудия (характеристик надежности, стабильности, тактико-технических характеристик и т.п.) и частных параметров (технических и конструктивных характеристик агрегатов и узлов орудия) в изменение интегрального критерия, например показателя эффективности артсистемы. При этом предполагаются известными зависимости Э = Э(
где Э —показатель эффективности системы, {
Приращение критерия
Аналогично
Тогда
где В частных случаях для описания связей между критерия 1, 2 и 3 уровней возможно применение известныхсхем компромиссов. Простейшие из них сводятся к построению обобщенного критерия эффективности (целевой функции) как некоторой скалярной функции частных критериев эффективности. При этом подходе (называемом иногда свертыванием векторного критерия) задача сравнения решений по векторному критерию фактически заменяется задачей выбора способа свертывания и определения значения коэффициентов, участвующих в этом свертывании. Способы свертывания, отражая ту или иную схему компромисса, могут существенно отличаться друг от друга. 1. Аддитивный критерий. В этом случае в качестве обобщаемого критерия берется «взвешенная» сумма частных критериев: Э= где п — количество частных критериев эффективности Fj. При использовании аддитивного критерия в качестве Э может выступать, например, стоимость или вес орудия, а в качестве Fj, соответственно, стоимость и вес отдельных частей орудия. 2. Мультипликативный критерий. «Взвешенное» произведение частных критериев Э == В этом случае в качестве Э может использоваться вероятность безотказной работы арторудия. При этом, Fj будут показатели безотказности отдельных узлов и агрегатов орудия. В качестве мультипликативного критерия могут использоваться также рассмотренные ранее зависимости для стоимости орудия. 3. Конъюнктивный критерий оценивает каждое решение с точки зрения цели, степень достижения которой (с учетом «весового» коэффициента) в данном случае наименьшая: Э = В качестве примера конъюнктивного критерия может расссматриваться коэффициент запаса прочности элементов арторудия. В этом случае Э- коэффициент запаса прочности такого элемента орудия, для которого он имеет минимальное значение. 4. Дизъюнктивный критерий противоположен предыдущему и оценивает решения с точки зрения цели, степень достижения которой (с учетом «весового»коэффициента) в данном случае максимальна: Э = Таким критерием может выступать вероятность отказа элемента арторудия, для которого она имеет максимальное значение. В рассмотренных зависимостях 5. Выделение наиболее важного критерия. В этом случае из набора частных критериев эффективности выделяется один, который и принимается за обобщенный. Остальные рассматриваются как критерии допустимости,и на значения каждого из них накладывают дополнительные ограничения вида Fj
При назначении пределов по каждому из критериев обычно исходят из особенностей конкретной задачи. Так, в методе «уступок» эти пределы задают указанием по каждому критерию некоторой «уступки» допустимому значению этого критерия по сравнению с его наилучшим возможным значение (Ff*), т. е. Fj = Ff* + После того, как выбран критерий, построена модель и определена исходная информация, необходимо найти оптимальное решение. При рассмотрении ранее задач выбора оптимальных типажа и ТТХ артсистем, были отмечены особенности, связанные с необходимостью организации поискового процесса. Решение задач оптимизации конструктивных характеристик арторудия также строится на базе математических методов оптимизации. Выбор метода оптимизации зависит, как от особенностей рассматриваемой задачи, так и от возможностей используемых вычислительных средств.
4.3.1. Сведения о методах нахождения оптимальных решений. В зависимости от наличия и вида ограничений, количества этапов в операции и формы модели находят применение те или иные виды математического программирования, хотя одна и та же задача может быть решена разными методами. Смысл терминологии и символики, используемой при рассмотрении методов оптимизации, раскрывается на примере возможных постановок оптимизационных задач применительно к процессу движения откатных частей арторудия. Модель процесса:
где х — перемещение откатных частей; М0 — масса откатных частей; тпр— масса механизмов автоматики, приведенная к массе откатных частей; Ркн — сила действия пороховых газов на дно канала ствола; R — приведенная сила сопротивления движению откатных частей.
Целевая функция (критерий оптимизации) F = F (х, у, и, a t), где х,у -параметры состояния системы; и — параметры управления системы; а -неуправляемые параметры; t—независимая переменная (время). Примеры целевой функции: 1.F= где
2. F= (max Ф) где max Ф -максимальное значение силы гидравлического сопротивления. Ограничения: х, у Х Примеры функции управления и: 1) u 1 =P кн (t); u.2=R(x,dx/dt,t); 2) и = R(x, dx/dt, t); 3) и= a (х) (переменная площадь отверстия истечения жидкости). Примеры неуправляемых параметров α: Р н0—начальное усилие поджатия пружины накатника; сн— жесткость пружины накатника; D0 — внутренний диаметрцилиндра тормоза отката; l — длина веретена тормоза отката и т. п. Методы математического программирования можно разделить на две группы: аналитические и численные. Аналитические — это дифференциальное и вариационное исчисление, принцип максимума Понтрягина. Численные— это линейное, нелинейное и динамическое программирование, методы регулярного и случайного поиска. Для использования аналитических методов необходимо, чтобы расчетная формула критерия, ограничения и связи между координатами, управлениями и независимой переменной, а также начальные и конечные условия были представлены в форме функций, которые должны быть, по крайней мере, один раз дифференцируемы и иметь конечное число точек разрывов. При этом, для использования классических методов (дифференциального и вариационного исчисления) обязательно отсутствие ограничений. Если имеются ограничения и управление является функцией независимых переменных а модель представляет собой набор аналитических зависимостей, то может применяться принцип максимума Понтрягина, являющийся развитием и обобщением задач вариационного исчисления. Этот принцип позволяет решать задачи при наличии ограничений на управления и при любыхсвязях между переменными (в том числе и неголономных, т.е. включающих производные). Дифференциальное исчисление оперирует известными методами анализа экстремальных значений функций. Вариационное исчисление изучает методы нахождения экстремума функционалов. Пусть Ω — множество функции и каждой функции φ(х), принадлежащей Ω(φ(x) J(y)= где х, у(х), z (x) связаны дифференциальным уравнением
В качестве задачи на нахождение оптимальных значений параметров управления с использованием принципа максимума, разработанного Л. С. Понтрягиным, можно рассмотреть приведенный ранее пример, относящийся к процессу движения откатных частей. Предполагается наличие всех условий, выполнение которых необходимо для применения аналитических методов, и введение функции цели в виде F=
Если условия применимости аналитических методов не выполняются или решение задач связано с серьезными вычислительными трудностями, то применяются численные методы оптимизации. При этом, если критерий (целевая функция) представляет собой линейную функцию управлений, а управления (переменные) подчинены линейным ограничениям, то имеет место задача линейного программирования. Например: минимизировать
Для решения задачи линейного программирования разработано много методов, как конечных (гарантирующих нахождение точного решения за конечное число шагов), так и итеративных (гарантирующих лишь приближенное решение задачи). Основной вычислительной схемой, позволяющей отыскать оптимальное решение задачи линейного программирования, является симплексный метод (симплексом называется п-мер ный выпуклый многогранник, имеющий в точности (п + 1) вершин). Решение отыскивается обычно за т Если к Хк предъявляются требования целочисленности, то используются разработанные алгоритмы решения: методы Гомори и Балоши. В случае, если F = (x 1.... xk), где на F не наложено требование линейности, имеет место задача нелинейного программирования. Нелинейное программирование разделяется на выпуклое и невыпуклое. Если функция цели F — выпуклая (вниз) функция своих переменных, а ограничения определяют выпуклое множество, то это задача выпуклого программирования. Основная особенность заключается в том, что ее локальные экстремумы совпадают с глобальным экстремумом (одноэкстремальная задача). В задачах невыпуклого программирования локальный экстремум достигается, как правило, в большом количестве точек (многоэкстремальная задача). Пример задачи нелинейного программирования— задача распределения Nop орудий по N ц различным целям, где Р Необходимо обратить в максимум математическое ожидание ущерба, наносимого противнику:
F=
где Функция F не линейна по переменным Х ij и невыпукла. Хотя сформулированная задача является целочисленной, ее можно рассматривать и как непрерывную, если номеру i соответствует не одно орудие, а целая батарея из Алгоритмы решения на ЭВМ. задач нелинейного программирования разработаны для случаев, когда: F— дважды дифференцируемая; F — вогнутая, ограничения тоже вогнутые функции; F — полином 2-й степени, а ограничения линейны. Для решения задач нелинейного программирования используются методы поиска. Рассмотренные методы линейного и нелинейного программирования относятся к одношаговым процедурам оптимизации. Для исследования многоэтапных процессов используется динамическое программирование. Особенности таких задач следующие: задача должна допускать возможность интерпретировать ее как k-шаговый процесс принятия решений; решение для k-шаговой задачи получается из решения (k—1)-шаговой задачи путем добавления k-го шага и использования результата, полученного для (k—1) шагов. Выбор значения управляющей переменной на k -м и в k-шаговом процессе не должен влиять на предшествующие (k —1) шаги. Если эти условия выполнены, то решение k-шаговой задачи может быть сведено к решению следующей последовательности задач: сначала одношаговой, потом двухшаговой, трсхшаговой и вплоть до k-шаговой. В качестве примера задачи динамического программирования может быть рассмотрено, например оптимальное распределение допусков. Исходные сведения: Известной предполагается зависимость выходного параметра системы х = x( D (x) =
— минимальное значение среднего квадратического отклонения параметра элемента, которое может быть достигнуто на современном этапе развития техники (ограничение по минимальному разбросу параметров);
Так как в целом системный параметр связан с параметрами элементов, и для обеспечения заданной надежности должна быть соблюдена заданная дисперсия, то общий максимум выигрыша но запасу допусков может быть выполнен, если F = L ( Ограничения: В качестве этапов выбираются этапы, связанные с количеством участвующих в решении параметров элементов (на первом этапе предполагается, что весь «запас» допуска системы использован только на один элемент (любой), на втором - на два и т.д. и что в это время остальные элементы, абсолютно стабильны). Сначала некоторое «количество» допуска в пределах (0, Методы поиска (регулярного или случайного) могут быть применены для решения любой одноэтапной задачи математического программирования. Возможности этих методов ограничены трудоемкостью расчетов. Под регулярным (детерминированным) алгоритмом поиска подразумевается такая система действий, которая строго предопределяется сложившейся ситуацией. Существует много методов регулярной оптимизации многопараметрических систем. Для методов поиска обязательно наличие ограничений. Метод сканирования (слепой поиск)— это последовательный перебор состояний При работе но методу сканирования всегда находится глобальный экстремум. Это достоинство часто заставляет обращаться к сканированию, несмотря на его неэкономичность. Метод поочередного изменения параметров (метод Гуасса — Зейделя) — это поочередная оптимизация по каждому регулируемому параметру объекта. Сначала оптимизация производится по одному параметру, затем переходят ко второму и так далее до тех пор, пока функция качества не перестает уменьшаться. Метод плохо работает в районе «оврага». Метод градиента. Система побуждается к движению в антиградиентном направлении, т. е. в направлении, обратном вектору градиента функции качества: F = F grad F = Вектор градиента определяет направление наибольшего возрастания функции качества. Поэтому этот метод является оптимальным в том случае, если он стимулирует движение системы в наилучшем направлении. Поиск по методу градиента разбивается на два этапа. На первом этапе определяются составляющие градиента где Затруднено применение метода при наличии ограничений, накладываемых на зону поиска, по мере приближения к цели, а также по причине уменьшения скорости движения. Метод наискорейшего спуска — это развитие метода градиента. При спуске делается шаг в направлении, обратном grad. Если значение функции при этом уменьшилось по сравнению с исходным, то делается очередной рабочий шаг в том же направлении, а не определяется заново grad. Метод тяжелого шарика (учитывает предысторию поиска). Вводится «инерция» в процессе поиска, которая отражает осредненное ближайшее прошлое. Поиск, таким образом, становится глобальным. Набрав скорость в определенном направлении, система за счет инерции может «проскальзывать» локальные экстремумы и, следовательно, способна попасть в наименьший из них. В применении градиентных методов имеются существенные трудности: ‑ предполагается гладкость функции F, т. е. существование у нее частных производных во всех точках, что практически не всегда реально; ‑ даже если градиент существует, его вычисление может оказаться слишком трудоемким. Случайный поиск. Преимущества методов случайного поиска перед регулярными возрастают по мере увеличения сложности (размерности) функционала (процесса) и по мере уменьшения требуемой точности отыскания экстремума. Методы не зависят от вида оптимизируемой функции. Слепой поиск. После выполнения п шагов из всего множествазначений функций выбирается наименьшее. Последовательный поиск. Сущность метода заключается в следующем. Из точки у в заданной области изменения параметров делаются случайно направленные пробные перемещения. Если в результате найдена точка, лежащая в данной области, причем такая, что в ней значение функции качества F больше, чем в точке у, то в этом случае переходят в найденную новую точку. Если не удается найти точку лучшую, чем у, а количество неудачных попыток достигло некоторой заранее заданной величины, тогда уменьшается шаг пробных перемещений и поиск лучшей точки продолжается, но уже в меньшей окрестности точки у. В конце концов либо отыскивается точка лучше, чем у, либо шаг поиска становится меньше некоторого минимального шага, и тогда можно считать, что искомый максимум находится в точке у. Для составления алгоритма случайного поиска используется понятие m-мерного случайного вектора, отдельные реализации которого направлены равновероятно во всех направлениях пространства параметров, т.е. ξ=
При Fi > Адаптивный поиск (с обучением). Рассматривается один из возможных алгоритмов поиска с обучением. Пусть
найти Пусть ξ= После каждого шага по В качестве ξ(
Начальные данные для 1 шага: H= h= 1, r = Чтобы не выйти за пределы интервала поиска, нужно иметь H= Решение задач математического программирования значительно усложняется, если приходится иметь дело со случайными функциями или величинами. Разрабатываются методы стохастического программирования (методы поиска при наличии «шумов» и др.), методы стохастической аппроксимации. В последнее время уделяется внимание развитию методов эвристического программирования (при этом используется опыт специалистов данной области, формализуемый в виде некоторых правил). Эвристическое программирование дает возможность найти решение (не обязательно оптимальное) в тех случаях, когда классические методы программирования бессильны (например, в задачах большой размерности).
4.3.2. Примеры задач определения оптимальных конструктивных характеристик элементов артиллерийского орудия при использовании целевых функций частного вида Формулировка задач оптимизации в терминах математического программирования Формулировка задач оптимизации в терминах математического программирования предполагает, прежде, всего, четкую классификацию параметров, на которых построены математические модели оптимизируемых объектов. При этом различают три характерные группы параметров. 1. Конструктивные параметры. Это независимые друг от друга (или слабо зависимые, взаимной зависимостью которых можно пренебречь) конструктивно настраиваемые, переменные. В процессе проектирования стремятся выбрать численные значения этих параметров так, чтобы наилучшим образом удовлетворить техническим требованиям, предъявляемым к конструкции. Указанные переменные, таким образом, можно изменять воздействуя тем самым па выходные свойства проектируемой конструкции в желаемом направлении. На конструктивные параметры, как правило, накладываются двусторонние ограничения, обусловленные конструктивно-компоновочной, технологической или эксплуатационной осуществимостью проектируемого объекта. 2. Параметры состояния. Это выходные свойства конструкции, ее отклик. Они характеризуют поведение. объекта. Параметры состояния регламентируются техническими требованиями. Последние представляются в виде односторонних или двусторонних ограничений на параметры состояния. 3. Параметры внешней среды. Это независимые друг от друга (или слабо зависимые, взаимной зависимостью которых можно пренебречь) параметры, характеризующие среду, в которой протекает жизненный цикл проектируемого объекта. Параметры среды, так же, как и конструктивные параметры, определяют его поведение. Параметры среды обычно задаются на некотором интервале в виде двусторонних ограничений. К числу подобного рода параметров относят и промежуток времени, в котором развиваются анализируемые процессы, режимы функционирования объекта и т. п. Одной из особенностей свойств внешней среды является то, что они могут быть сл
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 48; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.162 (0.087 с.) |
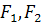 ,..., Fn),
,..., Fn),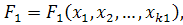
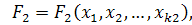
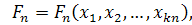
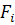 } —совокупность обобщенных параметров орудия, {
} —совокупность обобщенных параметров орудия, { 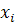 }—совокупность частных параметров.
}—совокупность частных параметров.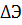 из-за изменения обобщенных параметров может быть выражено полным дифференциалом в конечных разностях:
из-за изменения обобщенных параметров может быть выражено полным дифференциалом в конечных разностях: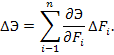
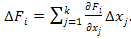
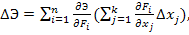
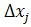 — приращение значения j-го частного параметра орудия,
— приращение значения j-го частного параметра орудия, 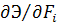 — коэффициент влияния i-го обобщенного параметра арторудия на его эффективность,
— коэффициент влияния i-го обобщенного параметра арторудия на его эффективность, 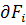 /
/ 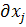 — коэффициент влияния j-го частного параметра арорудия на его эффективность.
— коэффициент влияния j-го частного параметра арорудия на его эффективность.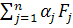 ,
,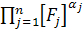 .
.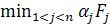 .
.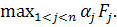
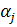 — неотрицательные коэффициенты, значения которых выбираются исходя из степени важности отдельных целей. При их назначении можно воспользоваться анализом ранее решенных аналогичных проектных задач или методом проб
— неотрицательные коэффициенты, значения которых выбираются исходя из степени важности отдельных целей. При их назначении можно воспользоваться анализом ранее решенных аналогичных проектных задач или методом проб 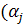 подбираются при анализе результатов, получаемых при различных значениях этих коэффициентов).
подбираются при анализе результатов, получаемых при различных значениях этих коэффициентов).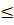 Fj.
Fj.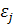 . Метод последовательных уступок предполагает, что все количественные цели и соответствующие им критерии можно упорядочить (и перенумеровать) в порядке убывания их значимости. Рекомендации по выбору проектного решения получаются в результате решений последовательности k задач, причем, в j-й задаче (j=
. Метод последовательных уступок предполагает, что все количественные цели и соответствующие им критерии можно упорядочить (и перенумеровать) в порядке убывания их значимости. Рекомендации по выбору проектного решения получаются в результате решений последовательности k задач, причем, в j-й задаче (j= 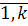 ) в качестве целевой функции выступает j-и критерий, и на значения первых (j-1) критериев наложены дополнительныеограничения вида Fi
) в качестве целевой функции выступает j-и критерий, и на значения первых (j-1) критериев наложены дополнительныеограничения вида Fi 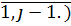 Значение каждой из величин Fi определяется по результатам решения соответствующей i-й задачи, например, путем указания величины уступки
Значение каждой из величин Fi определяется по результатам решения соответствующей i-й задачи, например, путем указания величины уступки 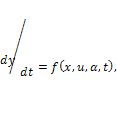
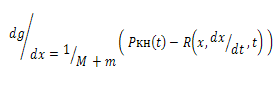
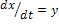
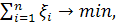
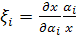 - безразмерный коэффициент чувствительности.
- безразмерный коэффициент чувствительности.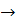 min,
min,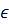 G, Gy; и
G, Gy; и 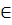 Ω), поставлено в соответствие определенное число. Тогда говорят, что на множестве Ω задан функционал. Общей задачей вариационного исчисления является задача максимизации или минимизации функционала вида
Ω), поставлено в соответствие определенное число. Тогда говорят, что на множестве Ω задан функционал. Общей задачей вариационного исчисления является задача максимизации или минимизации функционала вида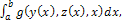
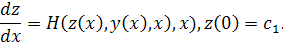
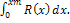 При этом R(x) рассматривается как управление.
При этом R(x) рассматривается как управление.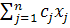 при условиях
при условиях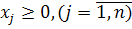 ;
; 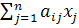 = bi (i =
= bi (i = 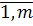 ).
).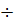 2т шагов.
2т шагов.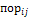 —вероятность поражения j-й цели i-м орудием при закреплении его за этой целью;
—вероятность поражения j-й цели i-м орудием при закреплении его за этой целью; 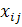 — числа, характеризующие план распределения и принимающие значение 1, если i-e средство закрепляется за j-й целью, и значение 0 в противном случае; ограничения: Xij
— числа, характеризующие план распределения и принимающие значение 1, если i-e средство закрепляется за j-й целью, и значение 0 в противном случае; ограничения: Xij 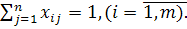
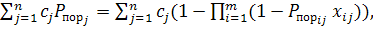
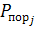 -вероятность поражения j-й цели; Cj — важность j-й цели.
-вероятность поражения j-й цели; Cj — важность j-й цели.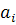 орудий.
орудий.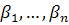 ) от конструктивных параметров элементов
) от конструктивных параметров элементов 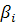 (i =
(i = 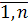 );
);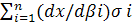 — дисперсия системного параметра;
— дисперсия системного параметра;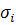 — среднее квадратическое отклонение эксплуатационного допуска i -г o параметра элемента;
— среднее квадратическое отклонение эксплуатационного допуска i -г o параметра элемента;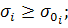
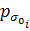 (
(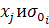 в указанном диапазоне;
в указанном диапазоне;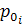 (
( 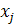 с
с 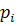 (
(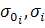 ) =
) = 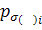 (
(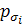 (
(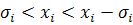 ) -общая вероятность выигрыша по запасу допуска i -го параметра (для получения наибольшего запаса по
) -общая вероятность выигрыша по запасу допуска i -го параметра (для получения наибольшего запаса по 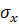 и
и 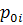 была минимальной, а вероятность
была минимальной, а вероятность 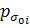 —максимальной).
—максимальной).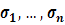 )=
)= 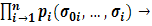 max обратится в максимум.
max обратится в максимум.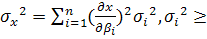 0.
0.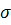 х ) назначается n-му процессу, затем (n—1)- му и т.д.; тем самым вводится динамический процесс распределения. На каждом этапе отыскивается условное оптимальное управление(при всевозможных предположениях о результатах предыдущего шага), а затем, когда процесс доведен до нулевого состояния, снова повторяется вся последовательность шагов, но уже из множества условных оптимальных управлений выбирается одно.
х ) назначается n-му процессу, затем (n—1)- му и т.д.; тем самым вводится динамический процесс распределения. На каждом этапе отыскивается условное оптимальное управление(при всевозможных предположениях о результатах предыдущего шага), а затем, когда процесс доведен до нулевого состояния, снова повторяется вся последовательность шагов, но уже из множества условных оптимальных управлений выбирается одно.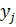 из множества допустимых
из множества допустимых 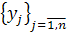 . При этом запоминается наименьшее значение функции качества
. При этом запоминается наименьшее значение функции качества 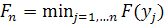 и состояние, приведшее к этому наименьшему значению. В соответствии с алгоритмом это состояние заменяется другим только в случае, если новое значение показателя качества окажется меньше, чем значение, хранимое в памяти.
и состояние, приведшее к этому наименьшему значению. В соответствии с алгоритмом это состояние заменяется другим только в случае, если новое значение показателя качества окажется меньше, чем значение, хранимое в памяти.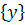 ,
, 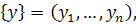
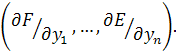
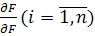 , на втором — система делает рабочий шаг, т. е. смещается в направлении, обратном градиенту:
, на втором — система делает рабочий шаг, т. е. смещается в направлении, обратном градиенту: 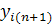 =
= 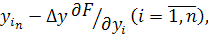
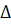 у — параметр длины рабочего шага.
у — параметр длины рабочего шага.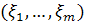 , где
, где 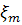 случайные равномерно распределенные числа в интервале (—1-:-1). Алгоритм случайного поиска с возвратом записывается следующим образом:
случайные равномерно распределенные числа в интервале (—1-:-1). Алгоритм случайного поиска с возвратом записывается следующим образом: 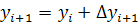 , где
, где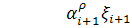 при
при 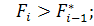
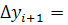 -
- 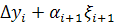
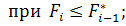
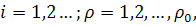
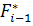 — минимальное значение функции качества за i —1 шагов поиска; Fi — значение функции качества на i - u шаге поиска; р— количество неудачных попыток, следующих друг за другом; ро — количество допустимых неудачных попыток,.следующих друг за другом;
— минимальное значение функции качества за i —1 шагов поиска; Fi — значение функции качества на i - u шаге поиска; р— количество неудачных попыток, следующих друг за другом; ро — количество допустимых неудачных попыток,.следующих друг за другом; 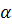 — вектор масштаба;
— вектор масштаба;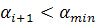 вычисления прекращаются.
вычисления прекращаются.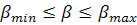 - область изменения параметров
- область изменения параметров 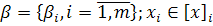 — ограничения на выходные переменные; F = F(
— ограничения на выходные переменные; F = F(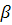 )— функция цели. Нужно найти такое
)— функция цели. Нужно найти такое 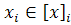 ,
, 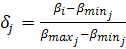 ;
; 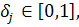
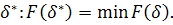
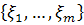 —случайный вектор, координаты которого равномерно распределены в интервале [0,1] и связана с ξ некоторым законом ξ= ξ(
—случайный вектор, координаты которого равномерно распределены в интервале [0,1] и связана с ξ некоторым законом ξ= ξ(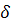 ). Использование обучения состоит в следующем: весь процесс поиска разбивается на m шагов, на каждом из которых производится
). Использование обучения состоит в следующем: весь процесс поиска разбивается на m шагов, на каждом из которых производится 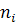 реализаций (i — номер шага).
реализаций (i — номер шага).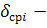 предполагаемое значение j-й координаты абсолютного min;
предполагаемое значение j-й координаты абсолютного min; 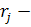 1/2 интервала, в котором поиск осуществляется с наибольшей интенсивностью;
1/2 интервала, в котором поиск осуществляется с наибольшей интенсивностью; 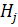 — интенсивность поиска в интервале;
— интенсивность поиска в интервале; 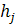 — интенсивность поиска в оставшейся области. На каждом шаге поиска, в зависимости от полученной информации, определяется
— интенсивность поиска в оставшейся области. На каждом шаге поиска, в зависимости от полученной информации, определяется 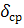 , 2r и Н. При этом, для каждой координаты
, 2r и Н. При этом, для каждой координаты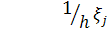 , если 0
, если 0 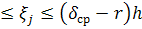
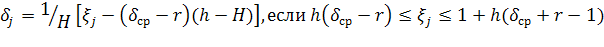
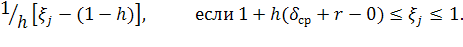
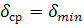 и min F(
и min F(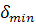 ).
).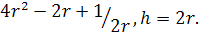 Причем, если
Причем, если 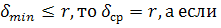
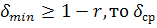 =1- r.
=1- r.


