
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выполнить оценку риска снятия плодородного слоя,
Когда фактическая толщина снятого верхнего слоя почвы меньше Проектной величины Проектное значение толщины снимаемого слоя почвы равно 45,5 см. Тип почвы - черноземы обыкновенные. Требуемый уровень надёжности РН =0,98. Следовательно, допустимый риск деградации почвы равен 0,02, а расчётный квантиль имеет значение u=2,050 (см. описание к формуле (1.14)). В табл.1.4 показаны результаты вычисления снятой толщины плодородного слоя в 38 точках, которые получены по данным нивелирования по квадратам, выполненного до и после снятия растительного слоя. Данные точки расположены в вершинах углов квадратов на всём участке отчуждения земель под строительство автомобильной дороги или другого инженерного сооружения (инженерные коммуникации, здания и промышленные сооружения). Формулы теории риска изменяются с изменением закона распределения исследуемого параметра (в данном случае исследуемый параметр – это толщины снятого плодородного слоя). Поэтому, для обоснования закона распределения данного параметра, выполним некоторые преобразования исходных данных, показанных в табл. 1.4. Начинают преобразовывать статистические данные с определения среднего значения и среднеквадратического отклонения толщин снимаемого плодородного слоя. Затем устанавливают на основе критерия Пирсона соответствие гистограммы распределения толщин плодородного слоя нормальному распределению, так как чаще всего данное распределение соответствует многим строительным параметрам и определяют риск деградации снимаемого слоя, в случае если параметры распределения толщин плодородного слоя не будут соответствовать проектным требованиям. Таблица 1.4 Толщина снятия плодородного слоя почвы (Н)
Статистическая обработка толщины снятия плодородного слоя почвы приведена в табл. 1.5. Примечание к расчету параметров в табл. 1.5. При применении мультипликативного метода и метода суммирования, измеренные значения толщин растительного слоя распределяют по разрядам (табл.1.5) в зависимости от частоты их появления в графе 3 «абсолютная частость». Вычисление данных графы 4 основывается на значениях графы 3. Первое значение переносится из графы 3 в графу 4, а затем к нему прибавляется второе значение из графы 3. Суммирование значений продолжают до последнего числа в графе 3. Контроль вычислений в графе 4 заключается в равенстве последнего числа этой графы и суммарного количества измеренных (или вычисленных) величин n. Данные графы 5 вычисляются так же, как данные графы 4 (по данным 4 графы). Контроль вычислений графы 5 подобен предыдущему контролю (см. табл. 1.5). Расчет среднего значения и среднеквадратического отклонения исследуемого параметра показан под табл. 1.5, с использованием её обозначений.
Таблица 1.5 Пример статистической обработки толщины снятия плодородного слоя почвы
Выполним обработку данных табл. 1.5 с использованием известных приемов математической статистики: Метод суммирования: - среднее значение:
- дисперсия:
- среднеквадратическое отклонение: Мультипликативный метод: - среднее значение:
- дисперсия:
- среднеквадратическое отклонение:
Сравнение эмпирического распределения с теоретическим законом распределения по критерию Пирсона показано в табл.1.6. Вероятность Pi в табл. 1.6 вычисляли по формуле Симпсона: В формуле (1.20) применяли параметр m =2. Тогда где b и a – правая и левая граница толщины снятия плодородного слоя почвы в разрядах интервалов (см. табл. 1.6);
 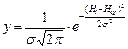 b (1.22) b (1.22)
где а – нижняя граница толщин в разряде интервалов (например, а=Н min=31см), а b – верхняя граница толщин в разряде интервалов (например, b=Н max=37см). Таблица 1.6 Сравнение фактического распределения толщин снятого плодородного слоя почвы с законом нормального распределения
При сравнении с нормальным законом распределения также применяли формулу вида (расчёт по формуле (1.23) значительно проще, чем по формуле (1.21), но даёт одинаковые (такие же) результаты):
где Ф(и) – функция Лапласа; Н i( min) и Н i+1( max) – левая и правая граница толщины снятия плодородного слоя почвы в разрядах (см. табл.1.6); Н cр и σН - средняя толщина снятия плодородного слоя почвы и среднеквадратическое отклонение толщины снятия плодородного слоя почвы. На рисунке 1.1 показано сравнение гистограммы (толщины снятия плодородного слоя почвы) с плотностью нормального распределения. Для теоретического распределения число степеней свободы определяли по формуле где k – число разрядов (в табл.1.6 k = 8); r – число наложенных связей (для нормального закона распределения r=3). Получаем ν =8-3=5. Из таблиц χ2 распределения (приложение 2) при χ2=5,0115 и ν=5 выписываем вероятность, по которой устанавливается соответствие теоретического закона распределения результатам измерений (гистограмме): - отличное соответствие при P >0,5; - хорошее соответствие при P =0,3÷0,5; - удовлетворительное соответствие при P =0,1÷0,3; - неудовлетворительное соответствие при P <0,1. Так как для приведенного выше примера P =0,43, то соответствие гистограммы (толщины снятия плодородного слоя почвы) плотности нормального распределения следует считать хорошим. Для сравнения теоретического и эмпирического распределения использовали также критерий Романовского Если критерий Романовского меньше 3, то гипотеза о соответствии фактической кривой распределения теоретическому закону распределения принимается. В противном случае при R≥3 делается вывод, что выбранный теоретический закон распределения не соответствует результатам измерения. Согласно этому критерию имеем
Так как 0,004<3, то нормальное распределение согласуется с результатами экспериментальных данных.
0,06
0,05 0,04 0,03 0,02
0,01 0 19 25 31 37 43 49 55 61 67, Н, см Рис. 1.1. Гистограмма толщины снятия плодородного слоя почвы и плотность нормального распределения
Учитывая, что
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.218.147 (0.016 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
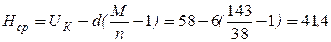 см;
см;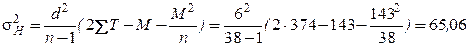 ;
;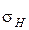 =8,07 см.
=8,07 см.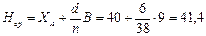 см;
см;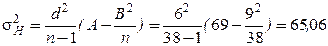 ;
;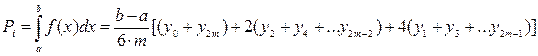 . (1.20)
. (1.20)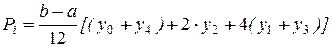 , (1.21)
, (1.21)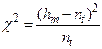
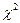 =5,0115
=5,0115
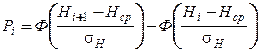 , (1.23)
, (1.23)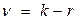 , (1.24)
, (1.24)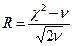 . (1.25)
. (1.25)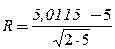 =0,004.
=0,004.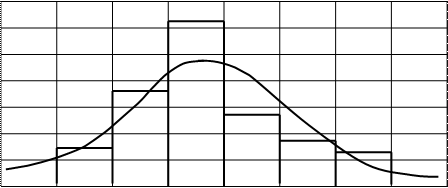 f(Н)
f(Н)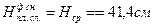 , а
, а 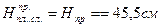 , то данному примеру соответствует математическая модель описанная неравенством
, то данному примеру соответствует математическая модель описанная неравенством 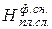 <
< 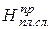 .
.


