
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка риска снятия плодородного слоя, когда фактическая толщина снятого верхнего слоя почвы меньше проектной величины
Когда фактическая толщина снятого верхнего слоя почвы меньше проектной величины ( где
u – квантиль подынтегральной функции, который математически зависит от требуемого уровня надёжности [1, 3] (и/или допустимой величины риска):
Приведём пример использования данных этой таблицы: при уровне надёжности РН = 0,90 получаем u = 1,283. И, следовательно, допустимая величина риска деградации плодородного слоя составит:
Параметры Среднеквадратическое отклонение где
При определении параметра Зависимость (1.16) справедлива потому, что фактические и критические параметры должны принадлежать к одной совокупности (то есть быть сопоставимыми, в данном случае по коэффициентам вариации). В противном случае необходимо обосновать – почему коэффициенты вариации критических параметров должны изменяться относительно коэффициентов вариации экспериментально установленных параметров (такое изменение коэффициентов вариации возможно только в том случае, когда при возникновении критических параметров появляется доминирующий фактор, например, меняется закон распределения). Значение критического параметра, когда При где
При Параметр где 0,05 – допустимое значение коэффициента вариации обоснованной в проекте расчётной (проектной) толщины почвенного слоя. Рассмотрим предложенную математическую модель для случая, когда Пример 1.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 60; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.005 с.) |
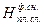 <
< 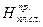 ), риск деградации оставшегося плодородного слоя на полосе отвода можно установить по зависимости, в которой требуется выполнение условия
), риск деградации оставшегося плодородного слоя на полосе отвода можно установить по зависимости, в которой требуется выполнение условия 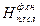 >
> 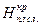 (то есть снятая толщина слоя должна быть всегда больше критической толщины):
(то есть снятая толщина слоя должна быть всегда больше критической толщины):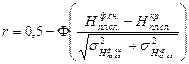 , (1.14)
, (1.14)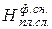 – фактическая снятая толщина плодородного слоя почвы, которая меньше требуемой (проектной) толщины и поэтому оставшаяся часть плодородного слоя подвержена погребению под земляным полотном автомобильной дороги или перемешена с разрабатываемым грунтом котлована (в обоих случаях эта часть плодородного слоя деградирует), см;
– фактическая снятая толщина плодородного слоя почвы, которая меньше требуемой (проектной) толщины и поэтому оставшаяся часть плодородного слоя подвержена погребению под земляным полотном автомобильной дороги или перемешена с разрабатываемым грунтом котлована (в обоих случаях эта часть плодородного слоя деградирует), см;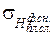 – среднеквадратическое отклонение фактической снятой толщины плодородного слоя почвы, см;
– среднеквадратическое отклонение фактической снятой толщины плодородного слоя почвы, см;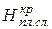 – критическая (минимальная) толщина снятого плодородного слоя почвы, при которой вероятность нежелательного последствия от утери части плодородного слоя или механического перемешивания с грунтом равна 50%, см (в случае, когда
– критическая (минимальная) толщина снятого плодородного слоя почвы, при которой вероятность нежелательного последствия от утери части плодородного слоя или механического перемешивания с грунтом равна 50%, см (в случае, когда 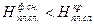 риск деградации оставшегося (не снятого) слоя стремится к единице);
риск деградации оставшегося (не снятого) слоя стремится к единице);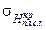 – среднеквадратическое отклонение критической толщины для снимаемого плодородного слоя почвы, см;
– среднеквадратическое отклонение критической толщины для снимаемого плодородного слоя почвы, см;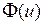 – функция Лапласа;
– функция Лапласа;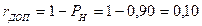 .
. 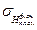 определяют в результате статистических расчетов по достаточному числу замеров толщины снятого плодородного слоя почвы (см. пример расчёта 1).
определяют в результате статистических расчетов по достаточному числу замеров толщины снятого плодородного слоя почвы (см. пример расчёта 1).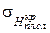 критической толщины снимаемого плодородного слоя почвы (
критической толщины снимаемого плодородного слоя почвы (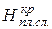 ) устанавливаются по зависимости:
) устанавливаются по зависимости: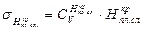 , (1.15)
, (1.15)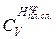 – коэффициент вариации минимальной (критической по минимуму) толщины снятого плодородного слоя почвы.
– коэффициент вариации минимальной (критической по минимуму) толщины снятого плодородного слоя почвы.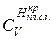 учитывают, что плодородный слой почвы при критической толщине снятия обладает той же однородностью исходных компонентов, что и при фактической толщине, т.е.:
учитывают, что плодородный слой почвы при критической толщине снятия обладает той же однородностью исходных компонентов, что и при фактической толщине, т.е.: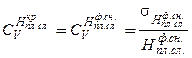 . (1.16)
. (1.16)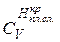 ≠ 1/u:
≠ 1/u: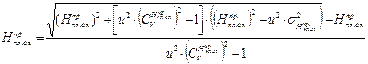 , (1.17)
, (1.17)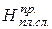 – проектная толщина снятия плодородного слоя, установленная в процессе изысканий (полевых работ) и проектирования, см;
– проектная толщина снятия плодородного слоя, установленная в процессе изысканий (полевых работ) и проектирования, см;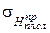 – допустимое среднеквадратическое отклонение проектной толщины снятия плодородного слоя, см.
– допустимое среднеквадратическое отклонение проектной толщины снятия плодородного слоя, см.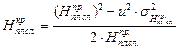 . (1.18)
. (1.18)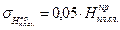 , (1.19)
, (1.19)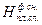 <
< 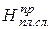 , на конкретном примере.
, на конкретном примере.


