
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критический анализ общей электродинамики
ВВЕДЕНИЕ Электрические и электродинамические явления приобретают в последнее время всё большее и большее значение. Они включают в себя оптику, законы излучения и многочисленные молекулярные явления, связанные с присутствием в веществе заряженных центров, ионов и электронов. Наконец, с появлением понятия электромагнитной массы, стало казаться, что уже и сама механика должна стать разделом общей электродинамики. Теория Максвелла в форме, приданной ей Г.A. Лоренцем, должна, таким образом, стать поворотным пунктом на пути к новой концепции природы, где законы электродинамики, рассматриваемые как первичные, содержали бы законы движения в качестве частных случаев и играли бы в физических теориях ту фундаментальную роль, которая до сих пор отводилась одной механике. Очевидно, что в этих условиях желательно иметь строгую критику основ этой теории, необходимой для придания последней большей степени ясности и точности, которой сама механика достигла лишь недавно и после многих споров. В порядке вещей задаться вопросом, какие гипотезы являются необходимыми и могут быть выведены из наблюдений, а какие являются логически бессмысленными или же могут быть отвергнуты без проверки их соответствия опытам, и, наконец, какие гипотезы могут и должны быть отклонены. Этим вопросом задаются в основном в отношении абсолютного движения. В первой части «Уроков по электричеству и оптике»1Пуанкаре посвятил некоторые исторические страницы критике более или менее различающихся теорий Максвелла и Герца. Поэтому нас будет интересовать только та форма теории, которую она приняла в руках Лоренца, форма, имеющая известные преимущества. Некоторые его выводы легко могут быть распространены и на другие теории. Здесь я лишь снова напомню или завершу идеи, выдвинутые Пуанкаре, и более важные – Лоренцем, который хорошо видел различные аспекты, в свете которых могла интерпретироваться его теория. В целом, я выделил явления молекулярного порядка, задаваемые в рамках корпускулярной теории электричества. Очевидно, эта плодотворная концепция по большей части не зависит от тех идей, к которым мы можем прийти, исходя из принципа воздействия электрических зарядов друг на друга через эфирную среду, представляющую собой наиболее специфичный объект электродинамических уравнений.
Результат этих исследований окажется неблагоприятным для существующих теорий. Дискуссии о трудностях, которые они порождают, показывают, что трудности эти имеют общее происхождение, тесно связанное с понятием эфира, который является основой всех этих теорий. Конкретнее, мы увидим что: 1. С точки зрения строгой логики электрические и магнитные силы, внешне играющие в теории столь фундаментальную роль, являются понятиями, которые мы можем полностью устранить. В действительности они представляют собой лишь соотношения пространства и времени. Тем самым мы возвращаемся к прежним представлениям об элементарных воздействиях, с той лишь разницей, что они уже не считаются мгновенными. 2. Теория [Максвелла-Лоренца] допускает бесконечное число решений, удовлетворяющих всем условиям, но несовместимых с опытом и даже, например, приводящих к вечному движению. Чтобы исключить эти решения, мы вынуждены будем принять в качестве гипотезы формулы для запаздывающих потенциалов. Эти формулы вводят в электродинамику необратимость, тогда как общие уравнения электродинамики допускают обратное течение процессов. Я показываю, вопреки принятым воззрениям, что эти уравнения не могут быть выведены из соответствующих параметров начального состояния. Они составляют новую гипотезу, делающую ненужными уравнения электродинамики в частных производных. Чтобы пояснить эту гипотезу, достаточно ввести элементарные воздействия, для чего надо отказаться от основополагающей идеи Максвелла об их отклонении. 3. Понятие локализации энергии в эфире неопределённо и допускает множество простых решений. 4. Максвелл показал, что гравитацию нельзя свести к тем же понятиям [поля, эфира – Сергей Семиков ]. Тот факт, что введение отрицательной энергии привело бы к неустойчивой системе, показывает: эти понятия [поле, эфир] не имеют универсальной применимости к силам природы. 5. Действие и противодействие не равны, и это их неравенство в том виде, в каком оно следует из введения абсолютных скоростей, противоречит эксперименту.
6. Эксперименты Кауфмана по электрическому и магнитному отклонению бета-лучей, испускаемых радием, ещё не доказывают, что масса электронов имеет полностью электромагнитное происхождение и зависит от их абсолютной скорости. Ведь с одной стороны, ничто не обязывает нас верить, что силы представляют собой, как в теории Лоренца, линейные функции скорости (это может быть верно лишь при малых скоростях), и что, с другой стороны, один из экспериментов Троутона и Нобля показывает, что выражение для электромагнитного импульса как функции скорости, из которой Абрагам вывел формулу электромагнитной массы, определено неточно. 7. Теория Максвелла и Лоренца начинается с введения системы абсолютных (то есть независимых от любых движений вещества) координат. Но чтобы было согласие с экспериментом, который всегда – и в оптике, и в электродинамике, также как и в механике, – подтверждает принцип относительности движения, мы должны отвергнуть эту абсолютную систему как гипотезу, имеющую весьма малую вероятность, раз устраняются понятия твёрдых тел и постоянства массы. Пришлось бы также изменить принципы кинематики, рассматривая правило параллелограмма скоростей исключительно как первое приближение, имеющее силу лишь при малых скоростях, а время и одновременность сделав целиком относительными понятиями. Для экономии нашего мышления было бы весьма прискорбно, если б мы были вынуждены жить со всеми вышеперечисленными осложнениями. Я думаю, что вместо прежней кинематики должна быть устранена гипотеза эфира, а с ней и представление явлений уравнениями в частных производных. Необъяснимость того, почему тела не встречают никакого сопротивления в эфире, когда проходят сквозь него, и того факта, что они не изменяют его состояния, а также множество других соображений приводят к простому физическому пространству вне механического френелевского эфира, предельно проницаемого для вещества, и вне системы абсолютных координат. В настоящее время эфир – это не более чем математическая абстракция, и его устранение было бы лишь заключительной стадией продолжительного развития. Этот вывод, как я покажу позднее, отнюдь не связан с возвращением к действию на расстоянии [дальнодействию – С.С. ]. Но он, и впрямь сталкивается "в лоб" со многими принятыми в настоящее время идеями, и я первый готов признать, что гипотеза, сослужившая столь большую службу Науке, не может быть осуждена по той только причине, что ныне она создаёт некоторые, по-видимому, серьёзные трудности. Мы всегда должны надеяться на дальнейшее разрешение этих трудностей, или признать, что они являются неотъемлемой частью вещей, и не зависят от наших моделей. К счастью, причина не в этом. Это я стремился показать в ЧАСТИ ВТОРОЙ этой работы. Но теория, которую я буду там представлять, не претендует на то, чтобы стать удовлетворительным и определённым решением столь сложной проблемы. Её первоочередная задача состоит в том, чтобы показать, насколько велика та часть неизвестного, которая, несмотря на недавний прогресс, всё ещё имеется в данной области, и насколько [она] превосходит объём того, в чём мы хотели бы быть твёрдо уверены. Экспериментальные свидетельства можно рассматривать как подтверждение теории Максвелла и Лоренца, приняв даже, как это сделаю я, замечательные идеи этого последнего в отношении атомного строения электричества, природы тока проводимости и диэлектриков, одним словом, электронную теорию. Из этого АНАЛИЗА станет видно, что не обязательно вводить абсолютное движение, ставя тем самым с ног на голову кинематику и понятие времени: было бы вполне достаточно одних относительных скоростей. Здесь будут использоваться не те понятия, что подвергаются критике, такие как поляризация, электрический вектор, магнитная сила, и т.п., но лишь понятия времени, пространства и электрических зарядов. Только эти последние играют, подобно массам в механике, роль удобных коэффициентов, постоянных для заданного тела или электрона. В некотором смысле это будет механическая теория электричества. Однако я сомневаюсь, что надо вводить более или менее сложные скрытые механизмы, играющие столь важную роль в теории Максвелла. Такие гипотезы не являются ни обязательными, ни, как можно заметить, вполне удовлетворительными. Действительно, достаточно вспомнить, что весомые тела должны проходить сквозь эти сложные механизмы, не нарушая их и не воспринимая ощутимого воздействия, даже когда их скорость достигает скорости небесных тел. В частности, непроницаемость отсутствует в механических теориях [эфира], и это один из моментов, который не всегда вполне укладывается в доказательство. Опыт показал, что воздействия не мгновенны, также он не выявил хоть какого-то следа среды, могущей существовать в свободном от вещества пустом пространстве. Поэтому я посчитал, что могу ограничить себя тем, что дам закону распространения этих воздействий очень простое кинематическое истолкование, заимствованное из теории истечения света и удовлетворяющее принципу относительности движения. Фиктивные частицы постоянно испускаются во всех направлениях электрическими зарядами. Они продолжают неограниченно распространяться вдоль прямых линий с постоянной скоростью, даже при движении сквозь материальные тела. Воздействие, оказываемое на заряд, зависит лишь от расположения, скорости, и других параметров этих частиц в его непосредственной близости. Частицы, таким образом, – это всего лишь конкретное представление кинематических и геометрических параметров. Эти гипотезы достаточны для чисто критической цели, которой я здесь задался. Они позволяют подробно исследовать закон элементарных взаимодействий между движущимися электронами и в частности показать, что этот закон, практически совсем неизученный для больших скоростей, требует даже на небольших скоростях введения неопределённого параметра k, отчасти аналогичного тому, что ввёл в своей теории Гельмгольц.
Нам придётся проанализировать временные возможности этих гипотез. Действительно, когда частицы (или, если угодно, элементарные воздействия, сгустки энергии), испущенные заряженным телом, достигают другого электрического заряда и изменяют его движение, принцип действия и противодействия требует, чтобы они стали его частью, отклонились или трансформировались. И весьма примечательно, что эксперимент Физо по увлечению [световых] волн, как и другие известные факты оптики, не совместим с допущенной здесь гипотезой, и требует подобной реакции. Это полная противоположность тому, что происходит по гипотезе эфира, как представлял его Пуанкаре. Теория Герца, которая удовлетворяет принципу действия и противодействия, является несовместимой с экспериментом Физо, теория же Лоренца этому принципу не удовлетворяет, зато полностью объясняет эксперимент. Но Пуанкаре показал, что, придав лучистой энергии импульс, всё можно поставить на свои места. Очевидно, что такое предположение вполне естественно, если эта энергия излучается, испускается, а не распространяется [в среде]. Только такое допущение позволяет сохранить этот принцип в новой модели, предложенной мною. Мы можем даже предвидеть, что, исходя из этих принципов, получится вывести электродинамические члены, зависящие от скорости и ускорения, руководствуясь одним лишь соображением распространения [излучения?]. Именно эту проблему Гаусс поставил в своём известном послании к В. Веберу, и которую теория Максвелла не решила, поскольку ввела для этих членов особую величину, векторный потенциал. Я вернусь к этим вопросам позднее. Предшествующие замечания вполне объясняют, почему я не обращался к оптике в этом критическом анализе. Таким образом, новая теория во многом возвращает нас к некоторым ещё более древним классическим идеям, которые, казалось бы, будут безвозвратно забыты. Неизбежно, что при этом истолкование некоторых экспериментов изменится. В частности, может оказаться и так, что часть или вся масса имеет электромагнитное происхождение, однако она будет постоянной и не зависимой от абсолютной скорости. Меняется не масса, но сила. Эксперименты Кауфмана вполне допускают и эту новую точку зрения. Новые формулы применимы к тяготению, они позволяют устранить, по крайней мере, в значительной части, наиболее очевидное расхождение, имеющееся в настоящее время между вычислением и экспериментом в отношении векового смещения перигелия Меркурия. Электронная теория представляет собой первый частичный возврат от идей Максвелла к другим, намного более древним. И тот, кто считает необходимым дальнейшее развитие в том же ключе гипотез Лоренца, оказавшихся столь плодотворными, поддержит их важность, и математическую форму, которую он им придал, и которая в большинстве случаев остаётся наиболее изящной и практичной.
ЧАСТЬ ПЕРВАЯ ОБРАЩЕНИЕ К ТЕОРИИ ЛОРЕНЦА1 Известно, что Максвелл не выдвигал гипотез о природе электрических токов. Лоренц утверждал, что полный ток проводимости является результатом движения электрических частиц, подвергнутых действию своего рода трения в проводниках и упругих сил в диэлектриках. Многочисленные эксперименты последних лет подтвердили эту гипотезу. Эта концепция позволила Лоренцу в его фундаментальных уравнениях рассматривать только диэлектрический эфир. Отказавшись от чисто механического объяснения и от непроницаемости вещества, Лоренц считает эфир неподвижным и присутствующим даже внутри ионов и электронов. Ионы и электроны физически изменяют его, и это изменение, которое сложно описать конкретно, характеризуется двумя векторами: электрическим, или вектором электрического смещения диэлектрика E, компоненты которого - Ex, Ey, Ez, и магнитным вектором H (Hx, Hy, Hz). Электрические заряды находятся в ионах, которые считаются жёсткими. Если ρ – это электрическая плотность, измеренная в электростатических единицах в точке (x,y,z) в момент t (система координат связана с неподвижным эфиром), v - скорость электрически заряженного вещества в координатах (x, y, z, t), а c - скорость света, то
Таким образом, поле, создаваемое в эфире другими зарядами, воздействует на элементарный заряд ρ dτ с механической силой, заданной по величине и направлению вектором F ρ dτ, где
В этой теории магнетизм не имеет места:* магнитное воздействие создают амперовы молекулярные токи. При помощи некоторых гипотез, к которым мы ещё вернёмся, эта система уравнений может быть составлена посредством введения запаздывающих потенциалов. Фактически, мы показываем, что все решения системы уравнений с (I) по (V), где приняты значения ρ, Vx, Vy, Vz, могут быть выражены в виде
где функции Φ (скалярный потенциал) и Ax, Ay, Az (компоненты векторного потенциала) непрерывны вместе со своими первыми производными во всём пространстве, от нуля до бесконечности, и удовлетворяют уравнениям
и
У Лоренца эти условия выполняются, посредством принятия
Эти выражения имеют вид ньютоновских потенциалов, с той лишь разницей, что вместо величины ρ в точке (x', y', z') в момент t, мы будем брать её значение в предшествующий момент t'= t- r/c: время r/c необходимо для распространения. И то, в чём мы расходимся с Лоренцем, даётся выражениями
Следовательно, поле полностью определено, и подставляя выражения (XII) и (XIII) в формулы (VII), (VIII) и (VI), мы получаем для Fx
и аналогичные выражения для Fy и Fz. Вводя полную производную
и устанавливая
Шварцшильд2 нашёл для Fx замечательную формулу
Такой вид имеют уравнения Лагранжа. Выражения (XIV) и (XVI) дают силу, которая приложена к электрической точке единичного заряда, выраженную посредством элементарных воздействий, аналогичных тем, что рассматривались в прежней электродинамике, не учитывающей конечную скорость передачи, которую мы снова находим у Гаусса и К. Неймана. Заряд e', который считаем точечным, воздействует, исходя из самых общих соображений, на другой заряд e с силой
где
Эти выражения в первом приближении сводятся к закону [обратного] квадрата расстояния. Поэтому мы можем называть их обобщённым законом Ньютона. Его точное выражение будет дано позднее. В этих формулах понятие поля не играет роли. Весьма примечательно, что Клазиус, как и Вебер, в поиске объяснения электродинамическим воздействиям через действие на расстоянии в зависимости от положений, скоростей и ускорений заряженных точек, получил те же формулы (XV) и (XVI), с той только разницей, что считал воздействия мгновенными, то есть брал величины ρ' и v' в момент времени t, а не в t–r/c. Этот весьма примечательный вывод, которым мы обязаны Шварцшильду, показывает, что теория Лоренца очень близка к прежним теориям. Первоначальный вид, который Лоренц придал своей теории, был менее абстрактным в том смысле, что, следуя путём, с которого свернул Максвелл, он исходил из уравнений Лагранжа, введя два типа переменных: первые определяли положения заряженных частиц, а вторые – состояние эфира. Мы присваиваем этим последним одну лишь кинетическую энергию, без учёта её внутренних перемещений. Впрочем, это не отменяет того, что они существуют. Аналогично принцип Гамильтона позволяет, ограничивая изменения при некоторых условиях, получить фундаментальные уравнения с (I) по (VI), рассматривая электрическую энергию...
как потенциальную, а магнитную энергию
как кинетическую.3 Этот вывод весьма непрост и может быть сделан в разных формах.[4] Эти два аспекта теории Лоренца заметно различаются. Второй аналогичен теории Лармора,[5] которая, приводя к тем же самым формулам, предлагает конкретные гипотезы о движении эфира в электромагнитном поле, заимствованные у концепции гиростатического эфира лорда Кельвина. Эфир несжимаем и движется в направлении магнитных силовых линий. Известно, что Максвелл и Герц объясняли механические силы, испытываемые веществом в электромагнитном поле, давлением, которое эфир, как предполагается, оказывает на вещество, и наоборот: во всех случаях действие одного равно и противоположно направлено реакции другого. Эти давления, как показал Гельмгольц,[6] стремятся сохранить простой эфир (предположительно несжимаемый) в движении. В единице объёма они пропорциональны производной по времени от вектора Пойнтинга S:
Лоренц рассматривает эфир как неподвижный. Таким образом, он склоняется к максвелловской теории давлений, и отсюда следует равенство действия и реакции. Не скомпенсированная сила характеризуется вектором
В заключение этого краткого представления, заметим, что, если мы допускаем неизвестные движения в эфире, то решение уравнений существует только для значений близких по порядку величины к отношению скорости эфира к скорости света. §2. - КРИТИКА ПОНЯТИЙ ЭЛЕКТРИЧЕСКОГО И МАГНИТНОГО ПОЛЕЙ * Известно, что введение понятия силы в механику было предметом больших споров. Это понятие апеллирует к мышечному ощущению, тогда как представления о пространстве и времени имеют в основном осязательное и визуальное происхождение. Эта непреодолимая психологическая двойственность, введённая в самую основу этой фундаментальной науки, оставляет в разуме чувство некоторого дискомфорта, оправдываемое тем кажущимся вполне очевидным обстоятельством, что понятие в каждом конкретном случае самоустраняется. Измеряем ли мы силы массами и ускорениями, или же электрическими деформациями, сопоставляем ли мы эти эффекты с эффектами тяготения, и т.д., но то, что мы наблюдаем и измеряем в действительности, – это смещение, или же отсутствие его. Опять же, в этом последнем случае, мы лишь перестаём обнаруживать разницу двух сил. В уравнениях механики, применённых к любому частному случаю, остаются исключительно отношения пространства и времени, с некоторыми коэффициентами (соответствующим образом выбранными и неизменными), представляющими собой массы или другие физические постоянные. Поэтому многие эксперты с позиций чистой логики и на серьёзном основании исключали понятие силы из фундаментальных уравнений как бесполезное. Современная электродинамика целиком основана на понятии электрических и магнитных сил. Было бы прискорбно, если б они были абсолютно необходимы. Но, к счастью, это не так: в уравнениях эти понятия самоустраняются, они логически бесполезны. В окончательном анализе теория выражает только существование некоторых пространственно-временных отношений, как это имеет место в механике. Поэтому желательно выводить эти отношения непосредственно. Тем самым мы вернёмся к классическим элементарным воздействиям. Какими же должны быть в действительности точные определения векторов полей E и H? Я утверждаю, что определения этих векторов вытекают непосредственно из теории. Так, не зная значения этих символов, мы можем сразу, при помощи некоторых гипотез, которые проанализируем в следующем разделе, проинтегрировать фундаментальные уравнения, используя метод запаздывающих потенциалов, и тогда получим в итоге выражения (XIV) и (XVI). Уравнения движения для материальной точки с зарядом e, массой m и координатами x, y, z будут
После замены Fx,... значением из (XIV) или (XVI) (члены будут играть особую роль лишь в отношении электрона), мы будем иметь в (1) и (2) только пространственно-временные отношения, даже при условии Теперь я утверждаю, что уравнения Лоренца в действительности не выражают ничего кроме (1) и (2). Это значит, что поле совершенно не играет роли в чистом эфире. Фактически, мы можем определить лишь величину и направление поля, когда помещаем в него тело и наблюдаем механические силы, воспринимаемые им, или когда ограничиваемся наблюдением его движений и движений ионов возле него, движений, которые проявляются в свечении, тепловых, химических и других явлениях. Таким образом, единственное, что мы узнаём – это F, да и то только в точках Необходимо пояснить смысл этого утверждения. Скажем, в теории света, всё что по теории Лоренца представляется подобным образом [через поля], может быть получено и через элементарные воздействия между ионами источника света, ионами диэлектриков или проводников, создающими оптическое изображение, и, наконец, ионами сетчатки или фотопластинки, на которой получается отпечаток. Так, мы привыкли описывать явления дифракции, наблюдаемые в случае со щелью и экраном, рассматривая вместе с Френелем точки эфира в щели как множество центров волнообразования. Это противоречит уравнению запаздывающих потенциалов. Единственные места зарождения волн – это электрические заряды. Теория Лоренца или закон элементарных воздействий, объяснили бы эти явления совместным воздействием ионов источника и экрана. К тому же, легко показать, используя принцип Гюйгенса, как это делает Кирхгоф, эквивалентность этих двух методов и в отношении результатов. Это уже не позволяет утверждать, что поле – это чисто математическое промежуточное звено, без которого мы могли бы обойтись, если б имелась возможность обнаружить его присутствие в эфирном пространстве, не помещая для этого в него какое-нибудь тело. Это произошло бы, например, в том случае, если бы эфир под влиянием поля становился восприимчив к изменениям, или был способен хоть сколько-то смещаться, как того хочет Герц, и как требует лорд Кельвин.1 Интерференционные эксперименты могли бы в подтверждение выявить скорость эфира. Вообще говоря, такие идеи были весьма широко распространены, однако, как известно, эксперимент, проведённый несколько раз,2 дал лишь отрицательные результаты, также, как и все прочие эксперименты, поставленные с целью доказать существование эфира. С другой стороны, предположение всех этих движений не дало хоть сколько-нибудь вероятного механического объяснения электрическим воздействиям в электрических же явлениях. Поэтому Лоренц в последних вариантах своей теории попытался его исключить. И именно это служит для нас сигналом к упразднению понятия силы и поля в этой теории, что не затрагивает никаких фактов действительности или какого-либо возможного эксперимента, соответствующего ей. Лоренц уже высказал3 эту точку зрения: "Таким образом, мы видим, что в новом способе, которым я собираюсь представить теорию Максвелла, она сближается со старыми идеями. Мы сможем даже, после того, как найдём простые формулы, описывающие движения частиц, не принимать во внимание рассуждение, их породившее, и рассматривать эти формулы как выражение фундаментального закона, близкого к законам Вебера и Клазиуса". Однако воздействия уже не мгновенны, и с учётом этого важного ограничения мы видели, что имеется даже идентичность с законом Клазиуса. Легко видеть, что понятие поля вводит понятие абсолютного движения, коль скоро скорости играют роль в выражении для поля или в выражении для его воздействия на тела. Отныне они зависят уже не от одних лишь координат и ускорений. §3. - НЕОБРАТИМОСТЬ И ЗАПАЗДЫВАЮЩИЕ ПОТЕНЦИАЛЫ * Изучим теперь подробней гипотезу, связывающую дифференциальные уравнения (IX) и (X) с формулами запаздывающих потенциалов (XII) и (XIII) и покажем, что первые легко преобразуются во вторые, тогда как обратное преобразование невозможно. Но сначала нам придётся уяснить физический смысл формул. В противоположность механическим, электромагнитные явления в целом необратимы за счёт излучения. Учитывая это, мы можем даже надеяться получить с их помощью более полное истолкование необратимых физических явлений. Но уравнения Лоренца не изменятся, если мы поменяем направление течения времени. Они содержат понятие обратимости, тогда как для запаздывающих потенциалов и элементарных воздействий прямое и обратное направления хода времени играют совершенно разные роли. Как в необратимых циклах Гельмгольца, мы вводим скорость, предположительно не способную изменять своё значение, скорость, с которой волны всегда только расходятся от породивших их тел. Именно отсюда следует электромагнитная необратимость. Таким образом, эта предварительно принятая дополнительная гипотеза должна быть тщательно изучена. Для непрерывной функции f(x, y, z, t), пропорциональной электрической плотности в точке (x, y, z, t), и функции φ, имеющей непрерывный потенциал во всём пространстве, вплоть до бесконечности, и всегда удовлетворяющей уравнению
легко проверить, что интеграл
является решением уравнения (3). Действительно, вырежем малый объём τ0 возле точки (x, y, z) и продифференцируем подынтегральное выражение по той части пространства, в которую не входит точка (x, y, z). Применяя операцию
Операция Δ, применяемая к первому члену, даёт в соответствии с теоремой Пуассона Мы показываем, что
или, более обще,
являются решениями (3), при условии, что произвольные функции F 1 и F 2 удовлетворяют отношению
Решение φ1 соответствует волнам, расходящимся во всех направлениях от породивших их электрических зарядов. Решение φ2 соответствует волнам, пришедшим из бесконечности и сходящимся к тем же самым точкам. В отличие от решения φ1, которое зависит только от предшествующих состояний, φ2 определяется последующими. Решение φ3 включает оба вида волн. И наконец, φ4 соответствует волнам, центры образования которых могут находиться в свободном [от вещества] эфире, где f = 0. Опыт показывает, а Лоренц признаёт, что существовать могут только волны типа φ1, и кроме того, мы увидим, что обратные гипотезы повлекли бы недопустимые следствия, наподобие возможности вечного движения. Для начала мы делаем вывод, что уравнения Лоренца (этот вывод также распространяется на уравнения Максвелла и Герца) допускают бесконечное число решений, удовлетворяющих всем условиям, но несовместимых с экспериментом. Мы легко находим такие решения, и приходим к выводу, что их необходимо a priori игнорировать всякий раз, когда мы рассчитываем, скажем, электрические колебания системы (проводящей сферы, генератора Герца, колеблющегося электрона, и т.д.). Обсудим гипотезу, согласно которой мы сочли, что можно устранить эти решения. Мы показываем, что для всех решений (3) внутри замкнутой поверхности S
где мы приняли, как и прежде,
Предположим, что в любой момент t =0, находящийся в прошлом, мы имели всюду, или, по крайней мере, на больших расстояниях,
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.137.64 (0.096 с.) |
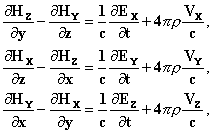 [1-е уравнение Максвелла]
[1-е уравнение Максвелла]
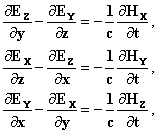 [2-е уравнение Максвелла]
[2-е уравнение Максвелла]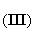
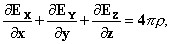 [3-е уравнение Максвелла]
[3-е уравнение Максвелла]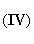
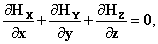 [4-е уравнение Максвелла]
[4-е уравнение Максвелла]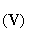
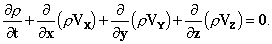 [закон сохранения заряда]
[закон сохранения заряда]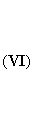
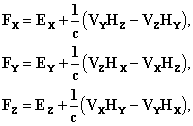
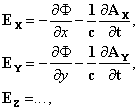
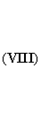
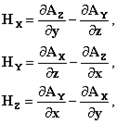
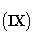
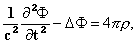
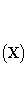
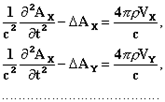
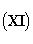
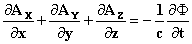
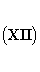
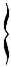
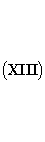
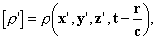
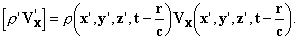
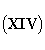
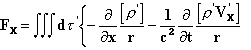
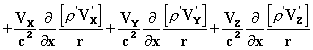
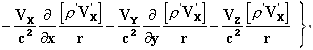
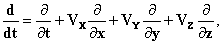
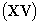
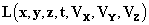
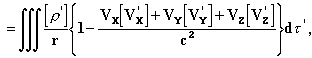
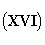
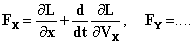
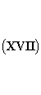
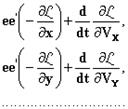
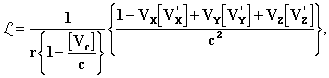
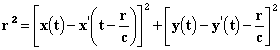
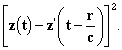
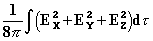
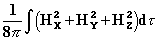
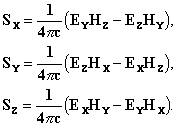
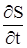 .[7]
.[7]
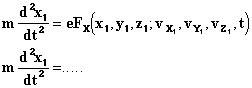
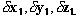 Если мы захотим принять во внимание воздействие электрона самого на себя или его связи, то придётся применить принцип Даламбера. Тогда получим, распространяя интегрирование по всему электрону и обозначая через виртуальные перемещения, допускаемые связями, а через
Если мы захотим принять во внимание воздействие электрона самого на себя или его связи, то придётся применить принцип Даламбера. Тогда получим, распространяя интегрирование по всему электрону и обозначая через виртуальные перемещения, допускаемые связями, а через 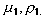 плотности вещества и электрического заряда,
плотности вещества и электрического заряда,
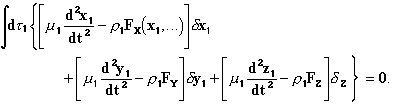
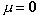 , то есть, в случае если масса имеет полностью электромагнитное происхождение.
, то есть, в случае если масса имеет полностью электромагнитное происхождение.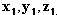 , где есть заряженное вещество, и потому находим E и H лишь из рассуждения (которое не всегда столь уж очевидно в случаях, где требуется рассмотреть абсолютное движение). Это говорит о том, что во всех случаях для нахождения формулы, задающей F как результат элементарных воздействий, оказываемых элементарным зарядом на другой элементарный заряд, это второе представление в свете фактов является точным эквивалентом первого, основанного на поле и его уравнениях в частных производных, которые играют чисто математическую роль. Если пожелаем, мы можем вовсе обойтись без понятий электрического и магнитного поля.
, где есть заряженное вещество, и потому находим E и H лишь из рассуждения (которое не всегда столь уж очевидно в случаях, где требуется рассмотреть абсолютное движение). Это говорит о том, что во всех случаях для нахождения формулы, задающей F как результат элементарных воздействий, оказываемых элементарным зарядом на другой элементарный заряд, это второе представление в свете фактов является точным эквивалентом первого, основанного на поле и его уравнениях в частных производных, которые играют чисто математическую роль. Если пожелаем, мы можем вовсе обойтись без понятий электрического и магнитного поля.
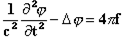
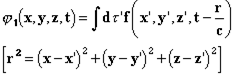



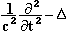 , получаем ноль. Внутри объёма τ0 снова произведём операцию
, получаем ноль. Внутри объёма τ0 снова произведём операцию 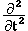 , дающую под знаком интеграла результат, стремящийся к нулю, как и τ0. Чтобы произвести операцию Δ, внесём r, являющееся малым, в τ0.
, дающую под знаком интеграла результат, стремящийся к нулю, как и τ0. Чтобы произвести операцию Δ, внесём r, являющееся малым, в τ0.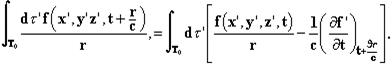
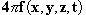 . Во втором члене знаменатель r отсутствует. Результат вместе с τ0 сокращается до нуля. Таким образом, мы получаем уравнение (3). Я не настаиваю категорично на условии непрерывности, гарантирующем, что производные от f существуют.
. Во втором члене знаменатель r отсутствует. Результат вместе с τ0 сокращается до нуля. Таким образом, мы получаем уравнение (3). Я не настаиваю категорично на условии непрерывности, гарантирующем, что производные от f существуют.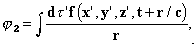
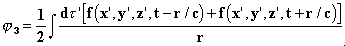
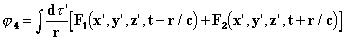
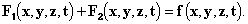
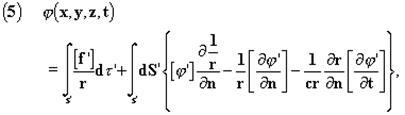
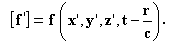
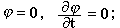 мы могли бы для всех положительных значений t и во всех точках (x, y, z) выбрать в качестве S сферу с центром (x, y, z) и радиусом R > ct достаточно большим, чтобы все члены поверхностного интеграла были нулевыми. Тогда формула (4) сохранится. Эти рассуждения требуют следующих замечаний:
мы могли бы для всех положительных значений t и во всех точках (x, y, z) выбрать в качестве S сферу с центром (x, y, z) и радиусом R > ct достаточно большим, чтобы все члены поверхностного интеграла были нулевыми. Тогда формула (4) сохранится. Эти рассуждения требуют следующих замечаний:


