
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Организация поточного производства
Например, для изготовления некоторого электронного блока на конвейерной линии нужно проделать определенное количество операций по монтажу и пайке элементов — элементарных опера- ций. Каждая из этих операций имеет определенное время выпол- нения. Число операций с некоторым заданным временем выпол- нения также определено. Элементарные операции выполняются исполнителями — монтажниками или роботами на закрепленных за каждым из них рабочих местах. Один монтажник или робот вы- полняет несколько элементарных операций, причем суммарное время выполнения всех операций на одном рабочем месте не должно быть больше некоторого времени, называемого ритмом конвейера. Задача синхронизации конвейерной линии состоит в таком распределении операций по рабочим местам, при котором суммарное время выполнения всех элементарных операций на каждом рабочем месте будет не больше ритма, при условии, что будут распределены по рабочим местам все операции, необходи- мые для изготовления данного блока. При этом суммарные потери времени на конвейерной линии должны быть минимальными. Кроме того, для учета других критериев при организации кон- вейерной линии необходимо получить различные варианты реше- ния задачи синхронизации. Для удобства дальнейшего изложения введем некоторые обо- значения и определения: 1) обозначим время выполнения элементарной операции t j (j = 1, n), где n — число элементарных операций с разным временем выполнения; 2) элементарную операцию с временем t j будем называть j м элементом или элементом j; 3) число элементарных операций с временем t j назовем ресур- сом элемента j и обозначим w j; 4) число рабочих мест обозначим буквой m, а ритм — r; 5) число элементов j на рабочем месте с номером i обозначим как x ij. Совокупность их запишем в виде матрицы, которую назовем элементной матрицей. Теперь индексы i и j будут означать, что x ij находится в i й строке и j м столбце. Таким образом, каждому ра- бочему месту соответствует одна строка. Поэтому дальше между рабочими местами и соответствующими им строками различия делаться не будут; 6) наконец, обозначим разность между ритмом и временем вы- полнения всех элементарных операций на i м рабочем месте D t i, т.е.
n D t i = r - å x ij ´ t j. j =1
Эту разность будем называть рассинхронизацией на i м рабочем месте. Совокупность всех величин D t i представим в виде векторастолбца, который будем называть столбцом рассинхрони- зации. Уже сейчас можно наложить некоторые ограничения на обоз- наченные выше величины: x ij и D t i, так же, как w j, t j и r, являются целыми и неотрицательными. Объясняется это тем, что элемен- тарная операция не может делиться на части, т.е. на рабочем месте может выполняться только целое число операций. Действительные времена t j могут выражаться нецелым числом секунд или минут, но 2 5 детерминированные t j измеряются целым числом секунд; r — целое как сумма целых; D t i — целое как разность целых S x ij t j и r и неот- рицательное, так как
n r ³ å x ij ´ t j. j =1
Математически задачу синхронизации конвейерной линии можно сформулировать следующим образом. Даны два конечных множества натуральных чисел
причем t j «w j, т.е. между элементами этих множеств суще- ствует взаимнооднозначное соответствие. Задано также некоторое m Î N (число рабочих мест). Необходимо найти целочисленную функцию r (d) = min r (d) — dÎ Z ритм конвейерной линии, удовлетворяющий системе
ïå x ij ´ t j £ r, i = 1, m; ï j =1
í m ïå x ij =w j,
j = 1, n, где x ij Î Z (эти числа отыскиваются в процессе решения зада- чи). Заметим, что для функции r (d) должны выполняться следующие неравенства:
n 1) r ´ m ³ åw j ´ t j, j =1 так как в правой части неравенства стоит сумма, означающая полное необходимое время для выполнения всех элементарных операций; 2) r (d) ³ m ax t j, j =1, n так как мы ранее предположили, что все x ij Î Z (т.е. элементар- ная операция не может делиться на части). Исходя из замечания 1 зададим начальное значение функции r (d) в следующем виде: é n w ´ ù êå j t j ú r (d) = ê j = 1 ú + d, нач êë m úû где d = d (w1, …, w n; t 1, …, t n; m) является неявной функцией указанных переменных, причем
ï åw j
´ t j
ï ï ï ï0, если î j = 1 Ï Z ; m n åw j ´ t j j = 1 Î Z . m Также исходя из замечания 2 проверим r (d) ³ max t j, и если это условие не выполняется, то предполагается, что r (d) = m ax t j. j =1, n Практически задачу синхронизации можно рассматривать как задачу решения следующей системы:
ï j =1 í m ïå x
= w,
j = 1, n. (1) ï î i =1 ij j Далее рассматривается один из специальных приемов — эврис- тический метод решения системы (1). Суть его заключается в сле- дующем: пытаться найти x ij, удовлетворяющие неравенствам: n
å xij ´ t j £ r, i = 1, m, j =1
(2) причем так, чтобы x ij были неотрицательными и целыми для всех возможных i, j и чтобы выполнялись условия:
m å xij £ w j, i =1 j = 1, n. (3) Этот процесс будет составлять только часть всего алгоритма ре- шения задачи. Назовем его фазой 1. Если в результате распределе- ния элементарных операций по рабочим местам на первой фазе часть элементарных операций остается нераспределенной, то это означает, что первая фаза не приводит к решению задачи. В этом случае необходимо применить другую часть алгоритма — фазу 2, которая будет заключаться в попытке распределить оставшиеся элементарные операции по сформированным рабочим местам. Если эта попытка будет также неудачной, то ритм конвейерной линии должен быть увеличен на 1 и процесс решения повторяется с фазы 1. Это основная идея алгоритма для решения системы (1). Блоксхема обобщенного алгоритма приведена на рис. 11.3.
методические рекомендации по расчету показателей поточно-конвейерных линий (ПкЛ) Расчет программы запуска (N з) производится по формуле
з 100 - a где N в — программа выпуска готовых изделий, шт.; а — техноло- гические потери или брак, %. Число рабочих мест рассчитывается по формуле
F эф где t — время, за которое нужно выполнить программу; F эф — эф- фективный фонд времени. Начальный ритм r (d)нач определяется по формуле
j =1, n r (d) = m ax t j. j =1, n Фаза 1. Построение элементной матрицы
строка нулевая ?
åD t i ³ åw m + i j ´ t j i =1 j =1
(m + 1)-я строка нулевая ?
Конец
Рис. 11.3 é n w ù êå jt j ú r (d) = ê j = 1 ú + d, (3) нач êë m úû где m — число рабочих мест; t j — время выполнения i й элемен- тарной операции, с, мин; w j — число элементарных операций с временем t i, шт.; d — некоторая целочисленная функция:
ï åw j ´ t j
ï ï если j = 1 Ï Z ; m n åw j ´ t j
(4) ï ï0, î
если j =1
Î Z.
Конечный ритм r (d)кон находится решением следующей систе- мы:
ï j =1 í m
(5) ïå x = w, j = 1, n, ï î i =1 ij j где х ij — число элементов j на рабочем месте с номером i. Система (5) решается с помощью эвристического алгоритма (см. рис. 11.3). В фазе 1 будем пытаться удовлетворить следующим неравенс- твам:
n
j =1
(6)
причем так, чтобы x ij были неотрицательными и целыми для всех возможных i, j и чтобы выполнялись условия m å xij = w j, i =1
j = 1, n.
(7) Переход к фазе 2 алгоритма возможен при выполнении следу- ющего условия:
m n åD t i ³ å x m +1, j ´ t j . (8) i =1 j =1 Процесс обмена элементами в таблице можно записать в следу- ющем виде: t = p ¢ ´ t j - q ´ t i, (9) p £ x ij, (10) q £ x kl. (11) Функцию t необходимо вычислить для различных q, l, p ', j, k (q и p ' принимают все целочисленные значения от 1 до x kl и x ij в поряд- ке возрастания; l изменяется от n до 1 в порядке убывания; j — от 1 до n в порядке возрастания; k — от m до 1 в порядке убывания; i — от 1 до m в порядке возрастания). После вычисления каждого t необходимо проверить условия: 0 < t £ D t k. (12) При выполнении условия (12) провести расчеты по формулам:
x ij = x i ¢ j - p ¢; x il = x i ¢ l + q; Проверить условия: x k l = x k ¢ l - q; x k j = x k ¢ j + p ¢; D t i = D t i ¢ + t; D t k = D t k ¢ - t.
(13) D t l ³ t j,
x m +1, j > 0 (j =1, n).
(14) При выполнении условий (14) вычисляются новые значения:
x ij = x i ¢ j +1; D t i = D t i ¢ - t j. x m +1, i = x m ¢ +1, j -1;
(15)
2 1 В результате, если (m + 1)я строка оказывается нулевой, то за- дача решена. Если нет, то вычисляется новое значение t при пре- жних значениях i, k, j и новых значениях p' = 1, l = n, q = 1.
Пример решения задачи синхронизации поточно-конвейерной линии Произвести распределение элементарных операций по рабочим местам ПКЛ при следующих исходных данных: 1) число рабочих мест ПКЛ m = 6; 2) число элементарных операций с разным временем выполне- ния n = 6; 3) число элементарных операций для распределения с временем t j, имеющих ресурс w j: t 1 = 5 с; t 2 = 7 с; t 3 = 10 с; t 4 = 15 с; t 5 = 18 с; t 6 = 45 с; w1 = 10; w2 = 33; w3 = 25; w4 = 8; w5 = 22; w6 = 8. Определите: 1) начальный ритм работы ПКЛ; 2) конечный (оптимальный) ритм работы ПКЛ;
3) потери рабочего времени на каждом рабочем месте ПКЛ; 4) суммарные абсолютные потери рабочего времени на ПКЛ; 5) распределение элементарных операций по рабочим местам ПКЛ в фазах 1 и 2 алгоритма (привести построенные элементные матрицы); 6) относительные суммарные потери рабочего времени на ПКЛ; 7) контрольные суммы элементов по столбцам в фазе 2, сравнив с исходными данными. Решение 1. Начальное значение ритма: é n w ù êå j ´ t j ú r (d) = ê j = 1 ú + d = нач êë m úû = 5 ´10 +7 ´33 +10 ´25 +15 ´8 +18 ´22 +45 ´8 = 6
6 2. Проверка замечания 1: n r (d) ´ m ³ åw j ´ t j; 235 ´ 6 ³ 1407; 1410 > 1407. j =1
3. Проверка замечания 2: r (d) ³ m ax t j; 235 > 45 — замечание выполняется. j =1, n 4. Формирование строк элементной матрицы.
Фаза 1. 1. Формирование первой строки. x 11 t 1 £ r; 1 ´ 5 £ 235; 2 ´ 5 £ 235; …; 5 ´ 10 £ 235; 5 ´ 11 £ 235; x 11 £ w1; 1<10; 2<10; …; 10 = 10; 11>10 — условие (x 11 £ w1) не выполняется. Возвращение к предыдущему шагу. Поскольку все элементы со временем t 1 выбраны, берем элемен- ты со временем t 2: x 12 t 2 £ 235 – 5 ´ 10; 1 ´ 7 £ 185; 2 ´ 7 £ 185; …; 26 ´ 7 £ 185; 27 ´ ´ 7 ³ 185; x 12 £ w2; 1 < 33; 2 < 33; …; 26 < 33; 27 < 33 — условие (x 12 t 2 £ £ 235 — 5 ´ 10) не выполняется. Возвращение к предыдущему шагу. 2. Определение оставшегося количества элементов с време- нем t 2: w22 = w2 – x 12 = 33 – 26 = 7. 3. Определение возможности помещения элементов с време- нем t 3:
2 x 13 t 3 £ 235 – (50 + 182); 1 ´ 10 > 235 – 232 — условие (x 13 t 3 £ £ 235 – (50 + 182)) не выполняется. x 13 = 25; 1 < 25. Значит, помещать эти элементы в первую строку нельзя. По- скольку времена выполнения оставшихся элементов возрастают, то их помещать также нельзя. В противном случае требуется про- верка возможности помещения всех остальных элементов. Таким образом, первая строка элементной матрицы имеет вид:
4. Формирование второй строки. Так как элементы с временем t 1 все помещены в первую строку, они не рассматриваются для помещения во вторую и все оставши- еся строки. Размещаются все оставшиеся элементы с временем t 2:. x 22 t 2 £ 235; 1 ´ 7 £ 235; 2 ´ 7 £ 235; …; 7 ´ 7 £ 235; 8 ´ 7 £ 235; x 22 £ 7; 1 < 7; 2 < 7; …; 7 = 7; 8 > 7 — условие (x 22 £ 7) не выпол- няется. Возвращение к предыдущему шагу. Все 7 элементов с вре- менем t 2 размещены в строке T 2. Размещение элементов с временем t 3 во вторую строку:
x 23 t 3 £ 235 – 49; 1 ´ 10 £ 186; 2 ´ 10 £ 186; …; 18 ´ 10 < 186; 19 ´ 10 > 186; x 23 £ 25; 1 < 25; 2 < 25; …; 18 < 25; 19 < 25 — условие (x 23 t 3 £ £ 235 – 49) не выполняется. Возвращение к предыдущему шагу. Помещение элементов с временем t 4 невозможно, так как r (d) — – S x 2 j ´ t j < t 4; 235 — (49 + 180) = 6 < 15. Вторая строка элементной матрицы имеет вид:
5. Формирование третьей строки. Определение оставшегося количества элементов с време- нем t 3: w33 = w3 — x 23 = 25 — 18 = 7. Размещение оставшихся элементов с временем t 3 в третью строку: x 33 t 3 £ 235; 1 ´ 10 £ 235; 2 ´ 10 £ 235; …; 7 ´ 10 £ 235; 8 ´ 10 £ 235; x 33 £ 7; 1< 7; 2 < 7; …; 7 = 7; 8 > 7 — условие (x 33 £ 7) не выпол- няется. Возвращение к предыдущему шагу. Размещение элементов с временем t 4 в третью строку: x 34 t 4 £ 235 — 70; 1 ´ 15 £ 165; 2 ´ 15 £ 165; …; 8 ´ 15 £ 165; 9 ´ 15 £ 165; x 34 £ 8; 1< 8; 2< 8; …; 8 = 8; 9 > 8 — условие (x 34 £ 8) не выполня- ется. Возвращение к предыдущему шагу. Размещение элементов с временем t 5 в третью строку: x 35 t 5 £ 235 – (70+120); 1 ´ 18 £ 45; 2 ´ 18 £ 45; …; 3 ´ 18 > 45; x 35 £ 22; 1 < 22; 2 < 22; …; 3 < 22 — условие (x 35 t 5 £ 235 – (70+120)) не выполняется. Возвращение к предыдущему шагу. Третья строка элементной матрицы имеет вид:
6. Формирование четвертой строки. Определение оставшегося количества элементов t 5: w45 = w5 — x 35 = 22 — 2 = 20. Размещение элементов с временем t 5 в четвертую строку: x 45 t 5 £ 235; 1´18 £ 235; 2´18 £ 235; …; 13´18 < 235; 14´18 > 235; x 45 £ 20; 1 < 20; 2 < 20; …; 13 < 20; 14 < 20 — условие (x 45 t 5 £ 235) не выполняется. Возвращение к предыдущему шагу. Помещение элементов с временем t 6 невозможно, так как r (d) – S x 4 j ´ t j < t 6, т.е. 235 — 234 = 1 < 18. Четвертая строка элементной матрицы имеет вид:
7. Формирование пятой строки. Определение оставшегося количества элементов с време- нем t 5: w55 = w5 — (x 35 — x 45) = 22 — (2 + 13) = 7.
2 5 Размещение элементов со временем t 5 в пятую строку: x 55 t 5 £ 235; 1 ´ 18£ 235; 2 ´ 18 £ 235; …; 7 ´ 18 £ 235; 8 ´ 18 £ 235; x 55 £ 7; 1< 7; 2< 7; …; 7 = 7; 8 > 7 — условие (x 55 £ 7) не выполня- ется. Возвращение к предыдущему шагу. Размещение элементов с временем t 6 в пятую строку: x 56 t 6 £ 235 – 126; 1 ´ 45 £ 109; 2 ´ 45 £ 109; 3 ´ 45 > 109; x 56 £ 8; 1 < 8; 2 < 8; 3 < 8 — условие (x 56 t 6 £ 235 – 126) не выпол- няется. Возвращение к предыдущему шагу. Пятая строка элементной матрицы имеет вид:
8. Формирование шестой строки. Определение оставшегося количества элементов с време- нем t 6: w66 = w6 — x 56 = 8 — 2 = 6. Размещение элементов с временем t 6 в шестую строку: x 66 t 6 £ 235; 1 ´ 45 £ 235; 2 ´ 45 £ 235; …; 5 ´ 45 £ 235; 6 ´ 45 > 235; x 66 £ 6; 1 < 6; 2 < 6; …; 5 < 6; 6 = 6 — условие (x 66 t 6 £ 235) не вы- полняется. Возвращение к предыдущему шагу. Шестая строка элементной матрицы имеет вид:
9. Формирование (m + 1)й строки. Определение оставшегося количества элементов с временем t 6 для формирования (m + 1)й строки: w m +1,6 = w6 — (x 56 + x 66) = 8 — (2 +5) = 1. (m + 1)я строка элементной матрицы имеет вид:
10. Элементная матрица после фазы 1 имеет вид:
(m + 2)я строка является контрольной. Она показывает, все ли элементы распределены, сравнением контрольной суммы по стол- бцам и исходных данных можно в этом убедиться. Поскольку в (m + 1)й строке есть один элемент, это говорит о том, что на первой фазе задача не решена. Требуется применение фазы 2. Для этого необходимо проверить условие: m n åD t i ³ å x m +1, j ´ t j; 48 > 45 i =1
– условие выполняется. Фаза 2. j =1 1. Выбираем две строки и два столбца, где i = 1, k = 6, j = 1, l = 6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.54 (0.248 с.) |

 T = { t j t j Î N, j = 1, n };
T = { t j t j Î N, j = 1, n };
 W = {w j w j Î N, j = 1, n },
W = {w j w j Î N, j = 1, n },

 ïå xij ´ t j £ r, i = 1, m;
ïå xij ´ t j £ r, i = 1, m;

 N = N в ´100 , (1)
N = N в ´100 , (1) m = N з ´ t, (2)
m = N з ´ t, (2)
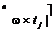
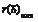
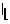
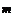
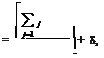 r (d) = m ax t j.
r (d) = m ax t j. m
m

 = 1407 = 234,5 = 234 + 0,5 = 235 c.
= 1407 = 234,5 = 234 + 0,5 = 235 c.


