
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы и обозначения ⇐ ПредыдущаяСтр 3 из 3
Расчет любой разветвленной цепи можно произвести, пользуясь двумя правилами Кирхгофа. Первое правило Кирхгофа (для узлов цепи):
где Второе правило (для замкнутых контуров цепи):
где При решении задач на расчет разветвленной цепи необходимо: 1) произвольно выбрать и указать стрелкой направление тока на каждом неразветвленном участке цепи; 2) для цепи, содержащей N узлов, записать первое правило Кирхгофа для 3) определить число 4) определить число независимых замкнутых контуров в цепи: 5) найти любые М независимых контуров (например, если 6) произвольно выбрать направление обхода каждого взятого контура (по ходу часовой стрелки или против него); 7) для каждого взятого контура записать второе правило Кирхгофа; 8) решить полученную систему уравнений (она имеет решение, если число независимых уравнений равно числу неизвестных), например, методом Гаусса или методом Крамера. Если значение силы тока на каком-то участке окажется отрицательным, то в действительности ток течет на этом участке в противоположном направлении.
З а д а ч а 18. В схеме на рис. 16
Для расчета с помощью правил Кирхгофа выберем направление тока на каждом неразветвленном участке цепи (они указаны стрелкой на схеме рис. 16). Запишем первое правило Кирхгофа для любого из двух узлов, например, для узла А:
Сила тока Для данной цепи на основе первого и второго правил Кирхгофа может быть составлено три независимых уравнения, так как она содержит три неразветвленных участка. Следовательно, с учетом уравнения (46) достаточно рассмотреть два независимых контура, например, контуры AGBDА и AFBGА. Выбранные произвольно направления обхода этих контуров («по часовой стрелке») указаны на схеме. Уравнения, составленные по второму правилу Кирхгофа для контуров AGBDА и AFBGА соответственно, имеют вид:
ЭДС Подставляя известные численные значения сопротивлений участков цепи и ЭДС источников тока в уравнения (46) – (48), получим систему трех линейных уравнений с тремя неизвестными
Решение такой системы дается формулами Крамера:
где Определители вычисляются по значениям коэффициентов системы (49):
Подставив в формулу (50) значения соответствующих определителей, получим: Заметим, что при решении системы (49) методом подстановок удобно выразить силы тока
и, подставив выражения в первое уравнение: Ответ:
Библиографический список 1. Т р о ф и м о в а Т. И. Краткий курс физики / Т. И. Т р о ф и м о в а. М., 2012. 352 с. 2. Д е т л а ф А. А. Курс физики / А. А. Д е т л а ф, Б. М. Я в о р с к и й. М., 2014. 720 с. 3. С а в е л ь е в И. В. Курс общей физики: В 5 т. Т. 2. Электричество и магнетизм / И. В. С а в е л ь е в. СПб, 2011. 348 с. 4. Практикум по физике. Часть 2. Электричество и магнетизм. Колебания: Методические указания к решению задач по физике / Т. А. А р о н о в а, С. В. Вознюк и др. / Омский гос. ун-т путей сообщения. Омск, 2014. 40 с. 5. К р о х и н С. Н. Контрольная работа № 2 по физике для студентов заочного факультета: Методические указания к решению задач и выполнению контрольных работ для студентов заочного факультета / С. Н. К р о х и н, Ю. М. С о с н о в с к и й / Омский гос. ун-т путей сообщения. Омск, 2012. 36 c.
Учебное издание
КУРМАНОВ Рамиль Султангареевич, ТОДЕР Георгий Борисович
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Учебно-методическое пособие
*** Подписано в печать 13.10.2016. Формат 60 ´ 84 1/16. Офсетная печать. Бумага офсетная. Усл. печ. л. 1,7. Уч.-изд. л. 1,9. Тираж 800 экз. Заказ .
** Редакционно-издательский отдел ОмГУПСа Типография ОмГУПСа
* 644046, г. Омск, пр. Маркса, 35
|
||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 113; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.108 (0.016 с.) |
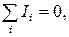 (44)
(44) – алгебраическая сумма сил токов, сходящихся в узле: сила тока, текущего к узлу, входит в уравнение (44) со знаком «+», а тока, текущего от уз-ла, – со знаком «–».
– алгебраическая сумма сил токов, сходящихся в узле: сила тока, текущего к узлу, входит в уравнение (44) со знаком «+», а тока, текущего от уз-ла, – со знаком «–».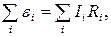 (45)
(45)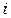 – номер неразветвленного участка контура, который характеризуется током силой
– номер неразветвленного участка контура, который характеризуется током силой  , полным сопротивлением
, полным сопротивлением 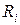 и падением напряжения
и падением напряжения 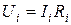 ;
;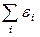 – алгебраическая сумма ЭДС контура: если направления обхода контура и действия сторонних сил внутри источника совпадают, то ЭДС входит в уравнение (45) со знаком «+», если противоположны, – со знаком «–»;
– алгебраическая сумма ЭДС контура: если направления обхода контура и действия сторонних сил внутри источника совпадают, то ЭДС входит в уравнение (45) со знаком «+», если противоположны, – со знаком «–»;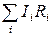 – алгебраическая сумма падений напряжения в контуре: если направления обхода контура и тока на участке совпадают, то сила тока входит в уравнение (45) со знаком «+», если противоположны, – со знаком «–».
– алгебраическая сумма падений напряжения в контуре: если направления обхода контура и тока на участке совпадают, то сила тока входит в уравнение (45) со знаком «+», если противоположны, – со знаком «–».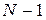 узлов (например, если
узлов (например, если 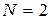 , то для одного любого узла);
, то для одного любого узла);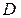 независимых уравнений, которые могут быть составлены на основе первого и второго правил Кирхгофа, оно равно числу неразветвленных участков цепи (числу различных токов);
независимых уравнений, которые могут быть составлены на основе первого и второго правил Кирхгофа, оно равно числу неразветвленных участков цепи (числу различных токов);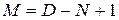 (например, если
(например, если 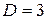 , то
, то 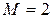 );
); 4.2.2. Примеры решения задач
4.2.2. Примеры решения задач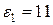 В,
В, 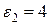 В,
В, 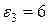 В,
В, 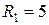 Ом,
Ом, 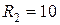 Ом,
Ом, 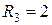 Ом, внутренние сопротивления источников тока пренебрежимо малы. Определить силы токов, текущих через сопротивления.
Ом, внутренние сопротивления источников тока пренебрежимо малы. Определить силы токов, текущих через сопротивления.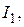
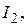
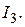
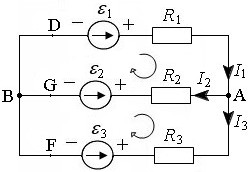 Рис. 16
Рис. 16
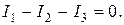 (46)
(46)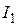 входит в уравнение со знаком «+», так как этот ток втекает в узел, силы тока
входит в уравнение со знаком «+», так как этот ток втекает в узел, силы тока 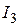 – со знаком «–», так как эти токи вытекают из узла.
– со знаком «–», так как эти токи вытекают из узла.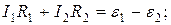 (47)
(47) (48)
(48)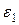 входит в уравнение (47), а
входит в уравнение (47), а 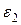 – в уравнение (48) со знаком «+», так как направления обхода контуров и действия сторонних сил внутри источника на соответствующих участках совпадают (см. рис. 16). ЭДС
– в уравнение (48) со знаком «+», так как направления обхода контуров и действия сторонних сил внутри источника на соответствующих участках совпадают (см. рис. 16). ЭДС 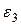 – в уравнение (48) со знаком «–», так как направления обхода контура и действия сторонних сил противоположны. Силы тока
– в уравнение (48) со знаком «–», так как направления обхода контура и действия сторонних сил противоположны. Силы тока 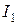 и
и 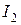 входят в уравнение (47), а сила тока
входят в уравнение (47), а сила тока 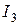 – в уравнение (48) со знаком «+», так как направления обхода контура и тока на соответствующих участках совпадают. Сила тока
– в уравнение (48) со знаком «+», так как направления обхода контура и тока на соответствующих участках совпадают. Сила тока 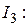
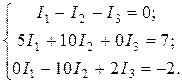 (49)
(49)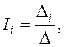
 (50)
(50)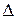 – определитель системы (49);
– определитель системы (49);  – определитель при неизвестном
– определитель при неизвестном 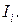
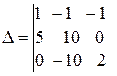
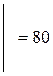 ;
; 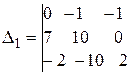
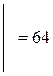 ;
;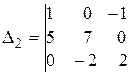
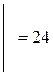 ;
; 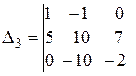
 .
.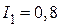 А,
А, 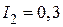 А,
А, 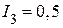 А.
А. ; (51)
; (51)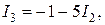 (52)
(52)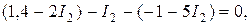 найти силу тока
найти силу тока 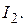 После подстановки значения
После подстановки значения 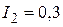 А в соотношения (51), (52) вычисляются значения сил тока
А в соотношения (51), (52) вычисляются значения сил тока 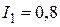 А;
А; 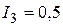 А.
А. Редактор Н. А. Майорова
Редактор Н. А. Майорова


