Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепь переменного тока с активно-индуктивной нагрузкой
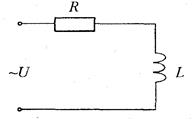
Теперь рассмотрим электрическую цепь (рис. 2.13), в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток: I = I 0 sin ω t 2. 4
Через катушку и через резистор протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем искать вектор напряжения, приложенного к этой цепи. Рис. 2. 13
Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе. Из векторной диаграммы видим, что напряжение на индуктивности опережает ток на 90о:
Закон Ома для цепи с идеальной индуктивностью (т.е. не обладающей активным сопротивлением) выглядит так: 2.6, величина xL называется индуктивным сопротивлением. Построив векторы I, UR и UL и воспользовавшись формулой (2.5), найдем вектор U. Векторная диаграмма для этой цепи показана на рис. 2.14.
Рис. 2. 14 Величина
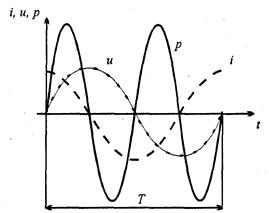
называется полным сопротивлением цепи. Сдвиг по фазе между током и напряжением также определяется из векторной диаграммы. В данной цепи угол сдвига фаз между током и напряжением зависит от значений R и L и изменяется в пределах от 0 до 90о. Рассмотрим теперь, как изменяется со временем мощность в цепи с активно-индуктивной нагрузкой. Мы видим, что мгновенное значение мощности имеет две составляющие: первое слагаемое – активная, и второе – реактивная (индуктивная). Поэтому средняя за период мощность не равна нулю. Соответствующая этой мощности электрическая энергия превращается в активном сопротивлении R в теплоту.
Условным обозначением емкости является символ C (рис. 2.15) Рис. 2. 15
Рассмотрим электрическую цепь, в которой переменное напряжение приложено к емкости С (рис. 2.16). Векторная диаграмма показана на рис. 2.17. Мгновенное значение тока в цепи с емкостью равно скорости изменения заряда на обкладках конденсатора (2.8).
Рис. 2. 16 Рис. 2. 17
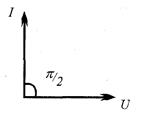
В этой цепи ток опережает напряжение на 90о.
Закон Ома для цепи переменного тока с емкостью (2.9), а величина хс называется емкостным сопротивлением. Векторная диаграмма для этой цепи показана на рис. 2.18.
Рис. 2. 18
В этой цепи мгновенная мощность изменяется с удвоенной частотой (рис. 2.18). При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные – его разряду и возврату запасенной энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергией между конденсатором и источником.
|
|||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 84; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.179 (0.005 с.) |
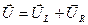 2. 5
2. 5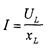 2. 6
2. 6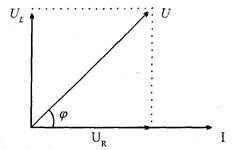
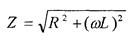 2. 7
2. 7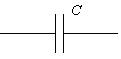 2.8. Цепь переменного тока с емкостью
2.8. Цепь переменного тока с емкостью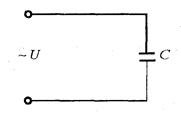
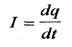 2. 8
2. 8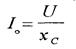 2. 9
2. 9