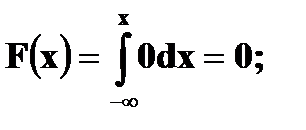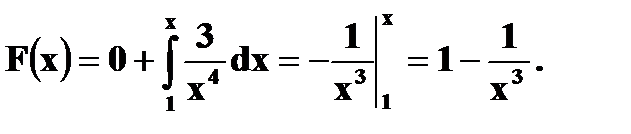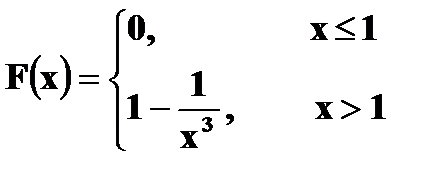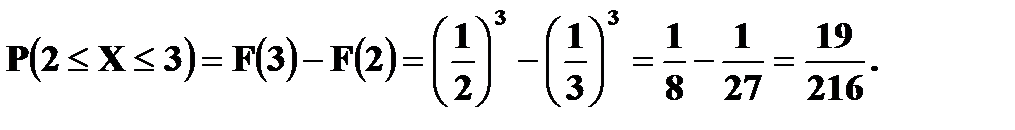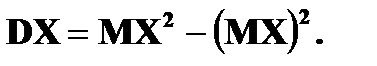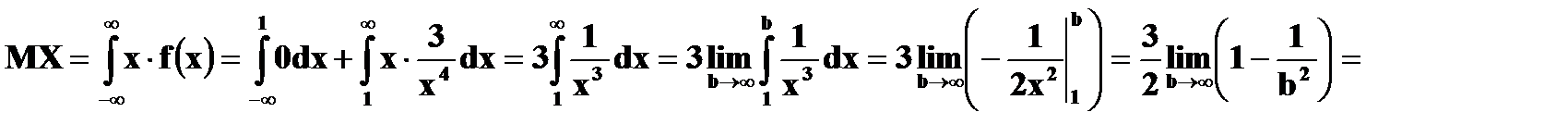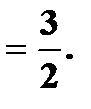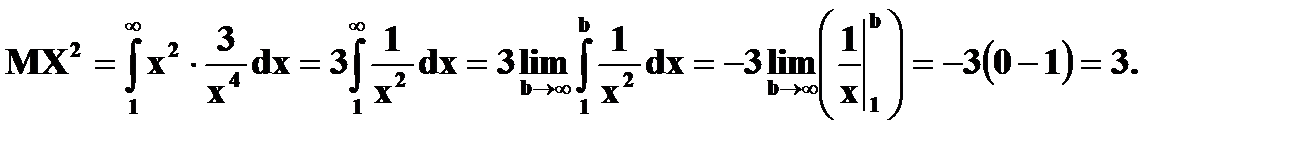Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция распределения случайной величины.
Определение. Функцией распределения случайной величины Геометрически: функция распределения
Пример. Дан ряд распределения случайной величины
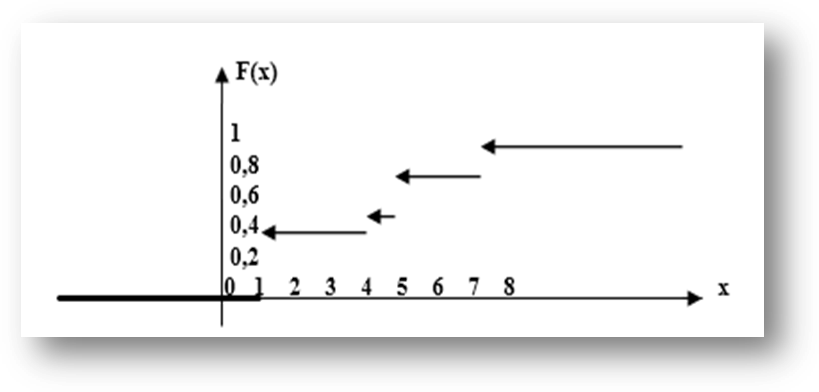
Найти и изобразить графически ее функцию распределения. Решение. 1. x ≤ 1 F (x) = 0 ( в том числе и для x = 1, так как F(1) = P(X<1)) 2. 1 < x ≤ 4 F (x) = P (X = 1) = 0, 4 (в том числе и для x = 4) 3. 4 < x ≤ 5 F (x) = P (X = 1) + P (X = 4) = 0, 5 (в том числе и для x = 5) 4. 5 < x ≤ 7 F(x) = P(X = 1) + P(X = 4) + P(X = 5) = 0, 5 + 0, 3 = 0,8 5. x > 7 F(x) = P(X = 1) + P(X = 4) + P(X=5) + P(X = 7) = 0,8 + 0,2 =1
Итак,
Заметим, что при переходе слева к точкам разрыва функция F(x) сохраняет свои значения, то есть F(x) – непрерывна слева. Из графика видно, что F(x) – разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции распределения равна 1.
Свойства функции распределения: 1. 0 ≤ F(x) ≤ 1 2. Функция распределения F(x) есть неубывающая функция на всей числовой прямой. 3. 4. Вероятность попадания случайной величины
Пример. Функция распределения
Найти Решение. P (1 ≤ X < 3) = Непрерывные случайные величины. Плотность вероятности Определение. Плотностью вероятности (плотностью распределения или просто плотностью) f(x) непрерывной случайной величины
График плотности вероятности называют кривой распределения.
Свойства плотности: 1. 2. Вероятность попадания случайной величины
3.Функция распределения
4. Геометрическая интерпретация свойств 2 и 3:
Первое свойство означает, что кривая распределения лежит не ниже оси x, а свойство 4 – полная площадь фигуры, ограниченной кривой распределения и осью 0x равна 1.
Для непрерывной случайной величины числовые характеристики имеют вид:
(если интегралы сходятся). Пример. Функция f(x) задана в виде:
Найдите: a) значение постоянной А, при которой функция будет плотностью вероятности некоторой случайной величины X; б) выражение функции распределения F(x); в) вычислите вероятность того, что случайная величина X примет значения на отрезке г) найдите математическое ожидание и дисперсию случайной величины X. Решение. а) Чтобы f(x) была плотностью вероятности некоторой случайной величины X, она должна быть неотрицательной и Следовательно,
Имеем б) Если Если X > 1, то Получаем, что
в) г)
Некоторые законы распределения
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 63; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.240.243 (0.007 с.) |
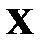 назовем функцию
назовем функцию 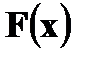 , выражающую для любого
, выражающую для любого 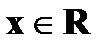 вероятность того, что случайная величина
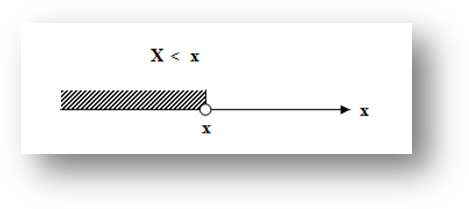
вероятность того, что случайная величина 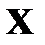 примет значения, меньше
примет значения, меньше 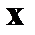 :
:  (X< x).
(X< x).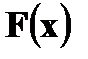 – это вероятность попасть случайной величине
– это вероятность попасть случайной величине 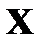 левее заданной точки
левее заданной точки 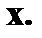
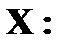
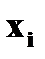
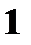

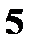

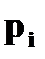
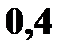
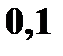
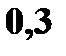
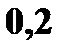
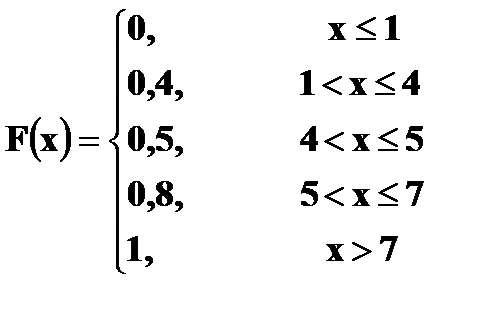
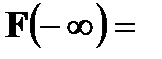 lim
lim 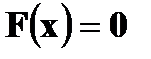 ,
, 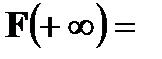 lim
lim 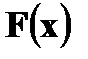 =1
=1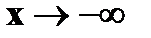
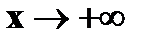
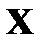 в интервал
в интервал 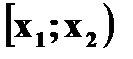 равна приращению ее функции распределения, то есть
равна приращению ее функции распределения, то есть 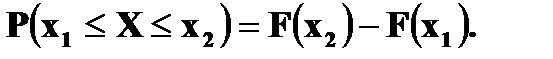
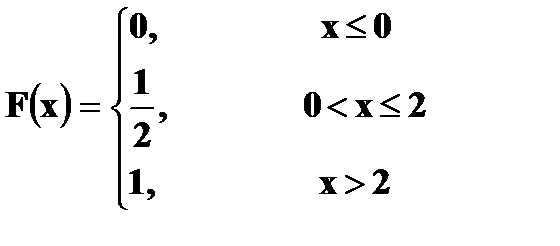
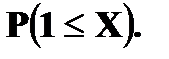
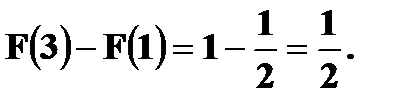

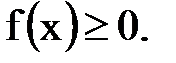
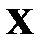 в интервал
в интервал 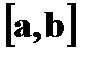 равна
равна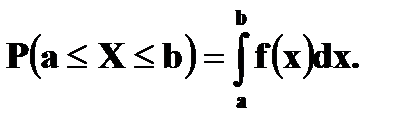
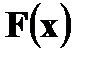 выражается через плотность
выражается через плотность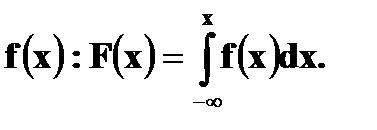
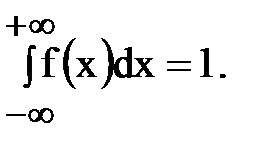

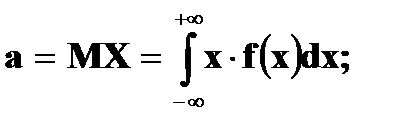
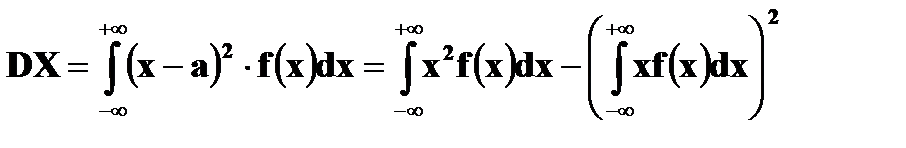

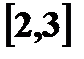 ;
;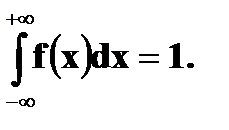
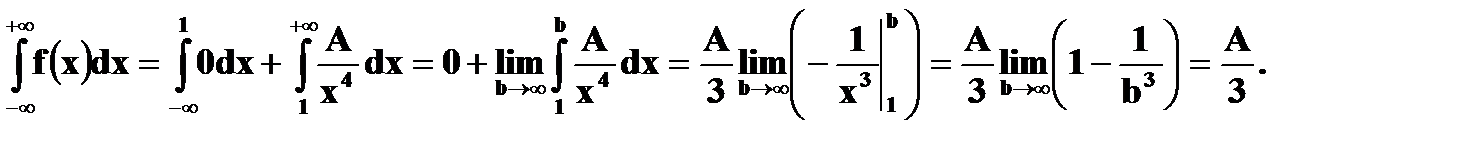
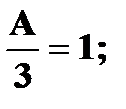 тогда
тогда 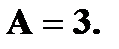
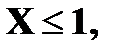 то
то