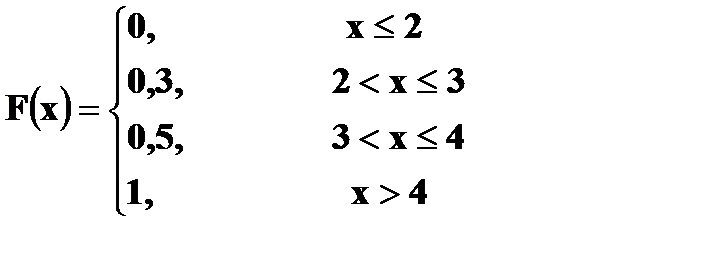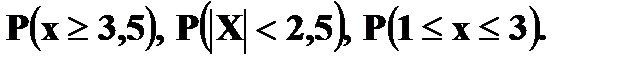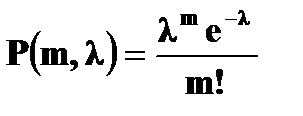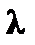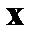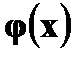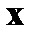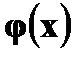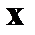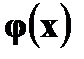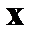Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд распределения случайной величиныСтр 1 из 4Следующая ⇒
Случайные величины 1. Понятие случайной величины. Закон распределения дискретной случайной величины. Под случайной величиной понимают переменную, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее не известно). Примеры случайных величин: 1) количество бракованных изделий в данной партии; 2) число произведенных выстрелов до первого попадания; 3) время ожидания транспорта при поездке на работу; 4) курс доллара в определенный день; 5) число новорожденных в городе Донецке в течение часа; 6) число дней в году. Разберем последний пример более подробно. Результат испытания 365 или 366 зависит от того год обычный или високосный. Если назвать любой исход эксперимента элементарным событием (обозначается Договоримся случайные величины обозначать прописными буквами латинского алфавита X, Y, Z, …, а их значения соответствующими строчными x, y, z, … В нашем примере случайная величина X – число дней в году – является функцией элементарных исходов;
Случайная величина, принимающая конечное или счетное число значений на числовой прямой, называется дискретной. В разобранном случае речь шла о дискретной случайной величине, ибо она принимала два значения: 365 и 366. Если же случайная величина принимает непрерывное множество значений (например, значения на всей числовой прямой, на полупрямой, на отрезке), то ее называют непрерывной. Простейшая форма задания закона распределения дискретной случайной величины X является таблица, в которой перечислены в порядке возрастания различные возможные значения случайной величины и соответствующие им вероятности.
Такая таблица называется рядом распределения. Ясно, что Можно закон распределения определить формулой Если число значений случайной величины счетно, то
Пример 1. В лотерее разыгрывается автомобиль стоимостью в 5000 у. е., 4 телевизора стоимостью 250 у. е., 5 видеомагнитофонов стоимостью 200 у. е. Всего продается 1000 билетов по 7 у. е. Составить закон распределения чистого выигрыша, полученного участником лотереи, купившим 1 билет. Решение. Возможные значения случайной величины X – чистого выигрыша на 1 билет:
То есть ряд распределения
Пример 2. Вероятность того, что студент сдаст семестровые экзамены по дисциплинам А и Б, равна соответственно 0, 7 и 0, 9. Составить закон распределения числа семестровых экзаменов, которые сдаст студент. Решение. Возможные значения случайной величины X – числа сданных экзаменов могут быть 0, 1 и 2. Пусть
Дисперсия Дисперсией DX случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания, то есть Если Средним квадратическим отклонением (стандартным отклонением или стандартом) Свойства дисперсии: 1. 2. 3. 4. Если
Пример. Найти Решение. По свойствам 4, 2
Решение. 1. x ≤ 1 F (x) = 0 ( в том числе и для x = 1, так как F(1) = P(X<1)) 2. 1 < x ≤ 4 F (x) = P (X = 1) = 0, 4 (в том числе и для x = 4) 3. 4 < x ≤ 5 F (x) = P (X = 1) + P (X = 4) = 0, 5 (в том числе и для x = 5) 4. 5 < x ≤ 7 F(x) = P(X = 1) + P(X = 4) + P(X = 5) = 0, 5 + 0, 3 = 0,8 5. x > 7 F(x) = P(X = 1) + P(X = 4) + P(X=5) + P(X = 7) = 0,8 + 0,2 =1
Итак,
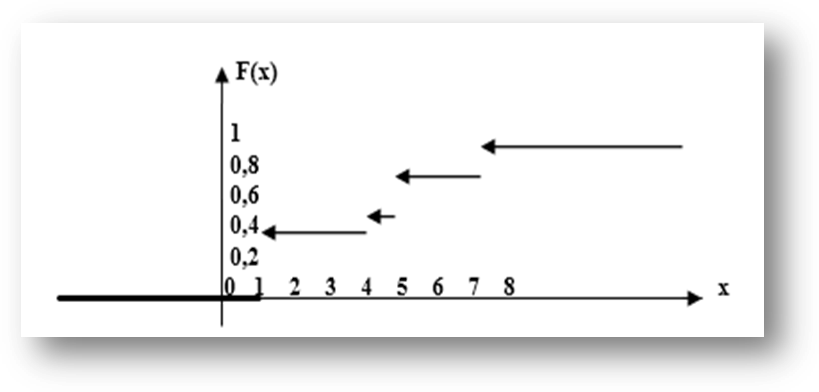
Заметим, что при переходе слева к точкам разрыва функция F(x) сохраняет свои значения, то есть F(x) – непрерывна слева.
Из графика видно, что F(x) – разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции распределения равна 1.
Свойства функции распределения: 1. 0 ≤ F(x) ≤ 1 2. Функция распределения F(x) есть неубывающая функция на всей числовой прямой. 3. 4. Вероятность попадания случайной величины
Пример. Функция распределения
Найти Решение. P (1 ≤ X < 3) = Решение. а) Чтобы f(x) была плотностью вероятности некоторой случайной величины X, она должна быть неотрицательной и Следовательно,
Имеем б) Если Если X > 1, то Получаем, что
в) г)
Равномерное распределение Непрерывная случайная величина X имеет равномерный закон распределения на отрезке
Тогда
Решение задач 1. Подбрасываются две симметричные монеты, подсчитывается число гербов на обеих верхних сторонах монет. Записать закон распределения случайной величины X – число выпадений гербов на обеих монетах. Решение. В данном опыте пространство элементарных исходов Ω = {(ГГ), (РР), (ГР), (РГ)}. Герб может выпасть 1 раз, 2 раза и ни разу.
Закон распределения случайной величины X:
2. Радист вызывает корреспондента, причем каждый последующий вызов производится лишь в том случае, если предыдущий вызов не принят. Вероятность того, что корреспондент примет вызов, равна Найдите математическое ожидание и дисперсию этой случайной величины. Решение.а) Случайная величина X – число вызовов корреспондента – может принимать значения 1, 2, 3, 4, 5. Пусть Аналогично,
Пятый вызов при любом исходе – последний.
Ряд распределения случайной величины X имеет вид:
Математическое ожидание
Дисперсия
б) Так как число вызовов не ограничено, то ряд распределения случайной величины X имеет вид:
Проверка: ( Сумма ряда в скобках – это сумма бесконечно убывающей геометрической прогрессии,
Для вычисления суммы ряда воспользуемся формулой
В нашем случае
Для вычисления суммы, записанной в скобках, сначала рассмотрим сумму ряда
При
3. Ряд распределения дискретной случайной величины состоит из двух неизвестных значений. Вероятность того, что случайная величина примет одно из значений равна 0,8. Найти функцию распределения случайной величины, если ее математическое ожидание равно 3,2 и ее дисперсия равна 0,16. Решение. Пусть значения случайной величины X равны
Известно, что Значит, что Решая систему, находим два решения: Поэтому
4. Дана функция распределения случайной величины X:
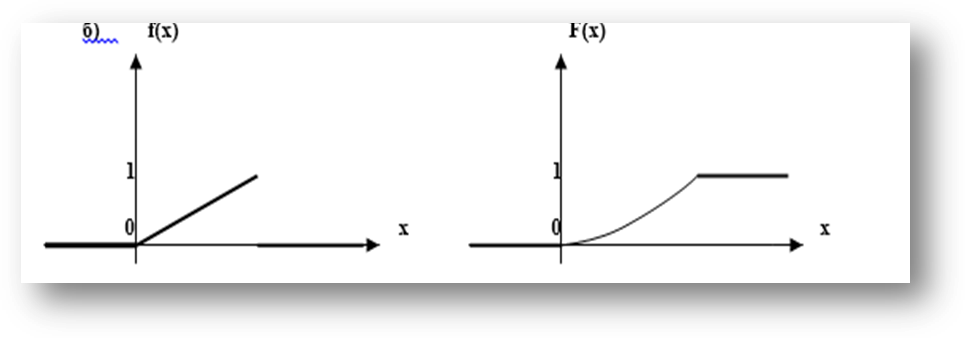
а) Найти плотность вероятности б) Построить графики в) Найти вероятности г) Вычислить Решение. а) Плотность вероятности
б)
в) г)
Упражнения 1. Может ли закон распределения какой – либо случайной величины быть задан таблицей:
а)
б)
2. Вероятность того, что в библиотеке есть необходимая студенту книга равняется 0,3. Составьте закон распределения случайной величины X – числа библиотек, которые посетит студент (студент прекращает последовательное посещение библиотек, если в какой – либо из них обнаружит нужную книгу). 3. Проводится розыгрыш 1000 билетов лотереи, в которой 100 билетов дают выигрыш по 1 гривне, 10 билетов – по 10 гривень, 1 билет – 100 гривень. Какой выигрыш в среднем приходится на билет? Известно, что билеты продают по 1 гривне. 4. Дискретная случайная величина X принимает 3 значения 5. Дискретная случайная величина X принимает 2 значения 6. Клиенты банка, не связанные друг с другом, не возвращают кредиты в долг с вероятностью 0, 1. Составьте закон распределения числа возвращенных в срок кредитов из 5 выданных. Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. 7. В билете 3 задачи. Вероятность правильного решения первой задачи равняется 0, 9, второй – 0,8, а третьей – 0,7. Составьте закон распределения числа правильно решенных задач в билете; вычислите
8. Произведено 2 выстрела в мишень. Вероятность попадания в мишень первым стрелком равна 0, 8, а вторым – 0,7. Составьте закон распределения числа попаданий в мишень. Найдите 9. Имеются 4 ключа, из которых только 1 подходит к замку. Составьте закон распределения числа попыток открыть замок, если испробованный ключ в последующих попытках не участвует. Постройте функцию распределения 10. По многолетним статистическим данным известно, что вероятность рождения мальчика 0, 515. Составьте закон распределения случайной величины X числа мальчиков в семье из 4 детей. Найдите 11. В среднем по 10 % договоров страховая компания выплачивает страховые суммы в связи с наступлением страхового случая. Составьте закон распределения числа таких договоров среди наудачу выбранных четырех. Вычислите 12. Дана функция распределения случайной величины X
Найдите: а) закон распределения случайной величины 13. Даны законы распределения независимых случайных величин X и Y
Найдите вероятности, с которыми X и Y принимают значение 3. Составьте закон распределения случайной величины 14. На двух автоматических станках производятся одинаковые изделия. Даны законы распределения числа бракованных изделий, производимых в течение смены на каждом из них: а) для первого
б) для второго
а) Составьте закон распределения числа производимых в течение смены бракованных изделий обоими станками; б) Проверьте свойство математического ожидания суммы случайных величин. 15. Случайная величина X сосредоточена на интервале 16. Случайная величина X, сосредоточенная на интервале 17. Случайная величина X задана функцией распределения
Найдите: а) плотность вероятности б) в) г) Постройте графики функций 18. При каком a функция
будет плотностью некоторой случайной величины? Вычислить: а) 19. Случайная величина X задана функцией распределения
Определите: 1) Плотность 20. Случайная величина X задается функцией распределения
Определите 21. Случайная величина X задается функцией распределения
Определите вероятность того, что в результате двух независимых испытаний случайная величина X оба раза попадет в интервал
22. Случайная величина X задана функцией распределения
Постройте закон распределения случайной величины X. Вычислите:
ТАБЛИЦЫ Таблица 1 Закон распределения Пуассона
Продолжение таблицы 1
Таблица 2 Таблица значений функции
Продолжение таблицы 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.189.177 (0.127 с.) |
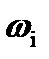 ), а все возможные события пространством элементарных событий (обозначается
), а все возможные события пространством элементарных событий (обозначается  ), то для нашего случая
), то для нашего случая 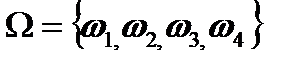 , где
, где 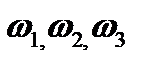 — обычные годы, а
— обычные годы, а 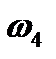 — високосный год.
— високосный год.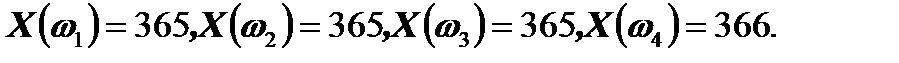
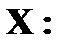 X:
X: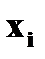
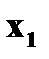
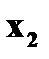

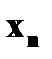
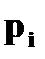
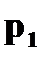
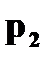

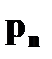
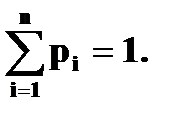
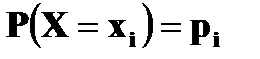
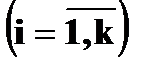 .
.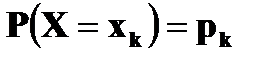
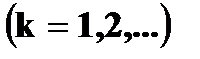
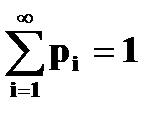 .
.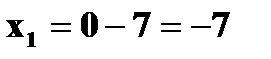 (если билет не выиграл);
(если билет не выиграл); 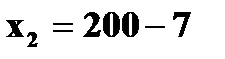 (если на билет выпал выигрыш видеомагнитофона);
(если на билет выпал выигрыш видеомагнитофона); 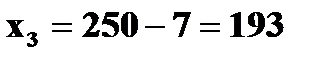 (если на билет выпал выигрыш телевизора);
(если на билет выпал выигрыш телевизора); 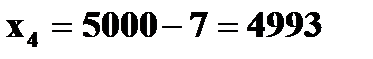 (если на билет выпал выигрыш автомобиля). Подсчитаем соответствующие этим значениям случайной величины вероятности.
(если на билет выпал выигрыш автомобиля). Подсчитаем соответствующие этим значениям случайной величины вероятности.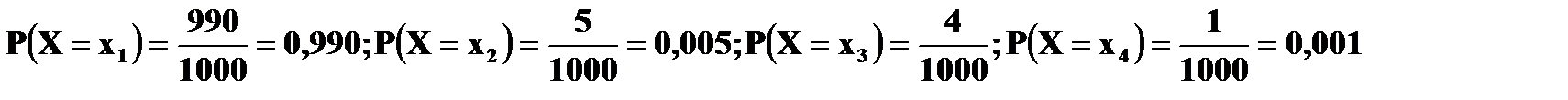
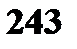
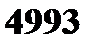
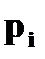
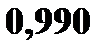
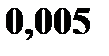
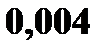
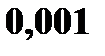
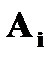 – студент сдаст i – ый экзамен.
– студент сдаст i – ый экзамен. 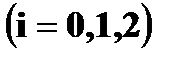
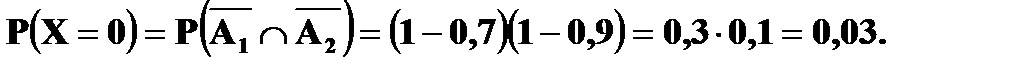
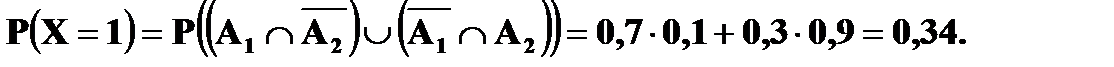
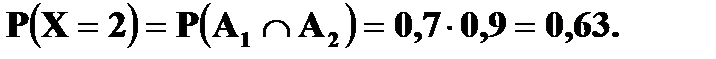
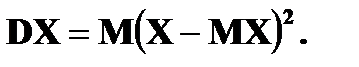
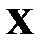 – дискретная случайная величина и
– дискретная случайная величина и 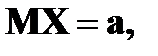 то
то 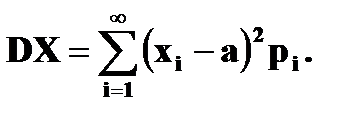
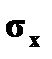 случайной величины
случайной величины 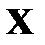 называется арифметическое значение корня квадратного из ее дисперсии.
называется арифметическое значение корня квадратного из ее дисперсии.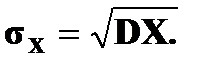
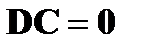 , где
, где 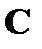 – постоянная;
– постоянная;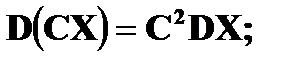
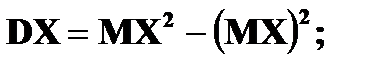
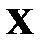 и
и 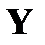 — независимые случайные величины, то
— независимые случайные величины, то 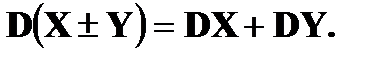
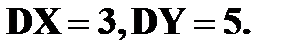
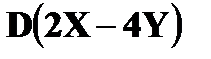 .
.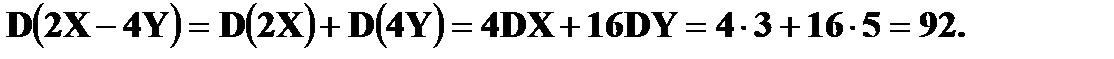
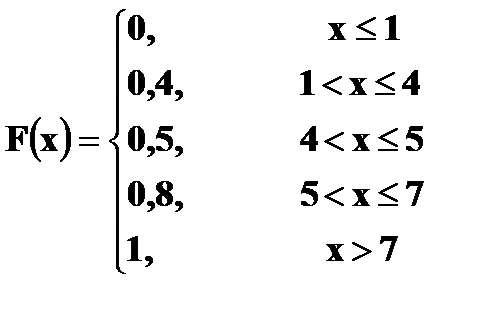
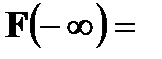 lim
lim 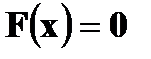 ,
, 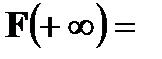 lim
lim 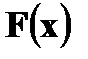 =1
=1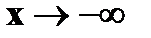
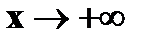
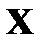 в интервал
в интервал 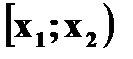 равна приращению ее функции распределения, то есть
равна приращению ее функции распределения, то есть 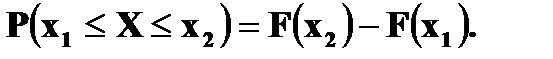
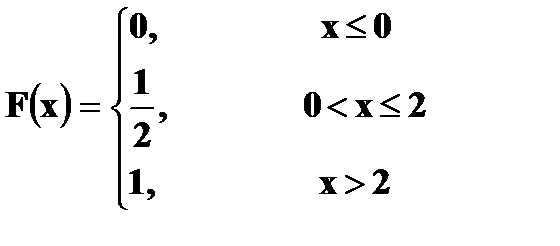
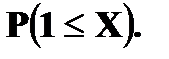
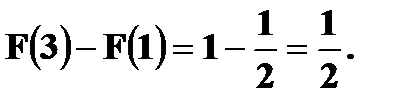
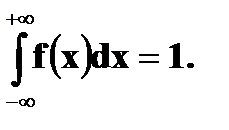
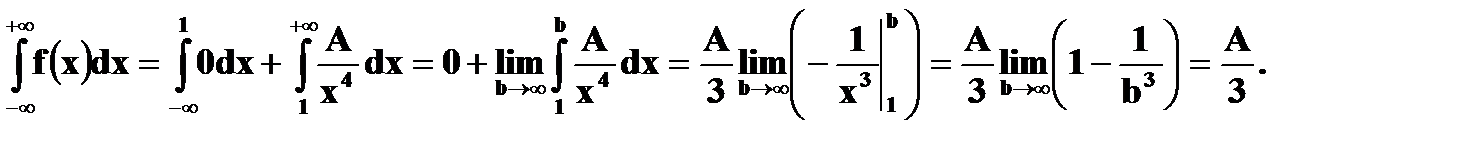
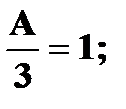 тогда
тогда 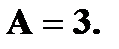
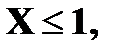 то
то 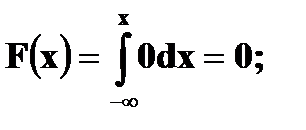
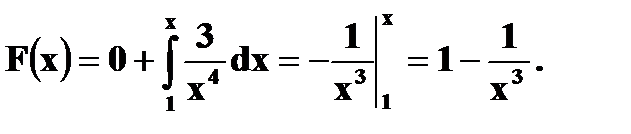
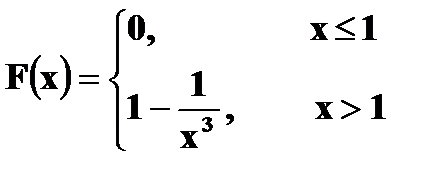
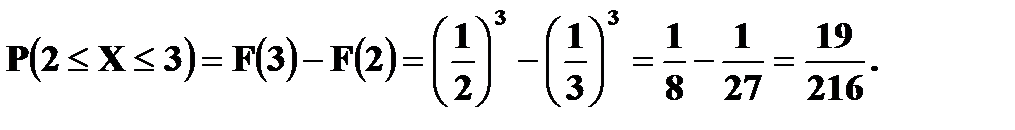
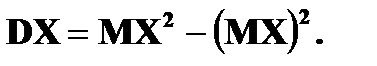
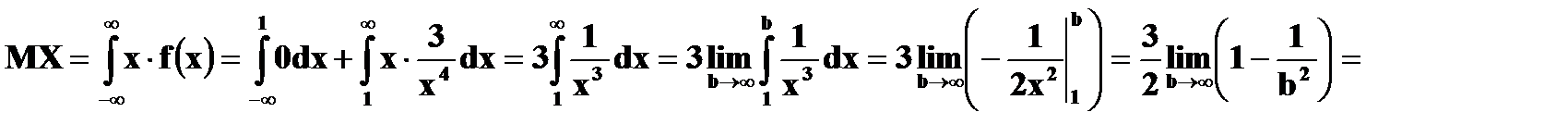
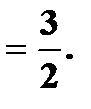
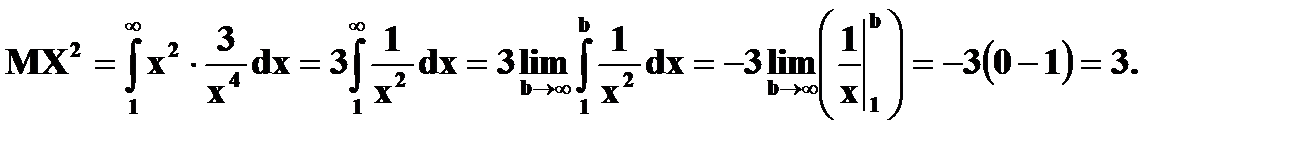
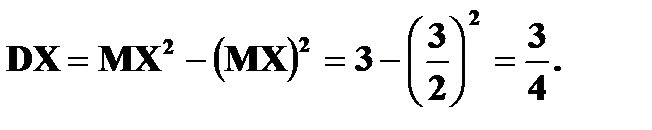
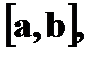 если ее плотность вероятности
если ее плотность вероятности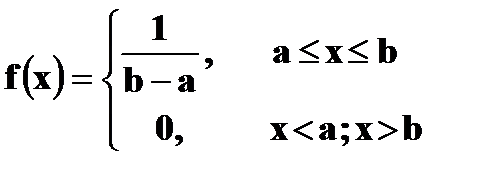
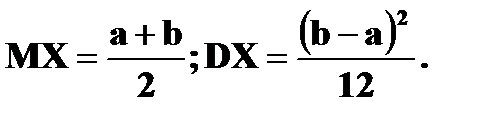
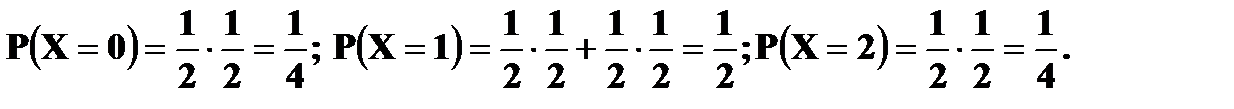
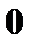
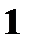
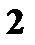
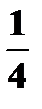
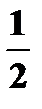
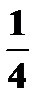
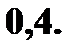 Составьте закон распределения числа вызовов, если: а) число вызовов не более 5; б) число вызовов не ограничено.
Составьте закон распределения числа вызовов, если: а) число вызовов не более 5; б) число вызовов не ограничено.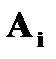 —
—  – ый вызов принят
– ый вызов принят 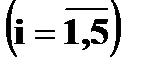 . Вероятность того, что первый вызов принят
. Вероятность того, что первый вызов принят 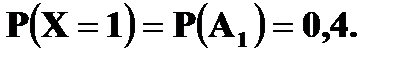 Второй вызов состоится лишь при условии, что первый вызов не будет принят, и
Второй вызов состоится лишь при условии, что первый вызов не будет принят, и 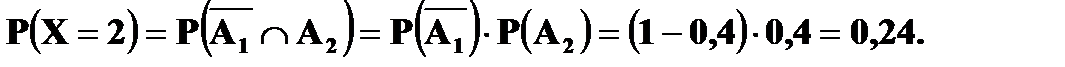
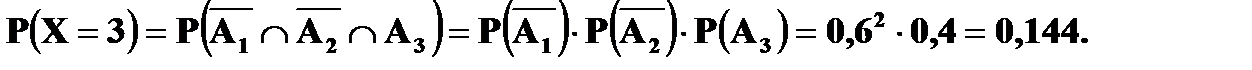
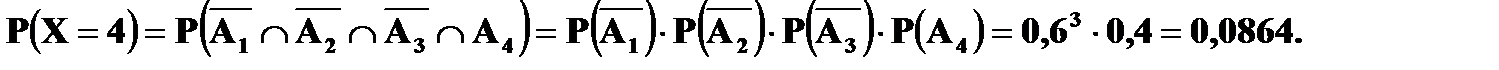
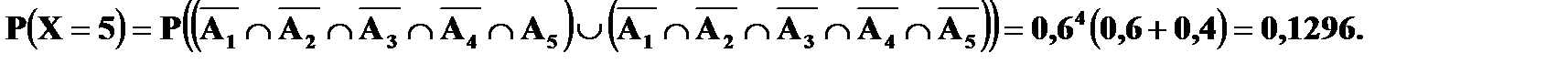
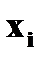

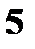
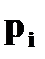
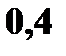
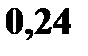
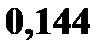
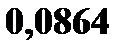
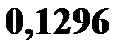
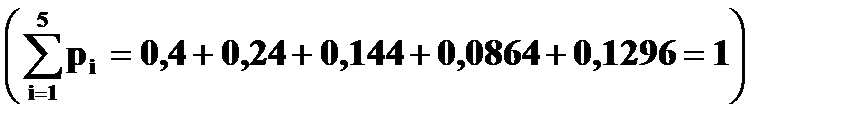
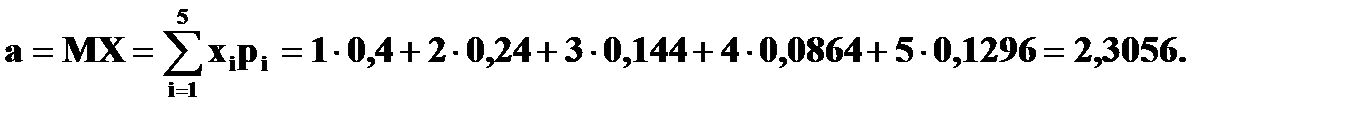
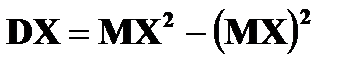
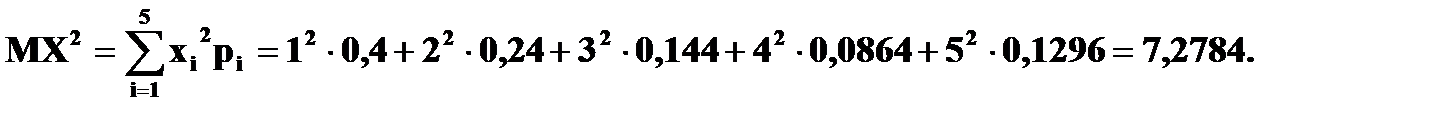
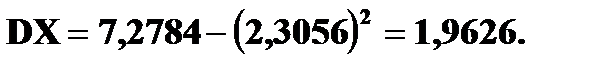
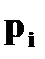
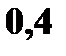
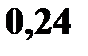
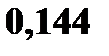
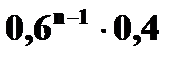
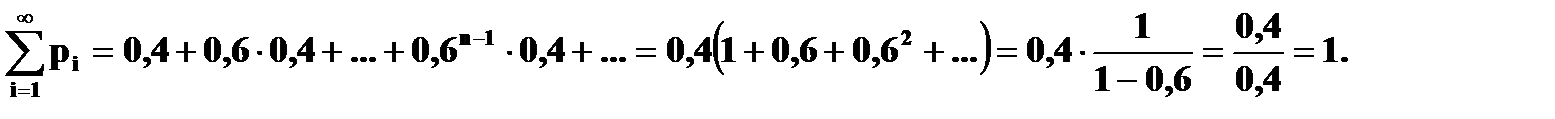
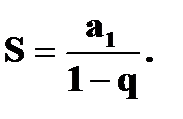 В нашем случае
В нашем случае 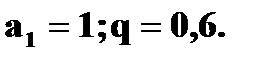
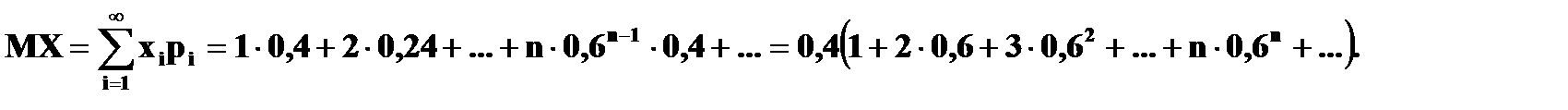
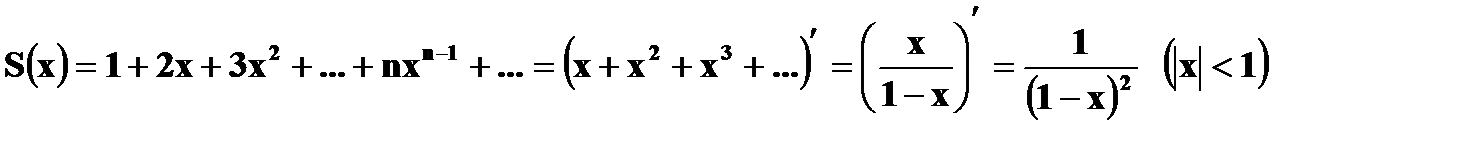
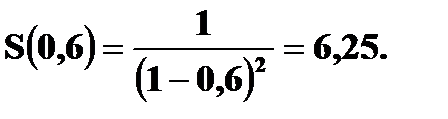
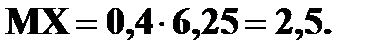
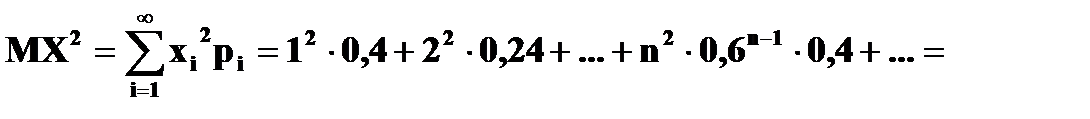
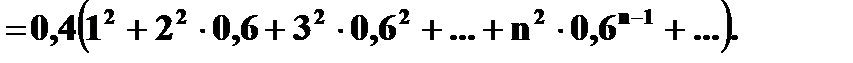
 при
при 
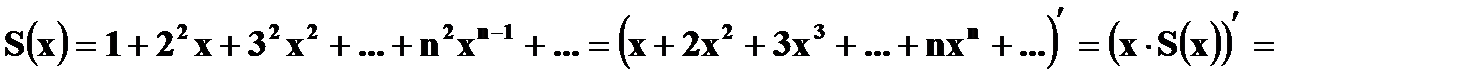
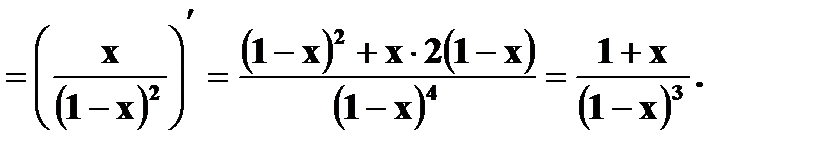
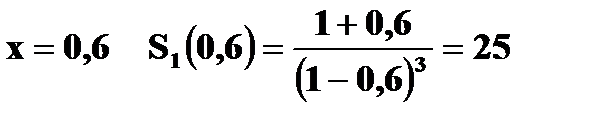
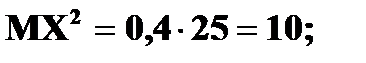
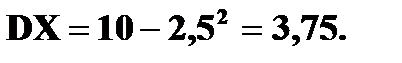
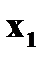 и
и 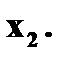 По условию одна из вероятностей равна 0,8. Пусть
По условию одна из вероятностей равна 0,8. Пусть 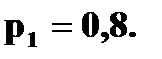 Тогда
Тогда 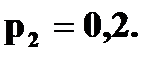 Запишем ряд распределения
Запишем ряд распределения 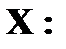
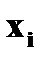
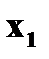
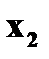
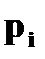
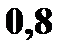
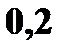
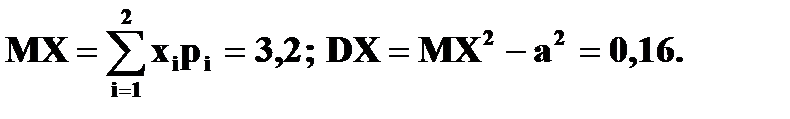
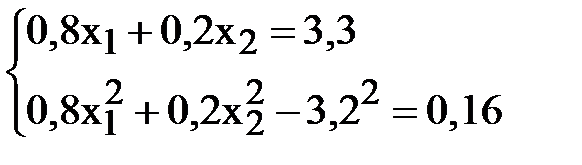
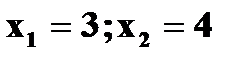 и
и 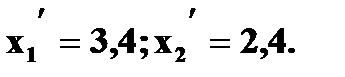
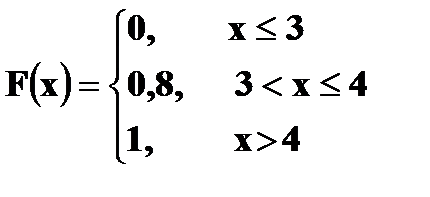 или
или 
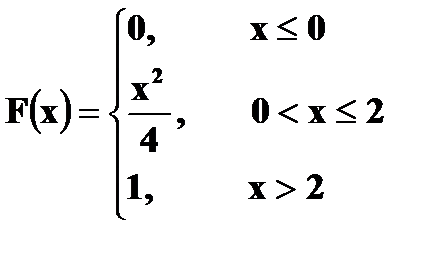
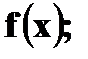
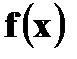 и
и 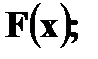
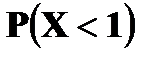 и
и 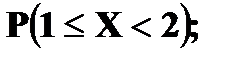
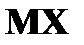 и
и 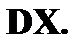
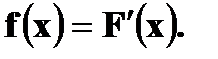
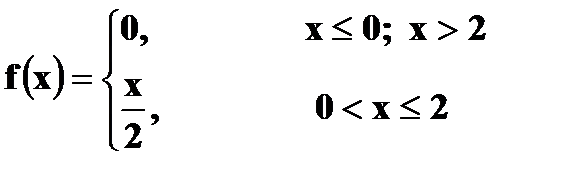

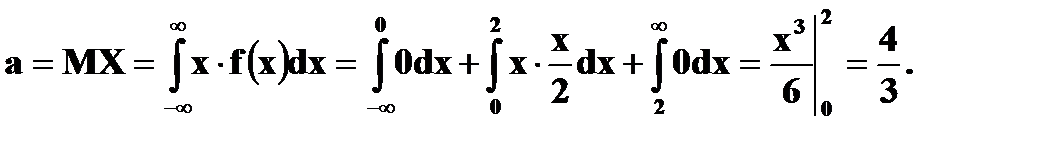
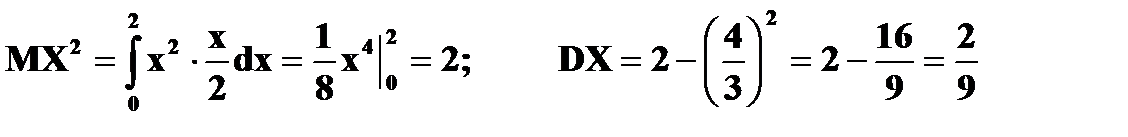
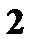
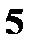
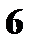
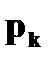
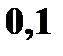
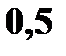
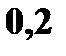
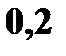
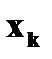
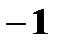
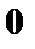
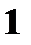
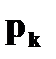
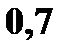
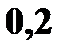
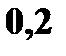
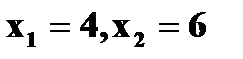 с вероятностями
с вероятностями 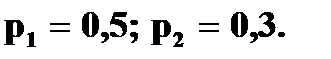 Найдите
Найдите 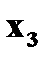 и
и 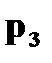 , если
, если 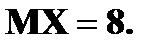
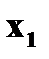 и
и 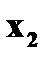 ,
, 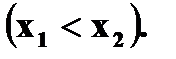
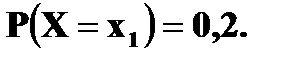 Составьте закон распределения случайной величины X, если
Составьте закон распределения случайной величины X, если 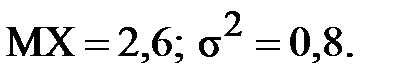 Найдите функцию распределения
Найдите функцию распределения  и постройте ее график.
и постройте ее график.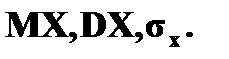
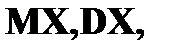 функцию распределения
функцию распределения 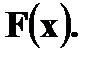 Постройте график
Постройте график 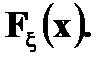 (Каждый стрелок делает по одному выстрелу).
(Каждый стрелок делает по одному выстрелу).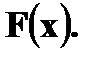 Найдите
Найдите 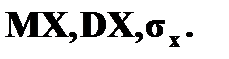
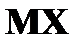 и
и 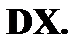
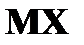 и
и 
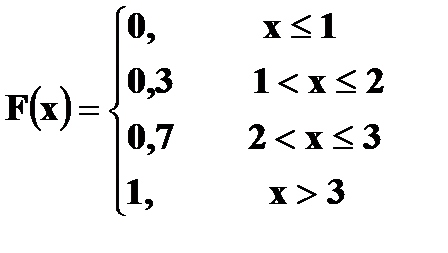
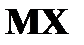 и
и 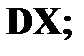 в) постройте график
в) постройте график 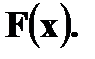
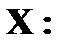
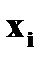
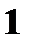
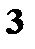
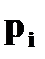

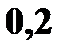
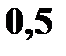
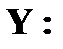
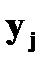
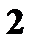
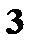
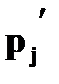
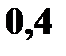
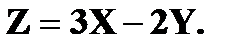 Проверьте, выполняются ли свойства
Проверьте, выполняются ли свойства 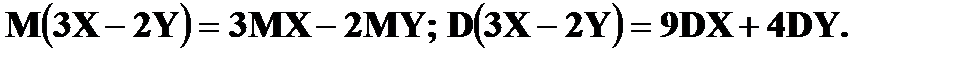
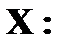
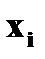
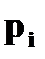
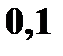
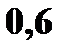
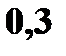
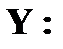
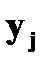
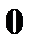
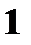
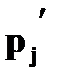
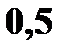
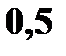
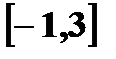 и задана функцией распределения
и задана функцией распределения 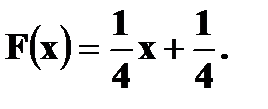 Найдите вероятность попадания случайной величины X в интервал
Найдите вероятность попадания случайной величины X в интервал 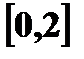 . Постройте график функции
. Постройте график функции 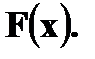
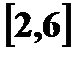 , задана функцией распределения
, задана функцией распределения 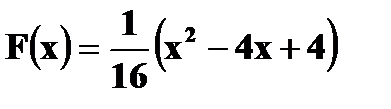 . Найдите вероятность того, что случайная величина X примет значения: а) меньше 4; б) не меньше 6; в) не меньше 3; г) Вычислите вероятность попадания случайной величины в интервал
. Найдите вероятность того, что случайная величина X примет значения: а) меньше 4; б) не меньше 6; в) не меньше 3; г) Вычислите вероятность попадания случайной величины в интервал 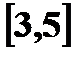 .
.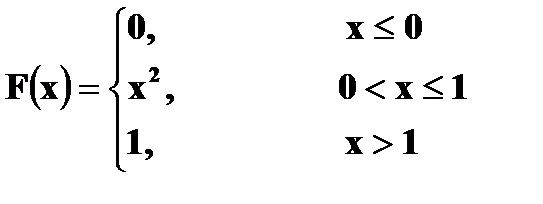
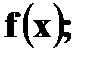
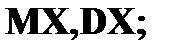
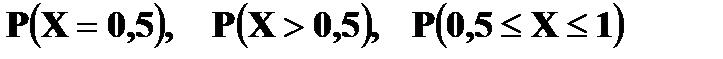 ;
;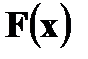 и
и 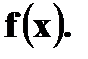
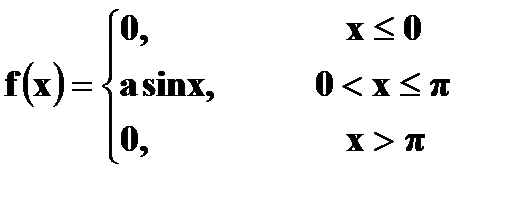
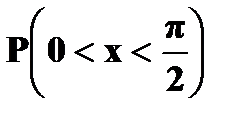 ; б)
; б) 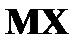 и
и 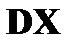 .
.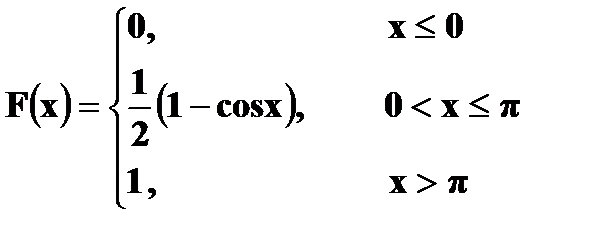
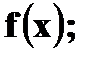 2)
2) 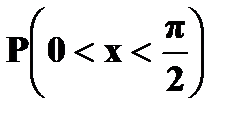
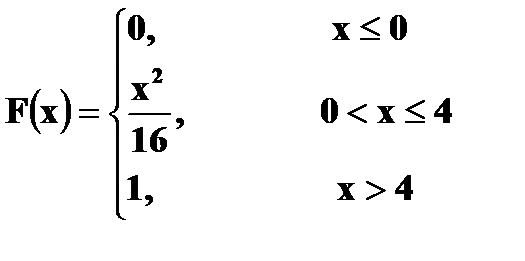
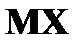 и
и 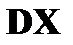 .
.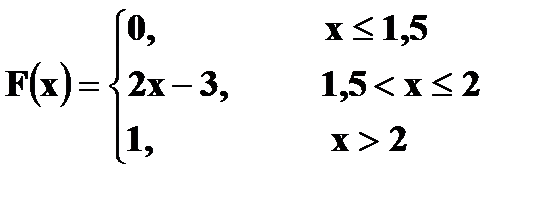
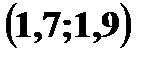 .
.