
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие математических моделей. Этапы математического моделирования систем. Декомпозиция модели. Структура модели систем.
Математическая модель – это формальная система, представляющая собой конечное собрание символов и совершенно строгих правил оперирования этими символами в совокупности с интерпретацией свойств определенного объекта некоторыми отношениями, символами или константами. Этапы моделирования системы: 1. Декомпозиция модели – одна большая система разбивается на несколько подсистем, где каждая анализируется в отдельности, при этом подсистемы должны иметь связь между собой и описываться законами физики, химии и т.д.. Если это выполняется, то строится математическая модель системы, если нет, то необходимо разбить подсистему на более мелкие подсистемы и искать связи. Если это условие не выполняется, то данная система работает по принципу “черного ящика” 2. Выбор структуры элементов модели – определение математической зависимости выходного от входного параметра, E, u, т.е. отыскание Y=f(x, u, E). Для того, чтобы ввести однозначность системы, необходимо определить P(x) – состояние системы – представляет собой уравнение состояния с учетом временного интервала, совокупности входных параметров и начальное состояние системы, т.е: P(r)=S{X0r, P(r0), [r0, r]} – уравнение состояния системы от начального момента времени до текущего S – оператор перехода 3. Композиция модели, составление уравнений связей Входной процесс, разбиваемый на участки, должен соответствовать условию однозначности. Это говорит о том, что отдельные элементы системы должны соответствовать друг другу и иметь одинаковые функциональные связи (т.е. S должна быть однозначна F) 4. Идентификация параметров модели 5. Выбор алгоритма 6. Анализ результатов Структурой модели является зависимость выхода от входа, управляющего воздействия, внешнего воздействия. Таким образом: Y(r)=F1[x1(r), u1(r), E(r)] – типичная структура модели “вход-выход”, характерная для “черного ящика” Для того, чтобы ввести однозначность (исключить неоднозначность в зависимости между входом и выходом), необходимо учитывать состояние системы: P(r)=S{x0, P(r0), [r1, r2]} – состояние системы в интервале [r1, r2] S – оператор перехода, который позволяет рассчитать параметры внутреннего состояния системы в данный момент, в зависимости от изменения исходных параметров и времени
Введенный параметр позволяет получить модель “вход-выход-состояние”: Y(r)=F{x0, P(r), [r1, r2]}, F – оператор выхода S и F должны удовлетворять свойству однозначности, которая позволяет разбивать входной процесс на произвольные сочлененные между собой участки и анализировать поведение системы на каждом участке отдельно: Разобьем интервал [r1, r2] на [r1, r0] и [r0, r2] и запишем: P(r)=S{x01, P(r0), [r1, r0]}= S{x02, P(r1), [r0, r2]}=S{x02, S{x01, P(r0), [r1, r0]}, [r0, r2]} Y(r)=F{x01, P(r0), [r1, r0]}= F{x02, P(r1), [r0, r2]}=F{x02, S{x01, P(r0), [r1, r0]}, [r0, r2]} Эти выражения и характеризуют свойство однозначности. Постановка задач математического программирования. Примеры задач. Задача шихтовки. Математическое программирование изучает теорию и методы решения задач оптимизации, т.е. нахождение экстремума целевой функции при учете ограничений. Во-первых, необходимо разработать целевую функцию: Z(x1, x2…xi…xn)->max(min) – задача без условной оптимизации Для решения задачи оптимизации необходимо разработать ограничения:
Z( Для условия hj(x1…xi…xn) gi(x1…xi…xn) В этом случае, h и g – параметры, которые формируют Нахождение максимума (минимума) – одна и та же задача. Если необходимо перейти к решению с минимума на максимум, достаточно умножить на (-1). Существуют активные и неактивные ограничения. Активные влияют на результат решения задачи, неактивные – не влияют. В случае многоэкстремальности существующие методы математического моделирования позволяют определить только такие значения переменных, которые соответствуют локальным минимумам или максимумам функции. Задача нахождения глобальных экстремумов достаточно сложна, т.к. требует их определения на некотором множестве. Задача шихтовки. Требуется найти оптимальное значения расходов x1…xn. Целевая функция Z=СУММ(ci*xi)->min (необходимо оптимально отрегулировать расход шихты для получения заданной марки стали с минимальными затратами). Полагаем, что химический состав известен. Решаем задачу линейного программирования: X1 a11 a21 C1 X2 a12 a22 C2
………………... ………………… Xi a1i a2i Ci ……………….. Xn a1n a2n Cn (С – себестоимость, b1 – содержание железа, b2 – содержание серы) a, b, c – постоянные значения Ограничения: 1. СУММ(xi) 2. a11*x1+a12*x2+…+a1n*xn 3. a21*x1+a22*x2+…+a2n*xn 4. xi>0 (расход шихты является положительным числом)
Билет 3.
|
||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.244.201 (0.009 с.) |

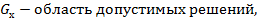

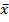 )->max(min) – задача условной оптимизации (решение задачи экстремума)
)->max(min) – задача условной оптимизации (решение задачи экстремума) имеем:
имеем: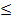 0, 1
0, 1  0, m+1
0, m+1 
 b1 (концентрация железа в металле должна соответствовать регламентируемому значению)
b1 (концентрация железа в металле должна соответствовать регламентируемому значению)


