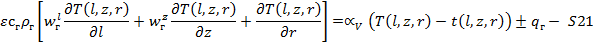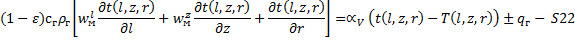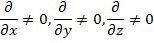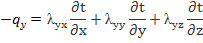Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные этапы разработки систем. Определение границ системы, входных и выходных параметров. Моделирование систем, классификация моделей систем.Стр 1 из 5Следующая ⇒
Билет 1. Постановка задачи математического программирования. Проблемы решения задач. Математическое программирование изучает теорию и методы решения задач оптимизации, т.е. нахождение экстремума целевой функции при учете ограничений. Во-первых, необходимо разработать целевую функцию: Z(x1, x2…xi…xn)->max(min) – задача без условной оптимизации Для решения задачи оптимизации необходимо разработать ограничения:
Z( Для условия hj(x1…xi…xn) gi(x1…xi…xn) В этом случае, h и g – параметры, которые формируют Нахождение максимума (минимума) – одна и та же задача. Если необходимо перейти к решению с минимума на максимум, достаточно умножить на (-1). Существуют активные и неактивные ограничения. Активные влияют на результат решения задачи, неактивные – не влияют. В случае многоэкстремальности существующие методы математического моделирования позволяют определить только такие значения переменных, которые соответствуют локальным минимумам или максимумам функции. Задача нахождения глобальных экстремумов достаточно сложна, т.к. требует их определения на некотором множестве.
Билет 2. Постановка задач математического программирования. Примеры задач. Задача шихтовки. Математическое программирование изучает теорию и методы решения задач оптимизации, т.е. нахождение экстремума целевой функции при учете ограничений. Во-первых, необходимо разработать целевую функцию: Z(x1, x2…xi…xn)->max(min) – задача без условной оптимизации Для решения задачи оптимизации необходимо разработать ограничения:
Z( Для условия hj(x1…xi…xn) gi(x1…xi…xn) В этом случае, h и g – параметры, которые формируют Нахождение максимума (минимума) – одна и та же задача. Если необходимо перейти к решению с минимума на максимум, достаточно умножить на (-1). Существуют активные и неактивные ограничения. Активные влияют на результат решения задачи, неактивные – не влияют. В случае многоэкстремальности существующие методы математического моделирования позволяют определить только такие значения переменных, которые соответствуют локальным минимумам или максимумам функции. Задача нахождения глобальных экстремумов достаточно сложна, т.к. требует их определения на некотором множестве.
Задача шихтовки. Требуется найти оптимальное значения расходов x1…xn. Целевая функция Z=СУММ(ci*xi)->min (необходимо оптимально отрегулировать расход шихты для получения заданной марки стали с минимальными затратами). Полагаем, что химический состав известен. Решаем задачу линейного программирования: X1 a11 a21 C1 X2 a12 a22 C2 ………………... ………………… Xi a1i a2i Ci ……………….. Xn a1n a2n Cn (С – себестоимость, b1 – содержание железа, b2 – содержание серы) a, b, c – постоянные значения Ограничения: 1. СУММ(xi) 2. a11*x1+a12*x2+…+a1n*xn 3. a21*x1+a22*x2+…+a2n*xn 4. xi>0 (расход шихты является положительным числом)
Билет 3. Билет 4. Билет 5 Билет 6. 1. Примеры моделирования систем в металлургии на примере шахтной печи металлизации. В шахтной печи металлизации соблюдается противоточная схема движения. Построим модель в 2-мерной системе координат (L, z). Состав шихтовых материалов – Fe2O3, Fe3O4, CaO, SiO2 и т.д. Состав дымовых газов – CO, H2, N… X(r)={состав газов, состав шихты, t(r), Vг(r)} Y(r)={состав полученных материалов, состав отходящих газов, производительность агрегата, tм, tг} P(r)={температурное поле материала и газа по L и r, скорость движения газов и материала, степень восстановления} Tг=f(l, z, r), Tм=f(l, z, r), wм=f(l, z, r), wг=f(l, z, r), СМ=СГ=f(l, z, r) Воспользуемся принципом декомпозиции: S0=S1+S2+S3+S4 S1: СМ=СГ=f(l, z, r) – подсистема физико-химических превращений S2: Tг=f(l, z, r), Tм=f(l, z, r) – подсистема теплообмена S3: wг=f(l, z, r) – подсистема газодинамики S4: wм=f(l, z, r) – подсистема движения материалов Рассмотрим S2 и S4: Ограничения: нагрев термически тонких тел, конвективный теплообмен в рабочем пространстве, потери тепла через кладку минимальны.
Закон сохранения энергии:
Граничные условия: 1) Модель динамическая 2) Модель двумерная с распределенными параметрами (изменение параметров по пространственным координатам) 3) Модель нелинейная Движение газов и материалов в среде линейно и описывается уравнением Навье-Стокса. 4) Модель детерминированная S4: Будем считать, что состояние системы отсутствует P(r)=0, таким образом, прибегнем с принципу “черного ящика” (материал слоями движется параллельно вниз). Скорость газов равна нулю. Согласно уравнению неразрывности:
Билет 7 1. Примеры моделирования систем на примере машины непрерывного литья заготовок. Билет 8 Билет 10 Распределенность и сосредоточенность математических моделей систем. Примеры. В моделях с распределенными параметрами учитывается неравномерность распределенных параметров внутреннего состояния, выходных параметров по пространственным координатам. Признаком того, что модель является таковой, является наличие частных производных по пространственным координатам параметров объекта, т.е.:
Примерной такой модели может быть уравнение Фурье:
Модель с сосредоточенными параметрами – это модель системы, которая описывается обыкновенными дифференциальными уравнениями. Все параметры в уравнении зависят только от времени. Типичным примером такой модели является дифференциальное уравнение ускорения (a=dV/dt). Билет 11 Билет 12 Билет 13 Билет 14 Линейные системы управления и описание их в виде модели Вход-выход. Линеаризация нелинейных дифференциальных уравнений систем управления. Принцип малых отклонений. Стандартная форма записи линеаризованного уравнения. Физический смысл коэффициентов уравнения. Область применения линеаризованных моделей. Примеры реализации. Определим линейность такой модели: на заданном интервале [r1, r2] два фрагмента выходного параметра x1 и x2, а в один и тот же начальный момент два различных начальных состояния, следовательно: P1(r)=S{x01, P1(r0), [r1, r2]} P2(r)=S{x02, P2(r0), [r1, r2]} Y1(r)=F{x01, P1(r0), [r1, r2]} Y1(r)=F{x02, P2(r0), [r1, r2]} Определяющим фактором линейной модели является однородность и аддитивность S и F. Свойство однородности: F{kx1, kP(r0), [r1, r2]}=kF{x1, P(r0), [r1, r2]} S{kx1, kP(r0), [r1, r2]}=kS{x1, P(r0), [r1, r2]} Свойство аддитивности: F{x0, P(r0), [r1, r2]}= F{x1, P1(r0), [r1, r2]}+ F{x2, P2(r0), [r1, r2]} (Y(r)=Y1(r)+Y2(r)) S{x0, P(r0), [r1, r2]}= S{x1, P1(r0), [r1, r2]}+ S{x2, P2(r0), [r1, r2]} (P(r)=P1(r)+P2(r)) Операторы S и F являются линейными, если они одновременно соответствуют свойствам однородности и аддитивности. Система линейна, если эти операторы линейны. Основное свойство линейности – использования принципа суперпозиции, т.е. на функциональном временном интервале реакция системы на сумму входных воздействий и начальных состояний равна сумме этих реакций от этих входных процессов и начальных состояний в отдельности. Если xo=СУММ(xi0) и P(r0)=СУММ(Pi(r0)), то Y(r)=СУММ(Yi(r)) и P(r)=СУММ(Pi(r)). Принцип малых отклонений описан в другом билете. Стандартная форма записи линеаризованных уравнений. Линеаризованное дифференциальное уравнение записывается так, чтобы выходные величины и её производные находились в левой части уравнения, а входные – в правой, при этом сама выходная величина входила в уравнение с коэффициентом единица.
Отбросив слагаемые высокого порядка ввиду их малой значимости, имеем:
K – коэффициент передачи (характеризует изменение выходного параметра относительно входного в стационарном установившемся состоянии), Т – мера инерции объекта (характеризует скорость изменения выходного параметра по изменению входного) В преобразовании по Лапласу получим:
Область применения линеаризованных уравнений. В металлургии большинство процессов описываются нелинейными дифференциальными уравнениями. Для их упрощения применяется линеаризация. В качестве примера можно привести моделирования уровня расплава на МНЛЗ (см. выше) – там происходит линеаризация закона сохранения масс в различных подсистемах. Об остальном выше! Билет 15 Билет 16 Билет 1. Основные этапы разработки систем. Определение границ системы, входных и выходных параметров. Моделирование систем, классификация моделей систем. Под системой подразумевается совокупность объектов, которые обладают некоторыми свойствами, характеристиками, могут изменяться как во времени, так и в пространстве под влиянием взаимодействия других элементов системы. Для моделирования процессов и объектов в металлургии используется система SCADA – система управления технологическими агрегатами. Для того, чтобы разрабатывать и пользоваться системой, необходимо: 1) Понимать процесс 2) В полной мере пользоваться информацией об изменении управляющего воздействия u(x) и y(x). Знание такой информации упрощает моделирование. Отсутствие понимания того, как изменяется одна величина относительно другой, делает разработку практически невыполнимой 3) Вести разработку системы с учетом фактора времени (все процессы должны работать в режиме реального времени) 4) Наложить ограничения на систему. Без ограничений невозможно добиться точного результата, система выдаст бесконечное множество решений. Для теплообмена в агрегатах необходимо создать граничные условия (граничные условия 1-го, 2-го, 3-го и 4-го рода) 5) Учесть то, что система динамическая (все параметры изменяются по времени) Таким образом, этапы разработки системы: 1) Формулировка цели Z разработки системы – количественный показатель, характеризующий качество системы. Является основополагающим этапом (должна быть четко сформулирована цель, четкая ориентированность, ее важность) 2) Определение границ системы, входных и выходных параметров x, u, y, u
3) Моделирование системы В качестве модели принимается выходная величина: Y(r)=F[x(r), u(r), E(r), r] 4) Синтез управления – необходимо разработать план управления u(r) для достижения Z с использовании информации о x(r), u(r), E(r), Y(r). 5) Коррекция – определяет возврат к предыдущим этапам с целью учета границ раздела системы, т.к. система “эволюционирует” (изменяется по времени, поэтому необходима постоянная корректировка) Определение границ системы основывается на создании границ, которые бы создавали минимум связей с внешней средой, а также создании управляемости, т.е. достижения поставленной цели. Предпочтительней система, в которой есть возможность управлять x(r) (неконтролируемая величина, за счет связи с внешней средой), однако такой подход вводит в систему дополнительные неконтролируемые возмущения E(r) Модель системы с одиночным E(r) c одной функциональной связью: Y(r)=F1[x1(r), u1(r), E(r), r] Модель системы с несколькими E(r) и множеством функциональных связей: Y(r)=F1[F2[x2(r), u2(r), E2(r), r]x1(r), u1(r), E1(r), r] – предпочтительней, более сложная, но дает точный результат Выбор входных и выходных параметров заканчивается выделением системы из внешней среды, т.е. созданием границ системы. Методы моделирования системы: 1. Метод “черного ящика” – подразумевает анализ системы без оглубления в физику процесса. В металлургических процессах не очень эффективен, поскольку в лучшем случае он применим только для конкретных систем без возможности переноса на другие однотипные системы. При этом нет однозначной функциональной зависимости между входом и выходом, т.к. внутренние свойства объекта во времени могут изменяться. 2. Аналитический подход – подразумевает наличие физики процесса, входные и выходные параметры связываются зависимостями Этапы моделирования системы: 1. Декомпозиция модели – одна большая система разбивается на несколько подсистем, где каждая анализируется в отдельности, при этом подсистемы должны иметь связь между собой и описываться законами физики, химии и т.д.. Если это выполняется, то строится математическая модель системы, если нет, то необходимо разбить подсистему на более мелкие подсистемы и искать связи. Если это условие не выполняется, то данная система работает по принципу “черного ящика” 2. Выбор структуры элементов модели – определение математической зависимости выходного от входного параметра, E, u, т.е. отыскание Y=f(x, u, E). Для того, чтобы ввести однозначность системы, необходимо определить P(x) – состояние системы – представляет собой уравнение состояния с учетом временного интервала, совокупности входных параметров и начальное состояние системы, т.е: P(r)=S{X0r, P(r0), [r0, r]} – уравнение состояния системы от начального момента времени до текущего S – оператор перехода 3. Композиция модели, составление уравнений связей Входной процесс, разбиваемый на участки, должен соответствовать условию однозначности. Это говорит о том, что отдельные элементы системы должны соответствовать друг другу и иметь одинаковые функциональные связи (т.е. S должна быть однозначна F)
4. Идентификация параметров модели 5. Выбор алгоритма 6. Анализ результатов
Классификация системных моделей. Выражение модели функционирования элементов системы: MF=<X, P, Y, S, F, [r1, r2]> - общесистемная модель Она определяет наличие входных и выходных параметров в системе, их функциональную зависимости через F, состояния системы, какие элементы будут включены в нее и иметь с ней зависимость через S, и все это будет существовать в установленном интервале времени функционирования системной модели [r1, r2]. 1) Стационарные – сдвиг по времени не влияет на свойства объекта, здесь MF=<X, P, Y, S, F> 2) Нестационарные – сдвиг по времени влияет на объект, выходные параметры сдвигаются по времени и могут изменять свою форму 3) Линейные – описываются линейными операторами S и F (они линейны, если подчиняются правилам аддитивности и однородности) 4) Нелинейные – обратное 5) Детерминированные Для детерминированных моделей математические уравнения должны однозначно определять состояния системы и выходные параметры в данный момент времени через фрагменты выходного процесса и параметры состояния в начальный момент времени. 6) Стохастические В стохастических моделях предполагается наличие неконтролируемых факторов как на входе, так и внутри самой системы, вносящие неопределенность в систему. Неопределенность вызывается изменением состояния системы и наличием внешних возмущений. Для описания такой вводится случайный оператор P(r)=S”{X0, Ex(r), P(r0, E0), [r0,r]} Y(r)=F”{P(r), Ey(r), [r0,r]} 7) Непрерывные 8) Дискретные 9) Сосредоточенные 10) С распределенными параметрами 11) Одномерные 12) Многомерные
|
|||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.228.95 (0.07 с.) |

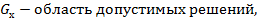

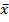 )->max(min) – задача условной оптимизации (решение задачи экстремума)
)->max(min) – задача условной оптимизации (решение задачи экстремума) имеем:
имеем: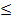 0, 1
0, 1  0, m+1
0, m+1 
 b1 (концентрация железа в металле должна соответствовать регламентируемому значению)
b1 (концентрация железа в металле должна соответствовать регламентируемому значению)