По каким признакам классифицируются фермы.

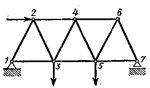
1. По размерности: плоские; пространственные.

2. По назначению: перекрытие пролетов; мостовые; башенные; крановые.

3. По опиранию: балочные, консольные, консольно-балочные, распорные.

4. По сложности: простые; шпренгельные; вантовые.

5. По очертанию: с параллельными поясами; трапецеидальные; треугольные; полигональные.

6. По типу решетки: раскосные; полураскосные; ромбические и тд.

108. Классификация ферм по опиранию (положению опор)?

1. Балочные:

1.1. Бесконсольные

1.2. Консольно-балочные

1.3. Консольные

2. Распорные

109. Классификация ферм по очертанию поясов?

1. С параллельными поясами

2. Треугольные

3. Трапецеидальные

4. С полигональными поясами:

· параболическими

· эллиптическими

· круговыми

110. Классификация ферм по типу решетки?

1. Раскосные

2. С треугольной решеткой

3. Полураскосные

4. Многораскосные

5. Многорешётчатые

111. ​ Какие фермы принято называть простыми?

Простые фермы – плоские фермы, образованные добавлением к базовому треугольнику 1-2-3 каждого из последующих треугольников присоединением двух не лежащих на одной прямой стержней и одного узла. Взаимные смещения узлов в такой ферме невозможны.

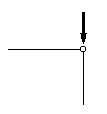
112. Какие внутренние усилия возникают в ферме, правило знаков?

В стержнях фермы возникают только продольные внутренние усилия, а именно растяжение или сжатие. Согласно принятому правилу знаков: растягивающие усилия положительны, а сжимающие – отрицательны.

113. Какие стержни фермы называются нулевыми, их признаки?

Нулевым стержнем называется стержень, в котором при рассматриваемой нагрузке усилие равно нулю. Приведем его признаки:

1. Если в незагруженном узле под углом соединяются два стержня, то оба стержня - нулевые (рис.7.24). В этом легко убедиться, составив уравнения проекций сил на оси, совпадающие с направлением стержней.

2. Если в незагруженном узле сходятся сходятся три стержня, причем два лежат на одной прямой, то третий стержень - нулевой (рис.7.25). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную двум стержням, лежащим на одной прямой.

3. Если к узлу, в котором сходятся два стержня, приложена сила, направление действия которой совпадает с одним из них, то второй стержень - нулевой (рис.7.26). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную линии действия внешней силы.

Рис. 7.24 Рис. 7.25 Рис. 7.26

4. Если в узле сходятся три и более стержней, то те из них, о которых заранее известно, что они являются нулевыми, при определении остальных нулевых стержней и нахождении усилий в стержнях, очевидно, могут быть мысленно отброшены.

5. Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.

114. ​ Способы расчета усилий в стержнях стат. определимых ферм?

1. Аналитический:

1.1. Способ вырезания узлов

1.2. Способ сквозных сечений

2. Графический (с помощью диаграммы Максвелла-Кремоны)

115. ​ В чем состоит идея способа вырезания узлов?

При вырезании узла мы получаем плоскую систему сходящихся сил, которая должна удовлетворять двум уравнениям равновесия.

При использовании данного способа неизвестные усилия в стержнях фермы, сходящийся в узле, направляют от узла, задаваясь их положительным значением (растяжением). Если в результате получается отрицательное значение – стержень сжат.

Последовательность рассмотрения узлов должна быть такая, чтобы каждый последующий узел содержал не более двух неизвестных усилий.

Недостатки способа: громоздкость и невозможность определений усилий в последующих стержнях без определения усилий в предыдущих.

116. ​ Какие условия применимости способа вырезания узлов?

Методом вырезания узлов целесообразно пользоваться при определении усилий в стержнях простых ферм, которые могут быть образованы последовательным присоединением узлов. Исследование геометрической неизменяемости подобных ферм удобно проводить методом разрушения, снимая последовательно узлы, прикреплённые минимально необходимым числом правильно ориентированных стержней. В таком же порядке следует обходить узлы и при определении усилий в стержнях. Тогда для каждого узла количество неизвестных усилий будет равно числу уравнений равновесия. Если при этом ферма свободная и находится на опорах, то целесообразно предварительно определить опорные реакции.

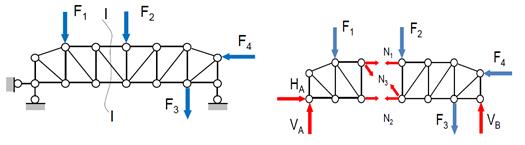
117. Какие уравнения равновесия составляют при вырезании узла?

Уравнения равенства нулю суммы проекций всех сил на вертикальную и горизонтальную оси Σ X =0 и Σ Y =0.

118. В чем состоит идея способа сквозных сечений?

Способ сечений позволяет определять усилия во многих стержнях фермы независимо от того, известны ли усилия в других стержнях.

Плоская ферма разрезается на две части таким образом, чтобы в сечение попали три стержня. Действие одной части на другую заменяется неизвестными усилиями в стержнях. Уравнения равновесия представляются в виде равенства нулю моментов всех сил относительно точек пересечения направлений каждой пары стержней, попавших в сечение. Если два из попавших в сечение стержней параллельны, то одно из уравнений моментов заменяется суммой проекций всех сил на ось, перпендикулярную направлению этих стержней.

Преимущество метода моментных точек заключается в том, что каждое уравнение равновесия содержит только одно неизвестное усилие.

119. Какие условия применимости способа сквозных сечений?

Проведенное сечение (рассечённая панель) должно содержать не более трёх неизвестных усилий.

120. Какие уравнения равновесия используются в способе сечений?

Уравнения равновесия представляются в виде равенства нулю моментов всех сил относительно точек пересечения направлений каждой пары стержней, попавших в сечение. Если два из попавших в сечение стержней параллельны, то одно из уравнений моментов заменяется суммой проекций всех сил на ось, перпендикулярную направлению этих стержней (ΣМ1=0, ΣМ2=0, Σ X =0 (Σ Y =0)).