
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование разностных уравнений
Цель работы:ознакомиться с методикой моделирования разностных уравнений с помощью пакета MATLAB и SIMULINK.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Линейное однородное разностное уравнение второго порядка с постоянными коэффициентами имеет вид:
Чтобы подчеркнуть дискретный характер изменения времени, это уравнение часто записывают в форме
Разностные уравнения третьего и более высоких порядков записываются аналогично. Известны два основных метода решения линейных разностных уравнений – с помощью характеристического полинома и с использованием z -преобразования, аналогичного преобразованию Лапласа.
1.1. Решение разностных уравнений с помощью характеристического полинома Будем искать решение однородного разностного уравнения в виде x (t)= zt, где z – некоторое число. Подставляя x (t) в разностное уравнение (1) при f (t)=0 и сокращая на zt, получаем характеристическое уравнение
Если его корни z 1, z2 вещественные и различные, то общее решение имеет вид:
Если z 1= z2,, то в решении появляется линейный множитель
В случае пары комплексно-сопряженных корней z 1,2= a ± i b решение может быть записано в вещественной форме
Здесь r – модуль комплексного числа z 1, а j – его аргумент. Формулы для уравнений более высоких порядков выглядят так же, просто увеличивается число слагаемых в решении. Пример 1. Решим разностное уравнение x (t +2) –5 x (t +1) + 6 x (t) = 0. Характеристическое уравнение имеет вид z 2 –5 z + 6 = 0. Его корни вещественные и различные: z 1 = 3, z 2 = 2. Общее решение: x (t) = c 1 3 t + c 2 2 t. Пример 2. Решим разностное уравнение x (t +2) + 2 x (t +1) + 4 x (t) = 0. Характеристическое уравнение: z 2 + 2 z + 4 = 0. У него комплексные корни:
Модуль и аргумент корней можно найти непосредственно на рис.1: Общее решение: Произвольные постоянные ci находят, задавая начальные условия. Пусть, например, в примере 2 заданы начальные условия x (0)=2; x (1)= –4. Записываем общее решение для t =0 и t =1:
Отсюда находим с1 =2, с 2=0. Следовательно, решение имеет вид Общее решение неоднородного разностного уравнения представляет собой сумму общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения. Частное решение ищут в том же виде, что и правая часть, т.е. функция f (t) в уравнении (1):
– если f (t) – постоянная, то в виде константы; – если f (t) – экспонента, то в виде экспоненты с тем же показателем; – если f (t) =sin kt или cos kt, то в виде c 1sin kt + c 2cos kt. Коэффициенты с 1 и с 2 находят, подставляя частные решения в разностное уравнение и приравнивая одноименные функции справа и слева. Пример 3. Дано неоднородное разностное уравнение второго порядка
Находим корни характеристического полинома
Частное решение ищем в виде x част= c. Подставляя его в исходное уравнение, находим, что x част=2. Общее решение неоднородного уравнения получаем как сумму частного решения и общего решения соответствующего однородного уравнения
Коэффициенты с 1, с 2 находим из уравнений
1.2. Решение разностных уравнений с помощью z-преобразования При описании дискретных систем и решении разностных уравнений широко применяется аппарат z -преобразования – это дискретный аналог преобразования Лапласа. Например, умножение изображения F (p) на оператор Лапласа p соответствует дифференцированию непрерывной функции f (t). Умножение изображения F (z) на оператор z соответствует сдвигу функции f (t) (которая может быть непрерывной, дискретной или решетчатой) на один такт. Таким образом, если операторы р и 1/ р – это операторы дифференцирования и интегрирования, то операторы z и z -1 – это операторы сдвига влево и вправо. С инженерной точки зрения оператор z -1 представляет собой элемент задержки. Существуют также определенные параллели между изображениями функций F (p) и F (z). Например, изображению по Лапласу F (p) = 1 соответствует дельта-функция f (t) = d (t), а изображению F (z) = 1, соответствует единичный импульс. В том и другом случае оригиналом является элементарное импульсное воздействие. Краткая таблица z -преобразований других функций приведена в Приложении. Пусть дано разностное уравнение n -го порядка
y (t+n)+ an -1 y (t+n –1)+... + a 0 y (t)= f (t) (2)
с начальными условиями y (0)= y 0; y (1)= y 1;...; y (n –1)= yn - 1. Алгоритм его решения с помощью z -преобразования содержит 4 шага. Шаг 1. Применить z -преобразование к уравнению (2), заменяя f (t) на F (z), y (t) на Y (z); y (t +1) на z (Y (z)– y 0) и т.д. Шаг 2. Из полученного алгебраического уравнения выразить Y (z). Шаг 3. Выполнить разложение Y (z) на простые дроби. Шаг 4. Пользуясь таблицей, выполнить обратное z -преобразование. Результатом будет искомое решение разностного уравнения. Пример 4. Требуется решить разностное уравнение второго порядка
yn +2 –5 yn +1+6 yn = un
с нулевыми начальными значениями y 0, y 1и входным сигналом un =1. Шаг 1. Применяем к нему z -преобразование
Шаг 2. Выражаем Y (z) и подставляем
Шаг 3. Представляем правую часть в виде суммы простых дробей с переменной z в числителе:
В отчете разложение делается методом неопределенных коэффициентов. В пакете MATLAB это можно сделать с помощью команды residue. Шаг 4. С помощью таблицы z -преобразований или команды i ztrans тулбокса SYMBOLIC пакета MATLAB находим оригиналы каждого из слагаемых и складываем их: yn =0,5–2 n +0,5×3 n.
1.3. Система линейных разностных уравнений Матричная запись системы линейных однородных разностных уравнений имеет вид
X(t +1)=AX(t), X(0)=X0, (3)
где Решение этой системы может быть записано в компактной степенной форме X(t)=A t X0. (4) При работе в пакете MATLAB этот способ удобнее всего. Пример 5. Найдем решение системы разностных уравнений второго порядка
x (t +1) = 2 x (t), y (t +1) = –2 x (t) +2 y (t), если Матричное описание задачи имеет вид X(t +1)=AX(t),
Для получения решения воспользуемся степенной формулой. Последовательно возводя матрицу А в степени 2, 3,..., n (проделайте это!), находим
A n = 2 n
Переходя к скалярной форме записи, получаем окончательный ответ x = 2 t, y = (20– t) 2 t . Другой путь решения этой задачи связан с переходом от системы двух разностных уравнений первого порядка к одному уравнению второго порядка относительно y: y (t +2) – 4 y (t +1) + 4 y (t) = 0.
Оно получается, если выразить из второго уравнения x (t), x (t +1) и подставить в первое.
1.4. Моделирование дискретных систем в MATLAB и SIMULINK В MATLAB при моделировании линейных системы с дискретным временем используются разностные уравнения, модели в пространстве состояний и дискретные передаточные функции. В ядре MATLAB имеется команда filter, позволяющая рассчитать выходной сигнал фильтра по известному входному сигналу, заданному массивом своих значений. Ее входными аргументами являются векторы а и b коэффициентов разностного уравнения, а также массив значений сигнала и: y=filter(b,a,u). С помощью четвертого входного аргумента можно задавать начальные условия фильтра. Дискретная система в пространстве состояний, как и непрерывная система, задается четверкой матриц:
Здесь
Дискретной передаточной функцией линейной системы (5) называется отношение z -преобразования выходного сигнала к z -преобразованию входного сигнала при нулевых начальных условиях Q(z) = Y(z)/U(z). Для систем с одним входом и одним выходом она представляет собой отношение двух полиномов
Дискретная передаточная функция системы, заданной описанием в пространстве состояний (5), может быть найдена по формуле Q(z)=C(z E-A)–1B+D. Дискретные модели в MATLAB задаются при помощи тех же конструкторов ss, tf и zpk, что и непрерывные с той разницей, что последним параметром задается частота дискретизации ts(sampling time). Пример 6. Рассмотрим дискретную систему, описываемую уравнениями
при шаге дискретизации, равном 1. Создадим соответствующую ss-модель с дискретным временем:
>> a=[-1 -1/2;1/2 -1]; b=[1;0]; c=[0 1]; d=0; ts=1.0; s1=ss(a,b,c,d, ts).
На дисплей будут выведены матрицы:
и сообщение: Sampling time: 1.0 Discrete-time model.
Аналогично создаются tf и zpk-модели с дискретным временем. Обращение к полям дискретной модели осуществляется так же, как и у непрерывной, например для вывода матрицы c надо набрать код s1.c. Время дискретизации хранится в поле ts. Для моделирования дискретных систем используются те же команды (step, impulse, initial, lsim), что и в непрерывном случае. При получении весовой функции дискретных систем вместо реакции на дельта-функцию рассматривают реакцию на единичный импульс вида В тулбоксе SYMBOLIC имеются команды ztrans и i ztrans для выполнения прямого и обратного z –преобразований. Пример. Дискретная система задана уравнениями
Найдем двумя способами (символьным и численным) передаточную функцию от входа u до выхода у. В данном случае имеем следующие матрицы описания в пространстве состояний
Символьный способ. Дискретную передаточную функцию получаем по формуле Q=C(z E-A)–1B: >>syms z; >>А=[0 1;-6 5];В=[0; 7];С=[0 1]; %ввод матриц >>Q=С*inv(z*eye(2)-А))*В %передаточная функция Q=7*z/(z^2-5*z+6), %результат
Численный способ. Используем команды тулбокса CONTROL: >> A=[0 1;-6 5];B=[0; 7];C=[0 1]; >>sd=ss(A,B,C,0,1); % Discrete-time model Sampling time: 1,. >> s=tf(sd)
В обоих случаях получаем одинаковый результат:
Моделирование дискретных систем в SIMULINK производится так же, как и непрерывных. На рисунке приведены основные блоки из библиотеки Discrete.
Блок задержки Unit delay позволяет строить схемы моделирования методом Кельвина. Блоки Discrete Transfer Fcn (дискретная передаточная функция) и Discrete Filter (дискретный фильтр) определяют рациональную функцию отношения полиномов от оператора z и обратного оператора
ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
Работа состоит из двух частей. 1. В первой части исследуется дискретная система, заданная разностным уравнением yn +2 + byn +1 + ayn = un с нулевыми начальными условиями y 0=0; y 1=0. Требуется для своего варианта найти тремя способами ее реакцию на входной сигнал un =1: · последовательно рассчитав точки y 2, …, y 5; · решив разностное уравнение; · используя z -преобразование. Привести все числовые выкладки по решению разностного уравнения, дискретную передаточную функцию, ее разложение на простые дроби, график yn, схему моделирования разностного уравнения в SIMULINK, построенную на элементах задержки 1/ z и программы для вычисления в MATLAB. 2. Во второй части работы рассматривается популяция (рыб, животных), разбитых на три возрастные группы – младшего, среднего и старшего возрастов. Заданы величины р 1, р 2 – вероятности дожития особями каждой возрастной группы до следующего возраста, и числа а 1, а 2, а 3, характеризующие среднюю плодовитость каждой возрастной группы. Нужно выяснить, как изменяется со временем численность возрастных групп, и каково будет их процентное соотношение через достаточно большое время. Возрастная структура популяции описывается матричным уравнением
где x, y, z – численности трех возрастных групп. Требуется рассчитать численности возрастных групп для n = 1, 2, 3 при начальных условиях x 0= y 0= z 0=10. Теоретически найти процентное соотношение численностей x, y, z для больших n – оно определяется соотношением компонент главного собственного вектора матрицы А. Отчет должен содержать все необходимые расчеты, программы для вычисления в MATLAB и схемы моделирования в SIMULINK. Для определения собственных векторов матрицы А можно использовать символьный вариант команды e ig. ПОРЯДОК ВЫПОЛНЕНИЯ
1. Получить решение разностного уравнения и построить графики · с помощью команд ztrans, i ztrans, ezplot тулбокса SYMBOLIC; · с помощью команд tf и step тулбокса CONTROL; · путем моделирования в SIMULINK; · с помощью команды rsolve пакета MAPLE. 2. Рассчитать абсолютные и относительные численности возрастных групп популяции · с помощью степенной формулы (4); · с помощью команды initial. Построить графики в обычном и логарифмическом масштабах. КОНТРОЛЬНЫЕ ВОПРОСЫ Даны разностные уравнения:
Требуется для уравнения, указанного преподавателем: а) Решить его с помощью характеристического уравнения; б) Решить его при помощи z-преобразования; в) Нарисовать схему моделирования и от нее перейти к матричной форме записи вида (3). 2. Решить двумя способами (по формуле (4) и путем перехода к одному уравнению) систему разностных уравнений
17.Решить систему а) Ответ для А0: Ответдля А1: В пределе для А2: В пределе при больших n
ВАРИАНТЫ ЗАДАНИЙ
1. Варианты коэффициентов a и b разностного уравнения yn +2 + b yn +1+ a yn =1
Литература.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 876; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.249 (0.098 с.) |
 . (1)
. (1) .
.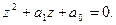
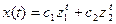 .
.
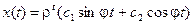 ,
,  .
. . Их положение на комплексной плоскости z = α + i b показано на рис. 1.
. Их положение на комплексной плоскости z = α + i b показано на рис. 1.
 .
.





 , откуда
, откуда  .
.
 :
: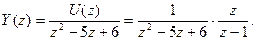
 .
. – вектор переменных, А – квадратная матрица постоянных коэффициентов,
– вектор переменных, А – квадратная матрица постоянных коэффициентов,  .
. ,
,  .
. , X(t)=A t X0=
, X(t)=A t X0= 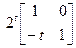

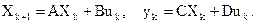 (5)
(5) – вектор состояния; uk, yk – входной и выходной сигналы, A, B, C, D – постоянные матрицы.
– вектор состояния; uk, yk – входной и выходной сигналы, A, B, C, D – постоянные матрицы.

 . Для этого используется та же команда impulse. Реакцию на единичный скачок (переходную функцию) получают при помощи команды step.
. Для этого используется та же команда impulse. Реакцию на единичный скачок (переходную функцию) получают при помощи команды step.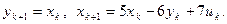
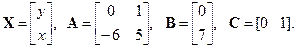
 .
.
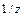 соответственно.
соответственно.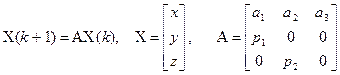 , (6)
, (6) ,
, ,
,

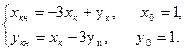

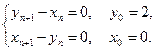
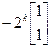

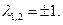
 для трех вариантов матрицы А:
для трех вариантов матрицы А:
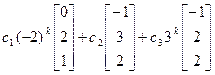
 = y ( n )
= y ( n )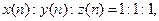 т.к. у матрицы А1 главный собственный вектор [1 1 1]T
т.к. у матрицы А1 главный собственный вектор [1 1 1]T
 .
.


