
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование дифференциальных уравненийСтр 1 из 4Следующая ⇒
МОДЕЛИ ЛИНЕЙНЫХ БЛОКОВ Цель работы:ознакомиться с характеристиками и методикой компьютерного моделирования блоков с дробно-рациональными передаточными функциями с помощью пакетов MATLAB и SIMULINK.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ 1.1. Математическое описание линейных блоков. Рассмотрим линейный блок Q, преобразующий входной сигнал x (t) в выходной сигнал y (t) (рис. 1).
Это означает, что если y 1 и y 2 - реакции блока на входные сигналы x 1 и x 2 , то реакция блока на входной сигнал x = c 1 x 1 + c 2 x 2 должна быть равна y = c 1 y 1 + c 2 y 2 при любых числах c 1, c 2 и любых сигналах x 1, x 2 . Например, линейность интегратора, описываемого уравнением y = a ∫ x d t, следует из известного правила "интеграл суммы равен сумме интегралов":
Для квадратора, описываемого уравнением y = x 2, принцип суперпозиции не выполняется, так как y = (x 1+ x 2)2≠ Удобным средством для моделирования структурных схем в системе MATLAB является SIMULINK. Он содержит библиотеки различных блоков, из которых в рабочем окне с помощью мышки строится структурная схема модели. Рассмотрим некоторые из типовых вычислительных блоков. Масштабный усилитель (обозначается треугольником с надписью gain) реализует математическую зависимость y = ax, где а – коэффициент усиления. Если а = –1 то масштабный усилитель превращается в инвертор – блок, изменяющий знак входного сигнала. Инвертор реализует зависимость у = – х. Сумматор (обозначается кружком, треугольником или прямоугольником с надписью sum) реализует зависимость y = ± x 1 ± x 2 ± x 3, знаки суммирования и число слагаемых можно изменять, щелкнув по блоку мышкой. Оба эти блока находятся в библиотеке (группе блоков) Math Operations. Простейший динамический блок – интегратор (изображается треугольником или прямоугольником с обозначением
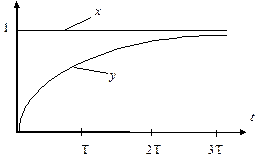
Для установки начального условия у 0 надо войти внутрь блока, щелкнув по нему мышкой. Например, если у 0=2 и на вход интегратора поступает сигнал х= 1, то выходной сигнал определяется формулой y = 2 + t. Это линейно изменяющееся напряжение, осциллограмма которого имеет вид наклонной прямой. Следовательно, прямую наклонную линию можно смоделировать, используя интегратор и масштабный усилитель.
Рис 2 – Получение прямолинейных функций
Соединяя блоки определенным образом между собой, получают схемы для реализации различных функций времени, решения дифференциальных уравнений, моделирования технических объектов. В частности, для получения экспоненциальных функций можно использовать интегратор, охваченный положительной или отрицательной обратной связью (рис. 3, а, б). а) б) в)
    

Чтобы найти вид выходного сигнала первой из этихсхем, выпишем уравнение для ее выходного сигнала
Это дифференциальное уравнение первого порядка относительно переменной y. Решим его методом разделения переменных:
Аналогичные выкладки для второй схемы приводят к выражению y = y 0 e -at. Графикиэтих сигналов показаны на рис. 2, в. В библиотеке Continous имеется также блок для моделирования произвольной передаточной функции (transfer function). Он обозначается прямоугольником с надписью TransferFcn и обозначением
При исследовании и моделировании бортовых систем такими уравнениями пользуются для описания динамики автопилотов, сервоприводов и измерительных датчиков. Постоянные коэффициенты a 0, a 1, b 0, b 1 зависят от технических параметров соответствующих устройств.
Линейному блоку вида (1) соответствует передаточная функция первого порядка. Определение 1. Передаточной функцией Q(p) линейного блока называется отношение изображений по Лапласу его выходного и входного сигналов
при нулевых начальных условиях. Напомним, что изображение по Лапласу F(p) функции f(t) задается формулой
Оно определено для функций f (t), равных нулю при t < 0. Пример 1. Функцией единичного скачка (единичной функцией) называется функция
Ее изображение по Лапласу имеет вид Производная по времени от функции единичного скачка называется дельта-функцией: В пакете MATLAB для получения единичной функции имеется команда stepfun. В SIMULINK эта функция получается с помощью блока step, находящегося в библиотеке Sources (источники). Установим вид передаточной функции блоков первого порядка. Для этого применим к обеим частям уравнения (1) преобразование Лапласа (начальные условия считаем нулевыми)
Отсюда получаем
Здесь X (p) и Y (p) - изображения сигналов x (t) и y (t) по Лапласу, Q (p) – передаточная функция (ПФ) блока Q. Замечание 1. В зарубежной литературе (и в SIMULINK) в качестве аргумента передаточной функции используется буква s. Мы употребляем букву р, придерживаясь традиций отечественной учебной литературы. Замечание 2. В определении ПФ не оговаривается вид входного сигнала. Дело в том, что для линейных блоков отношение Y (p) / X (p) не зависит от вида x (t) (для отношения y (t) / x (t) это, разумеется, неверно). Поэтому при нахождении ПФ можно использовать любой входной сигнал, не равный тождественно нулю. Пример 2. Найдем передаточную функцию интегратора. Полагая x (t)=1(t), получим y (t)= t, t ≥0. Изображения входного и выходного сигналов, соответственно, равны 1/ p и 1/ p 2, следовательно, ПФ интегратора имеет вид Q(p) = 1 / p. Пример 3. Найдем передаточную функцию усилителя с коэффициентом усиления k. Полагая x (t)=1(t), получим y (t)= k · 1(t), т.е. ПФ
1.2. Прохождение сигналов через линейные звенья. Определение ПФ с помощью формулы (2) остается справедливым для линейных стационарных звеньев произвольного порядка, а также для схем, составленных из таких звеньев. Удобство использования передаточной функции состоит в том, что она позволяет определять реакцию y (t) звена Q на любой конкретный входной сигнал x (t). Для этого находят изображение X (p) входного сигнала (по таблице преобразований Лапласа) и умножают его на передаточную функцию Q (p), получая тем самым изображение выходного сигнала Y (p). Затем, используя таблицу, выполняют обратный переход от найденного изображения к оригиналу y (t). Пример4. Найдем реакцию сервопривода с передаточной функцией Q (p) = k / (T p+ 1)(апериодическое звено) на управляющее воздействие x (t) = 1 (t). Коэффициент усиления сервопривода k =1, постоянная времени T = 0,1 c.
В соответствии с примером 1
Обращаясь к таблице преобразований Лапласа, находим соответствующий оригинал
Пример 5. Найдем реакцию изодромного звена с передаточной функцией Изображение входного сигнала имеет вид
Выполняем разложение на простейшие дроби (используя метод неопределенных коэффициентов)
Постоянные A, B, C находим, приводя выражение в правой части к общему знаменателю.
Затем приравниваем коэффициенты при одинаковых степенях p в числителях правой и левой части получаем систему трех алгебраических уравнений с тремя неизвестными А+В=2; В+С=0; А+С=0. Решая систему получим: A = B = 1; С = – 1. Тогда Возвращаясь к оригиналам (см. таблицу преобразований Лапласа в приложении), получаем y (t)= e - t + cos t -sin t. Ввиду того, что реакция звена на импульсное или ступенчатое воздействие исчерпывающим образом характеризует линейное звено, в теории управления для них используются специальные термины. Определение 2. Импульсной весовой характеристикой (весовой функцией) q (t) называется реакция звена на входной сигнал x (t) = d(t). Импульсной переходной характеристикой (переходной функцией) p (t) называется реакция звена на входной сигнал x (t) = 1 (t). Эти функции связаны соотношением
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА В первой части лабораторной работы исследуются схемы моделирования, показанные на рис. 4, а, б, в. Числовые значения параметра k приведены в таблице вариантов, начальные условия и значение с рассчитываются по формулам Начальные условия в интергаторы записываются в поле: Initial condition (на рис. 5 - начальные условия обозначены цифрами со стрелкой вниз). Отчет по первой части работы должен содержать: I. Схемы рис. 5 с заданными численными значениями y 0, k, c, нарисованные применительно к SIMULINK (с указанием блока входного сигнала и осциллографов).
а) б) в)
Рис. 5. Исследуемые схемы моделирования
2. Вывод формул для выходных сигналов каждой из схем. Таблицы и графики этих сигналов, координаты точки экстремума функции z (t) и тангенс угла ее наклона в начале координат. Во второй части лабораторной работы исследуется линейное звено первого порядка, которое описывается дифференциальным уравнением а) x (t) = 1 (t), б) x (t) = e – t, в) x (t) = sin t, г) x (t) = d(t). Отчет по второй части должен содержать: 1. Дифференциальное уравнение и передаточную функцию заданного блока. 2. Вывод формул y (t) для всех вариантов входного сигнала (см. пример 5). 3. Таблицы и графики теоретических значений y (t) для всех случаев. Графики выходных сигналов в пакете MATLAB можно получить путем ввода в рабочем окне (Command Window) следующих выражений: 1) Задаем интервал времени моделирования: t=0:0.01:20; 2) Вводим формулу или выражение: y=exp(-t)+cos(t)-sin(-t); 3) Строим график функции: plot(t,y); grid. 4. Схемы моделирования в пакете SIMULINK.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Первая часть. 1. С помощью пакета SIMULINK собрать схему рис. 5, а, установить коэффициенты усиления и начальные условия. Наблюдать выходные сигналы схемы с помощью осциллографа Scope. Зарегистрировать с помощью осциллографа момент пересечения графиков x (t) и y (t), сравнить его с теоретическим. 2. Собрать схему рис. 5, б. Для этого в предыдущей схеме (а) отключить входной сигнал и охватить каждый интегратор обратной связью. Наблюдать выходные сигналы интеграторов с помощью осциллографа, сравнить их с теоретическими. 3. Собрать схему рис. 5, в. Для этого взять сумматор, и усилитель с коэффициентом с и соединить их входы с выходами интеграторов из предыдущей схемы (б). Наблюдать осциллограмму сигнала z (t), сравнить теоретические и экспериментальные координаты точки экстремума. Вторая часть. 1. Построить схему моделирования, содержащую генератор входного сигнала и блок с заданной передаточной функцией. 2. Выбрать параметры (численный метод, время моделирования) и выполнить моделирование. Наблюдать результат моделирования в виде графика. 3. Получить переходные функции звеньев второго порядка с передаточными функциями 1/(p 2 + b), p /(p 2 + b), 1/(p 2 + ap + b), 1/(p 2 – ap + b). 4. Выполнить те же пункты в пакете MATLAB, используя команды step, impulse, lsim, plot.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие блоки, объекты и системы называются линейными? Являются ли линейными следующие блоки: усилитель; интегратор; апериодическое звено; усилитель, включенный последовательно с диодом; пассивная интегрирующая RC-цепочка? 2. Имеется интегратор нулевыми начальными условиями. Нарисовать вид выходного сигнала, если на вход интегратора подаются:
а) х = 1 (t), б) x = sin t, в) x = соs t, г) x = et, д) x = е– t е) х = t, ж) х = t 2. 3. Выполнить задание п. 2 для случая двух одинаковых последовательно включенных интеграторов. 4. Как подать выходной сигнал интегратора на вход осциллографа? Как изменить длительность развертки осциллографа? Как наблюдать одновременно два сигнала? 5. Найти передаточную функцию усилителя, интегратора, апериодического звена, двух последовательно соединенных интеграторов. Написать соответствующие дифференциальные уравнения. 6. Найти передаточную функцию интегратора, полагая x (t) = et, e – t, sin t, t. 7. Выполняя интегрирование, найти изображения по Лапласу сигналов et, e – t, e – t + e t, 1 – e – t. 8. Найти реакцию апериодического звена на сигналы из п. 7 и нарисовать соответствующие графики. 5. ВАРИАНТЫ ЗАДАНИЙ
Практическая работа № 2
АНАЛИЗ СИСТЕМЫ УПРАВЛЕНИЯ
Цель работы: исследовать теоретически и с помощью пакета MATLAB устойчивость, управляемость, наблюдаемость и минимальность системы управления, заданной структурной схемой, и построить ее модель пониженного порядка.
1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.1 Анализ устойчивости. Понятие устойчивости является одним из основных в теории управления. Устойчивой называют систему, которая, будучи выведена из состояния равновесия, стремится вновь вернуться в это состояние. Для неустойчивых систем характерна обратная тенденция. Примером неустойчивой системы может быть карандаш, стоящий на острие. Обычно исследование устойчивости систем сводится к анализу устойчивости соответствующих дифференциальных уравнений. У неустойчивых уравнений решение неограниченно возрастает со временем. В теории автоматического управления существуют различные методы анализа устойчивости. Для линейных систем разработаны критерии устойчивости, которые можно разделить на корневые, алгебраические и частотные. Корневойкритерий устойчивости. Для того чтобы линейная динамическая система была устойчивой, необходимо и достаточно, чтобы все корни ее характеристического уравнения лежали в левой комплексной полуплоскости. Например, математическая модель системы, описываемой дифференциальным уравнением
устойчива, так как корни характеристического уравнения р 2+2 р +5=0 имеют отрицательные вещественные части p 1,2= –1±2 i, т.е. лежат слева от оси ординат. Алгебраический критерий устойчивости. Алгебраические критерии устойчивости позволяют судить об устойчивости на основе анализа коэффициентов характеристического полинома. Наибольшую известность получил критерий устойчивости Гурвица. Из него, в частности, следует, что все коэффициенты устойчивого дифференциального уравнения должны быть положительны. Для уравнений второго порядка это необходимое и достаточное условие. Для уравнений третьего порядка
помимо положительности коэффициентов, должно выполняться дополнительное условие, а именно, произведение средних коэффициентов должно быть больше произведения крайних: а 2 а 1> а 0 а 3. Например, уравнение Частотный критерий устойчивости. Частотные критерии носят графический характер. Они опираются на анализ графиков частотных характеристик – АЧХ, ФЧХ, АФХ (последняя известна также как диаграмма Найквиста). Часть из них позволяет делать заключение об устойчивости замкнутой системы управления по частотным характеристикам разомкнутой системы. Приведем в качестве примера критерий Найквиста. Обозначим передаточную функцию разомкнутой системы Q(p) и охватим ее единичной отрицательной обратной связью (рис. 1).
Пусть известно, что разомкнутая система устойчива. Тогда для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста разомкнутой системы не охватывал точку с координатами (-1, 0 j) на комплексной плоскости. В тулбоксе CONTROL пакета MATLAB диаграмма Найквиста системы sys строится командой nyquist(sys), указанная точка помечена на ней красным крестиком. В лабораторной работе исследуется система управления, заданная структурной схемой, поэтому для анализа устойчивости надо сначала найти ее передаточную функцию. Структурная схема исследуемой системы приведена на рис. 2. В ее состав входят три апериодических звена, а также суммирующие и вычитающие звенья. В схеме можно указать три пути от входа до выхода с передаточными функциями
Рис. 2. Структура исследуемой системы
Общая передаточная функция получается, как их сумма
Здесь A(p) и B(p) – некоторые полиномы от p (свои для каждого варианта). Характеристический полином системы равен знаменателю этой передаточной функции
На основе приведенных выше критериев устойчивости можно заключить, что если коэффициенты T 1, T 2, T 3 положительны, то система будет устойчивой. Анализ устойчивости замкнутой системы можно осуществить с помощью критерия Найквиста.
1.2. Анализ управляемости и наблюдаемости. Понятия управляемости и наблюдаемости широко используются в современной теории автоматического управления. Линейная система называется управляемой, если с помощью входного сигнала ее можно перевести из начала координат в любую точку пространства состояний. Система называется наблюдаемой, если по измерениям входного и выходного сигналов можно однозначно определить ее начальное состояние. Анализ управляемости и наблюдаемости выполняется с помощью матриц управляемости и наблюдаемости или с помощью грамианов управляемости и наблюдаемости. Те и другие строятся по описанию в пространстве состояний
Чтобы получить такое описание, воспользуемся структурной схемой, приведенной на рис. 2. Выпишем операторные уравнения для каждого блока схемы
и преобразуем их к виду
Выполняя обратное преобразование Лапласа, получаем систему линейных дифференциальных уравнений первого порядка
Кроме того, имеем алгебраическое уравнение для выходного сигнала y= x 1– x 3. Переписывая эти уравнения в матричной форме (3), получаем следующие выражения для матриц A, b, c:
где ненулевые элементы матриц имеют вид
Теперь можно перейти к анализу управляемости и наблюдаемости. Сформируем на основе матриц A, b, c две вспомогательные матрицы
Матрицы R и D называются соответственно матрицей управляемости и матрицей наблюдаемости системы. В пакете MATLAB их можно построить с помощью команд ctrb и obsv. К ритерийуправляемости. Для того чтобы система (3) была управляемой, необходимо и достаточно, чтобы матрица управляемости имела полный ранг rankR = n. К ритерийнаблюдаемости. Для того чтобы система (3) была наблюдаемой, необходимо и достаточно, чтобы матрица наблюдаемости имела полный ранг rankD = n. В случае систем с одним входом и одним выходом матрицы R и D квадратные, поэтому для проверки управляемости и наблюдаемости достаточно вычислить определители матриц R и D. Если они не равны нулю, то матрицы имеют полный ранг. Другой способ проверки управляемости и наблюдаемости опирается на вычисление грамианов управляемости и наблюдаемости. Так называются симметричные квадратные матрицы Wc и Wo, определяемые равенствами
В пакете MATLAB их можно найти с помощью команд типа gram(sys, ‘c’), gram(sys, ‘o’). Необходимые и достаточные условия управляемости и наблюдаемости имеют вид det Wc¹0, det Wo¹0.
1.3 Анализ минимальности моделей. Одной и той же передаточной функции Q (p) можно сопоставить целый класс эквивалентных реализаций в пространстве состояний, характеризуемых различными тройками матриц (A, b, c) разных, вообще говоря, размеров. Реализация называется минимальной, если размер ее матрицы A наименьший среди всех эквивалентных реализаций. Поиск такой реализации имеет практический смысл, так как ее моделирование на ЭВМ требует меньших вычислительных затрат. Для анализа минимальности реализации нужно проверить ее управляемость и наблюдаемость. К ритерийминимальности. Для того чтобы реализация (3) была минимальной, необходимо и достаточно, чтобы она была управляемой и наблюдаемой одновременно. Таким образом, анализ минимальности конкретной реализации сводится к проверке пары критериев rankR= n, rankD= n. Если хотя бы один из рангов меньше n, то реализация неминимальна. Размерность эквивалентной минимальной реализации n0 определяется по формуле n 0= rank(RD). Анализ минимальности с помощью грамианов управляемости и наблюдаемости проводится аналогично. Критерием минимальности служит выполнение условия det(WcWo)¹0, эквивалентного паре условий det Wc¹0, det Wo¹0. Если исходное описание реализации оказалось неминимальным, то возникает задача перехода к минимальной реализации. Чтобы решить ее, сначала перейдем от описания в пространстве состояний (3) к передаточной функции
Далее нужно выделить общий множитель в числителе и знаменателе передаточной функции Q (p) и сократить на него. Эта процедура известна, как сокращение совпадающих нулей и полюсов системы. Отметим ряд соотношений между элементами матриц А, b, c и коэффициентами передаточной функции, вытекающих из формулы (4),. Знаменатель передаточной функции совпадает с характеристическим полиномом матрицы А
А(p)=det(p E-A) = pn + an - 1 pn -1 +...+ a 1 p + a 0.
Его корни l 1,..., l n равны собственным числам матрицы А, а коэффициенты а 0 и an- 1 с точностью до знака равны ее определителю и следу
Старший и младший коэффициенты числителя передаточной функции
В(p)= bn - 1 pn -1 +...+ b 1 p + b 0 удовлетворяют соотношениям bn -1 = cb, b 0/ a 0= - c A-1 b. (6)
Величина k 0= b 0/ a 0 называется статическим коэффициентом усиления. Она равна установившемуся значению переходной функции системы. В пакете MATLAB для вычисления статического коэффициента усиления имеется команда dcgain (от direct current gain – коэффициент усиления по постоянному току). В ее основу положена формула k 0=Q(0). Приведенные соотношения удобно использовать для контроля вычислений. Получение минимальной реализации в пакете MATLAB осуществляется командой minreal, для вычисления нулей и полюсов можно использовать функции zero, pole, pzmap, zpk. Аргументом во всех случаях служит исследуемая система sys, предварительно сформированная командами ss или tf.
2. ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА
1. Нарисовать схему рис.2 для своего варианта и найти ее передаточную функцию по формуле (1). 2. Проверить устойчивость системы, используя алгебраический и корневой критерии. 3. Получить для своего варианта схемы описание в пространстве состояний вида (3) и выписать матрицы A, В, С. 4. Найти матрицы управляемости и наблюдаемости системы, определить их ранги и сделать вывод об управляемости, наблюдаемости и минимальности системы. 5. Найти передаточную функцию по формуле (4), и сравнить ее с полученной в п.1. Проверить выполнение соотношений (5), (6). Тремя способами (по структурной схеме, передаточной функции и описанию в пространстве состояний) найти статический коэффициент усиления системы. 6. Определить порядок минимальной реализации и найти ее передаточную функцию, выполнив сокращение нулей и полюсов. Найти реакцию минимальной реализации на единичный скачок и построить ее график. 7. Привести программы на языке MATLAB для выполнения пунктов 2 – 6 и краткое описание назначения и синтаксиса команд rank, ss, tf, zpk, zero, pole, pzmap, ctrb, obsv, minreal, dcgain.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. В диалоговом режиме пакета MATLAB ввести матрицы A, b, c и сформировать ss-описание системы sys=ss(A, b, c, 0). Используя команды pole, eig, pzmap, найти полюсы системы и получить график их расположения на комплексной плоскости. Сделать вывод об устойчивости. Построить диаграмму Найквиста системы и сделать заключение об устойчивости системы, охваченной обратной связью (рис.1). 2. Найти матрицы управляемости и наблюдаемости, вычислить их определители и ранги. Сделать вывод об управляемости, наблюдаемости и минимальности. Найти грамианы управляемости и наблюдаемости. 3. С помощью команд tf и zpk перейти к передаточной функции. Двумя способами получить минимальную реализацию (сокращая нули и полюса, и с помощью команды minreal). Сравнить переходные функции исходной и минимальной реализаций, а также их статический коэффициент усиления. 4. Набрать схемы исходной и минимальной реализаций в SIMULINK и сравнить их реакции на одинаковые входные сигналы.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Найти передаточные функции систем, заданных в пространстве состояний тройкой матриц:
2. Найти ранги матриц управляемости и наблюдаемости для систем из п.1. 3. Нарисовать структурные схемы систем, матрицы которых приведены ниже.
Определить, какие из них являются: а) устойчивыми; б) управляемыми; в) наблюдаемыми; г) минимальными. 4. Система управления задана структурной схемой, показанной на рис. 3.
Требуется: а) найти статический коэффициент усиления схемы;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-11-02; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.248.47 (0.209 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Напомним, что блок называется линейным, если он удовлетворяет принципу суперпозиции, который нестрого формулируется следующим образом: следствие от суммы причин равно сумме следствий от каждой из причин, взятых в отдельности.
Напомним, что блок называется линейным, если он удовлетворяет принципу суперпозиции, который нестрого формулируется следующим образом: следствие от суммы причин равно сумме следствий от каждой из причин, взятых в отдельности. .
. , поэтому квадратор является нелинейным блоком.
, поэтому квадратор является нелинейным блоком. внутри и надписью integrator). Он находится в библиотеке Continuos и реализует зависимость
внутри и надписью integrator). Он находится в библиотеке Continuos и реализует зависимость
 На рисунке 2а приведен пример моделирования уравнения прямой y = k×x + b. На выходе интегратора мы получаем линейно изменяющийся выходной сигнал, имеющий вид наклонной прямой (см. рис. 2б)
На рисунке 2а приведен пример моделирования уравнения прямой y = k×x + b. На выходе интегратора мы получаем линейно изменяющийся выходной сигнал, имеющий вид наклонной прямой (см. рис. 2б)








 Рис. 3. Получение экспоненциальных функций
Рис. 3. Получение экспоненциальных функций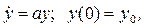 где
где 

 внутри. Он, в частности, позволяет моделировать линейные блоки, которые можно описать дифференциальным уравнением первого порядка
внутри. Он, в частности, позволяет моделировать линейные блоки, которые можно описать дифференциальным уравнением первого порядка . (1)
. (1) (2)
(2) . (3)
. (3)
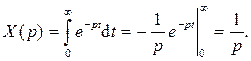
 . Она равна нулю везде, кроме точки t = 0, в которой она принимает бесконечно большое значение. Ее инженерная интерпретация – очень короткий импульс единичной площади. Операции дифференцирования по времени соответствует умножение на оператор р в области изображений по Лапласу, поэтому для изображения функции d (t) получаем
. Она равна нулю везде, кроме точки t = 0, в которой она принимает бесконечно большое значение. Ее инженерная интерпретация – очень короткий импульс единичной площади. Операции дифференцирования по времени соответствует умножение на оператор р в области изображений по Лапласу, поэтому для изображения функции d (t) получаем  .
. .
. .
. .
. , следовательно,
, следовательно,  . Представим Y (p) в виде суммы простейших дробей
. Представим Y (p) в виде суммы простейших дробей .
.
 , на входной сигнал X = cos(ω t), если k = 2, T = 1 c,
, на входной сигнал X = cos(ω t), если k = 2, T = 1 c,  , поэтому
, поэтому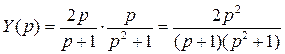 .
. .
.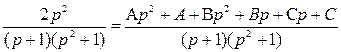

 , которое следует из равенства
, которое следует из равенства  . Отсюда вытекает, что при компьютерном моделировании весовую характеристику блока с ПФ Q(p), т.е. реакцию на x (t)=d(t), можно получить, подавая единичный скачок на блок с ПФ p Q (p). Другой способ – использовать сигнал с входа выходного интегратора схемы.
. Отсюда вытекает, что при компьютерном моделировании весовую характеристику блока с ПФ Q(p), т.е. реакцию на x (t)=d(t), можно получить, подавая единичный скачок на блок с ПФ p Q (p). Другой способ – использовать сигнал с входа выходного интегратора схемы.

 Параметры k, b, берутся из таблицы вариантов. В отчете требуется для заданных значений k и b найти теоретически выходной сигнал блока y (t), если входной сигнал имеет вид:
Параметры k, b, берутся из таблицы вариантов. В отчете требуется для заданных значений k и b найти теоретически выходной сигнал блока y (t), если входной сигнал имеет вид: 
 ,
, неустойчиво, так как 2×0,5<1×3.
неустойчиво, так как 2×0,5<1×3.


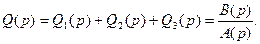 (1)
(1) (2)
(2) (3)
(3)




 ,
, 
 .
. (4)
(4)




