
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знаки и индексы, нанесенные на линейке
π = 3,14 —отношение длины окружности к диаметру; нанесен на шкале 1 и может использоваться для решения задач, связанных с определением длины окружности;
t 360 —нанесен на шкале 1, служит для определения времени разворота самолета на 360°;
® —нанесен красной краской на шкале 4 и служит для решения задач по определению радиуса разворота самолета;
Для решения задач несколько шкал линейки НЛ-10м, как правило, используются одновременно. Шкалы, при помощи которых производят решение задач по определенным формулам, называются смежными. Обычно они построены по одному закону и в одном масштабе.
Рассмотрим последовательно назначение и построение всех смежных шкал линейки НЛ-10м. Шкалы 1 — расстояние (км) — скорость км/час, 2 — время (в мин. или сек.) —время (в час. или мин.) в основном служат для решения формулы S = Wt, (1) где S — расстояние в км (м); W — путевая скорость в км/час (м/сек); t — время полета в час., мин. или сек.
На корпусе линейки на неподвижной шкале 1 в определенном масштабе нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000, имеющих размерность расстояния в м или км и скорости в км/час или м/сек. Эти значения в 10,100 и т. д. раз можно увеличивать или уменьшать.
На нижней подвижной шкале 2 (на движке линейки) в том же масштабе нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000, но оцифрованные в единицах времени от 1 минуты до 16,6 часа или от 1 секунды до 16,6 минуты. В середине шкалы имеется выделенный индексами На рис. 4 показана схема решения задач по этим шкалам. Значение путевой скорости W км/час устанавливается и отсчитывается по шкале 1 против индекса Шкалы 3 — синусы, 4 — тангенсы и 5 — радиусы разворота — расстояния — высоты предназначены для решения формул S = Н tg α — на шкалах 4 и 5 (3) и S 1 = H sin α. — на шкалах 3 и 5, (4) где S и S 1 — расстояние в м или км Н — высота в м или км; α — угол в град. На неподвижной шкале 5 на корпусе линейки нанесены деления, соответствующие значению логарифмов чисел от 1 до 1000 (шкала 5 одинакова со шкалой 1), которые можно принимать за расстояния, высоты и радиусы разворота самолета в м или км. На движке нанесены логарифмы значений тангенсов углов от 0,5 до 85° (шкала 4) и логарифмы значений синусов углов от 5 до 90° или от 175 до 90° (шкала 3). Шкала 6 является дополнительной и может использоваться совместно со шкалами 1, 2, 3, 4 и 5. Она построена в 2 раза крупнее по масштабу, т, е имеет модуль М= 168 мм и ее деления соответствуют значениям логарифмов чисел от Шкалы 7 — сумма температур (t0 + tH), 8 — исправленная высота, 9 — высота по прибору и индекс
На верхней неподвижной шкале 7 нанесены логарифмы чисел, соответствующие сумме температур на земле и высоте полета (t0 + tH) в диапазоне от + 90 до—120°, это исключает ненужную операцию по определению средней температуры.
На шкале 8 на корпусе линейки нанесены логарифмы чисел, соответствующие исправленному значению высоты полета в диапазоне от 400 до 12000 м. На подвижной шкале 9 (на движке) нанесены логарифмы величины ω, соответствующие значению высоты полета по прибору от 400 до 12000 м.
Шкалы 10 — температура для высоты более 11 000 м, 14 — исправленная высота и скорость, 15 — высота и скорость по прибору и индекс На верхней подвижной шкале 10 нанесены логарифмы чисел, соответствующие температуре на высоте полета в диапазоне от —30 до —75°С, и на шкале 14 (верхняя оцифровка шкалы) — логарифмы чисел, соответствующие исправленному значению высоты в диапазоне от 12 до 25 км. На нижней неподвижной шкале 15 нанесены логарифмы чисел, соответствующие значению высоты по прибору от 12 до 23 км (нижняя оцифровка). Установочный индекс Введение данной поправки вызвано тем, что фактическая высота слоя тропопаузы (т. е. высоты, с которой начинается постоянство температуры) для средних широт равна 9000—13 000 м и отличается от стандартной, которая принята для построения шкалы высотомера постоянной и равна 11 000 м.
Шкалы 11 — температура на высоте для скорости, 12 — высоты по прибору (км), 14 — исправленные высота и скорость, 15 — высота и скорость по прибору служат для пересчета показаний аэродинамических указателей скорости (типа УС-700.или УС-800), построенных на принципе измерения скоростного напора встречного потока воздуха, в исправленную скорость с учетом методической ошибки прибора из-за несоответствия фактической плотности воздуха на высоте расчетной плотности, по которой построена шкала прибора.
Шкалы 11 и 12 являются установочными, а шкалы 14 и 15 — основными, служащими для снятия отсчетов определяемых величин. На шкале 11 (на движке) нанесены логарифмы величины τ, соответствующие значениям температуры воздуха на высоте от + 30 до — 70°С. На шкале 12 (неподвижная шкала на корпусе линейки) нанесены логарифмы величины Н, соответствующие высоте по прибору от 0 до 12 км, На шкале 14 нанесены логарифмы чисел, соответствующие исправленному значению скорости от 100 до 1400 км/час, а на шкале 15 — логарифмы чисел, соответствующие значению скорости по прибору от 100 до 1200 км/час. Пересчет скорости по этим шкалам выполняется без учета сжимаемости воздуха.
На рис. 8 показана схема решения задачи пересчета скорости по шкалам 11, 12, 14 и 15. Шкала 13 — высоты по прибору (км) для КУС совместно со шкалами 11, 14 и 15 служит для пересчета показаний комбинированных указателей скорости (КУС) в исправленную скорость с учетом поправки на температуру из-за несоответствия фактического распределения температуры воздуха по высотам стандартным условиям распределения температуры, по которым построена шкала прибора. В КУС, в отличие от обычных указателей скорости, с помощью анероидной коробки сообщается дополнительный поворот второй (тонкой) стрелке указателя скорости с поднятием на высоту. Этим вводится поправка на изменение плотности воздуха с высотой и поправка на сжимаемость с учетом плотности воздуха.
Шкала 16 служит для определения ошибок термометра наружного воздуха в полете вследствие нагревания его чувствительного элемента в заторможенном потоке или наличия трения о воздух. Величина поправки Δt зависит от истинной скорости полета и выражается формулой:
где V — истинная воздушная скорость в км/час; 0,265 — коэффициент пропорциональности. По этой зависимости и построена шкала 16 (см. рис. 3). При всех пересчетах высоты и скорости необходимо по этой шкале найти поправку Δ t и исправить показания термометров (типа ТУЭ или спиртового) по формуле, помещенной справа от шкалы:
Для термометров, замеряющих температуру воздуха при полном торможении, поправка выражается формулой
ИЛИ
таккак коэффициент 0,385 больше 0,265 приблизительно в 1,5 раза.
Умножение и деление чисел.
Для умножения и деления чисел используются шкалы 1 и 2 или 5 и 2, а также шкалы 14 и 15. Шкалы 1, 2 и 5 используются для умножения и деления в основном при решении специальных задач, связанных с расчетом скорости, высоты, времени полета и других навигационных элементов. Шкалы 14 и 15 имеют деления с большим масштабом, и потому на них умножение и деление чисел можно выполнять с большей точностью (с большим числом значащих цифр). При всех вычислениях на логарифмических шкалах необходимо знать и соблюдать следующие правила:
1. При отсчетах или установках по шкалам искомые или заданные числа можно увеличивать или уменьшать в 10,100 и т. д. раз. 2. В искомом результате важно правильно отделить число знаков (число цифр) слева от запятой. У десятичной дроби число знаков считается отрицательным и равным числу нулей справа от запятой до первой значащей цифры. 3. Число знаков произведения равно алгебраической сумме числа знаков множимого и множителя, если против множимого устанавливалось деление 4. Число знаков частного равно алгебраической разности числа знаков делимого и делителя, если отсчет частного был сделан против деления
Подсчет и определение количества знаков при умножении и делении занимает некоторое время и требует запоминания правил. Чтобы избежать ошибок в определении количества знаков результата вычисления на линейке нужно грубо определить ответ в уме. Зная возможный порядок вычисляемых величин, можно всегда судить о количестве знаков результата, учитывая при этом размерность входных и исходных величин.
Порядок умножения (шкалы 14 и 15): — передвигая движок, установить деление 100 или
— установить визирку по шкале 14 на деление, соответствующее множителю; — отсчитать по визирке на шкале 15 искомое произведение. Примеры: 1) 16,4 х 19,2 = 315. Число знаков множимого 2, множителя 2, произведения (2+2) — 1 =3 (рис. 10, а). 2) 8,43 х 6,65 = 56. Число знаков множимого 1, множителя 1, произведения (1 + 1)=2 (рис. 10, б). 3) 0,0065 х 3550 = 23,2. Число знаков множимого —2, множителя +4, произведения (— 2 +4) = 2. 4) 0,125 х 0,214 = 0,0268. Число знаков множимого 0, множителя 0, произведения (0+0) — 1= —1.
Порядок деления (шкалы 14 и 15): — установить визирку по шкале 15 на деление, соответствующее делимому
— передвигая движок, подвести под визирку деление шкалы 14, соответствующее делителю; — отсчитать по шкале 15 против деления 100 или
Примеры. 1) 181: 15,2 = 11,9. Число знаков делимого 3, делителя 2, частного (3—2) + 1 = 2. 2) 67,5: 73 = 0,926. Число знаков делимого 2, делителя 2, частного (2—2) = 0. 3) 0,0225: 0,0172 = 1,31. Число знаков делимого —1, делителя —1, частного (-1)-(-1) +1 = 1. 4) 678: 0,73 = 927. Число знаков делимого 3, делителя 0, частного (3+0) = 3.
Примечание. Порядок умножения и деления чисел на шкалах 1 и 2 отличается лишь тем, что вместо деления 100 и индекса
ИЗВЛЕЧЕНИЕ КВАДРАТНЫХ КОРНЕЙ ИЗ ЧИСЕЛ И ВОЗВЕДЕНИЕ ИХ В КВАДРАТ. Порядок решения (шкалы 5 и 6):
— установить визирку по шкале 6 на деление, соответствующее основанию степени, или по шкале 5 — на деление, соответствующее степени числа (рис. 12);
— отсчитать по визирке на шкале 5 искомое значение степени (квадрата числа) или по шкале 6 значение основания (корня квадратного из числа).
Примечания: 1. Число знаков квадрата числа равно удвоенному числу знаков основания, если квадрат числа отсчитывается на среднем интервале шкалы 5 (от 10 до 100); или на единицу меньше удвоенного, если отсчитывается на правом или левом интервалах (от 1 до 10 или от 100 до 1000).
2. Число знаков квадратного корня равно числу граней (включая и неполные), если подкоренное число больше или равно 1, или числу чисто нулевых граней, взятому со знаком минус, если подкоренное число меньше единицы; при этом «нуль целых» за грань не считается. 3. Квадратные корни с четным количеством знаков подкоренного выражения извлекаются по среднему интервалу шкалы 5 (10—100), с нечетным количеством знаков— по правому или левому интервалам шкалы 5 (100—1000 или 1—10). 4. Число, возводимое в квадрат, и значение подкоренного выражения можно увеличивать или уменьшать в 10, 100 и т. д. раз и соответственно в 102, 1002 и т. д. раз увеличивать или уменьшать результат. Примеры: 1) 9,8122 = 96,3. Число знаков результата (1 х 2) = 2. 2) 2,3522 = 5,52. Число знаков результата (1 х 2) —1 = 1. 3) 17,622=309. Число знаков результата (2 х 2) —1 = 3. 4). Число граней 1, число знаков результата 1. 5). Число граней (неполных) 2, число знаков результата 2. 6). Число граней (нулевых) 1, число знаков результата —1. ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Определение значений синуса и тангенса заданного угла а (рис. 14) производится по формулам
Порядок решения (шкалы 3, 4 и 5): — передвигая движок, установить индекс — установить визирку по шкале 4 на деление, соответствующее заданному углу, если находится тангенс и синус угла (угол меньше 5° или больше 175°), или по шкале 3, если находится синус угла (угол больше 5° или меньше 175°);
— отсчитать по визирке на шкале 5 (или 1) искомое значение синуса или тангенса угла, число значащих цифр зависит от цены деления данного участка шкалы и определяется интерполяцией последнего деления «на глаз».
Примечание. Для определения значений косинусов и котангенсов углов необходимо визирку устанавливать по шкале 3 или 4 на значения дополнений углов до 90°, т. е. на значения (90°—α), где α — заданный угол.
Примеры: 1) sin45° = 0,70. 2) sinl5° = 0,26. 3) sinl73° = 0, 122. 4) tg56°=l,48. 5) tg25° = 0,467. 6) cos70° = sin20° = 0,341. 7) ctg21° = tg69° = 2,6.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ЧИСЛА НА ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛОВ а) Умножение числа на синус и косинус угла: a = b·sin a; d = b·cos a.
Порядок решения (шкалы 3 и 5): — передвигая движок, установить индекс угла против деления шкалы 5, соответствующего числу (рис. 16 и 17); — установить визирку по шкале 4 (если заданный угол меньше 5° или больше 175°) или по шкале 3 (если заданный угол больше 5° или меньше 175°) на деление, соответствующее заданному углу; — отсчитать по визирке на шкале 5 искомое произведение.
Примечание. Для умножения числа на значение косинуса угла необходимо устанавливать визирку на деление шкалы 3 или 4, соответствующее дополнению угла до 90°, т. е. (90° — α). Пример. Дано: b = 325; а = 28°. Определить: α = 325 sin 28° = 152; d = 325 cos 28° = 325 sin 62° = 286. б) Умножение числа на тангенс и котангенс угла α = b tg α; d = b·ctg α. Порядок решения (шкалы 4 и 5): — передвигая движок, установить индекс
— установить визирку по шкале 4 на деление, соответствующее заданному углу; — отсчитать по визирке на шкале 5 искомое произведение. Примечание. Для умножения чисел на котангенс угла необходимо устанавливать визирку по шкале 4 на деление, соответствующее дополнению угла до 90°, т. е. (90° — α).
Пример. Дано: b = 15,4; а = 58°. Определить: а = 15,4 tg 58° = 24,6; d = 15,4 ctg 58° = 15,4 tg 32° = 9,62.
в) Деление числа на синус и тангенс угла
Порядок решения (шкалы 3 и 5): — установить визирку по шкале 5 на деление, соответствующее заданному числу (рис. 18 и 19);
— передвигая движок, подвести под визирку деление шкалы 4 (если число делится на тангенс или заданный угол меньше 5° или больше 175°) или шкалы 3 (если число делится на синус и заданный угол больше 5° или меньше 175°), соответствующее заданному углу; — отсчитать по шкале 5 против индекса
Примечания: 1. При делении чисел на косинус угла необходимо подводить под визирку деления шкалы 3 или 4, соответствующие дополнению угла до 90°, т. е. (90° — α). Пример. Дано: b = 123; а = 36°. Определить: 2. Величины тангенса и котангенса угла являются взаимообратными. Поэтому деление на эти величины целесообразно заменить умножением, а именно:
Порядок решения таких выражений описан выше. Примеры: 1) 2) 3. При умножении или делении чисел на значения секансов или косекансов углов целесообразно заменить умножение чисел на значения секансов или косекансов углов делением чисел на значения косинусов или синусов этих углов, а деление заменить умножением и выполнять указанные действия так же, как описано выше. Примеры: 1) 2) 3) 4)
КОМБИНИРОВАННЫЕ ДЕЙСТВИЯ. К комбинированным действиям относится решение задач, в которых имеются различные действия: умножение и деление чисел на значения тригонометрических функций, на значения корней квадратных из чисел или значения квадратов чисел и т. п. При решении таких задач на линейке необходимо чередовать действия умножения и деления, чтобы не получать больших или малых величин, выходящих за пределы шкал. Порядок решения задач, в которых используются комбинированные действия, рассмотрены ниже. Для примера показано решение задачи по вычислению радиуса круга вероятных местонахождений самолета при определении места самолета при помощи угломерных радиотехнических систем. Задача решается по формуле:
где r — радиус круга вероятного местонахождения самолета; S1 — расстояние до первой пеленгуемой радиостанции в км$ S 2 — расстояние до второй пеленгуемой радиостанции в км; ψ— угол станций; Δ П —ошибка в пеленге в град. Порядок решения (шкалы 1, 2, 3, 5 и 6): — вычислить величину
— передвигая движок, установить индекс — установить визирку по шкале 2 на деление, соответствующее величине — передвигая движок, подвести под визирку деление шкалы 3, соответствующее значению угла ψ, и перевести визирку по шкале 2 на деление, соответствующее значению ΔП; — отсчитать по визирке на шкале 1 (или 5) искомое значение r. Пример. Дано: S1 = 135 км; S2 = 95 км; ΔП = 3°; ψ = 130°. Находим:
|
||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.230.44 (0.151 с.) |
 — нанесен краcной краской на шкале 2, служит для перевода скоростей, выраженных в км/час, в м/сек и обратно, соответствует делению 36;
— нанесен краcной краской на шкале 2, служит для перевода скоростей, выраженных в км/час, в м/сек и обратно, соответствует делению 36; —нанесен красной краской на шкале 2, служит для решения задач, связанных с определением времени полета, пройденного расстояния и путевой скорости, соответствует делению 60 минут или 1 час (60 секунд или 1 минута);
—нанесен красной краской на шкале 2, служит для решения задач, связанных с определением времени полета, пройденного расстояния и путевой скорости, соответствует делению 60 минут или 1 час (60 секунд или 1 минута); —нанесены на шкале 2 и могут использоваться как начальные или конечные штрихи шкалы;
—нанесены на шкале 2 и могут использоваться как начальные или конечные штрихи шкалы; —нанесен на шкале 4, соответствует делению 45° и используется для решения задач, в которые входят тригонометрические функции углов;
—нанесен на шкале 4, соответствует делению 45° и используется для решения задач, в которые входят тригонометрические функции углов; — нанесен на движке под шкалой 7 и служит для решения задач по определению показаний барометрических высотомеров в полете до высоты 12 000 м.
— нанесен на движке под шкалой 7 и служит для решения задач по определению показаний барометрических высотомеров в полете до высоты 12 000 м. — нанесен на шкале 12 и служит для решения задач по определению показаний барометрических высотомеров в полете для высот более 12 000 м.
— нанесен на шкале 12 и служит для решения задач по определению показаний барометрических высотомеров в полете для высот более 12 000 м. — нанесены на шкалах 14 и 15 и служат для обозначения десятичных интервалов шкал, используются для умножения и деления чисел;
— нанесены на шкалах 14 и 15 и служат для обозначения десятичных интервалов шкал, используются для умножения и деления чисел; — деление шкалы 4, используется при решении задач по определению времени разворота самолета на 360°.
— деление шкалы 4, используется при решении задач по определению времени разворота самолета на 360°. десятичный интервал, которым пользуются одновременно со шкалой 1 при умножении и делении безразмерных величин.
десятичный интервал, которым пользуются одновременно со шкалой 1 при умножении и делении безразмерных величин. , если время берется в минутах или часах, либо против индекса
, если время берется в минутах или часах, либо против индекса  , если время берется в секундах.
, если время берется в секундах. до
до  , т. е. являются корнями квадратными величин, нанесенных на шкалах 1 и 5. Шкала 6 служит для решения задач по определению радиуса разворота самолета, для извлечения корней квадратных из чисел и возведения их в квадрат, а также используется при решении комбинированных задач.
, т. е. являются корнями квадратными величин, нанесенных на шкалах 1 и 5. Шкала 6 служит для решения задач по определению радиуса разворота самолета, для извлечения корней квадратных из чисел и возведения их в квадрат, а также используется при решении комбинированных задач. служат для пересчета показаний барометрических высотомеров, построенных на принципе замера статического давления воздуха на высоте полета, в исправленное значение высоты с целью учета методической ошибки высотомера, являющейся следствием того, что фактическая средняя температура столба воздуха не совпадает с расчетной, принятой для построения шкалы высотомера по условиям международной стандартной атмосферы (МСА).
служат для пересчета показаний барометрических высотомеров, построенных на принципе замера статического давления воздуха на высоте полета, в исправленное значение высоты с целью учета методической ошибки высотомера, являющейся следствием того, что фактическая средняя температура столба воздуха не совпадает с расчетной, принятой для построения шкалы высотомера по условиям международной стандартной атмосферы (МСА). служат для пересчета показаний барометрических высотомеров в исправленные значения высоты для высот более 12 000 м с целью учета методической ошибки, являющейся следствием того, что фактическая температура воздуха на высоте полета более 11 000 м не является постоянной и не равна расчетной 56,5°С, принятой для построения шкалы высотомера.
служат для пересчета показаний барометрических высотомеров в исправленные значения высоты для высот более 12 000 м с целью учета методической ошибки, являющейся следствием того, что фактическая температура воздуха на высоте полета более 11 000 м не является постоянной и не равна расчетной 56,5°С, принятой для построения шкалы высотомера. совмещен с делением шкалы 12, равным 11 км. Кроме того, при пересчете высоты полета более 12 000 м по этим шкалам к значению высоты, отсчитанному по шкале 14, необходимо прибавить поправку ΔН = 900 + 20 (t0 + tH) со своим знаком.
совмещен с делением шкалы 12, равным 11 км. Кроме того, при пересчете высоты полета более 12 000 м по этим шкалам к значению высоты, отсчитанному по шкале 14, необходимо прибавить поправку ΔН = 900 + 20 (t0 + tH) со своим знаком. ,
, 
 ,
, шкалы 14 или
шкалы 14 или  шкалы 2 (движок вышел влево), или на единицу меньше, если против множимого было установлено деление 100 шкалы 14 или
шкалы 2 (движок вышел влево), или на единицу меньше, если против множимого было установлено деление 100 шкалы 14 или  шкалы 2 (движок вышел вправо).
шкалы 2 (движок вышел вправо). шкалы 2 (движок вышел влево), или на единицу больше, если отсчет был сделан против деления 100 шкалы 14 или
шкалы 2 (движок вышел влево), или на единицу больше, если отсчет был сделан против деления 100 шкалы 14 или  на деление шкалы 15, соответствующее множимому (рис. 10);
на деление шкалы 15, соответствующее множимому (рис. 10);

 искомое частное.
искомое частное.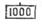 шкалы 14 используются индексы
шкалы 14 используются индексы  шкалы 2 соответственно.
шкалы 2 соответственно.
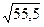 =7,42.
=7,42.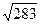 =16,8.
=16,8. = 0,0807.
= 0,0807.
 на деление 100 шкалы 5 (рис. 15);
на деление 100 шкалы 5 (рис. 15);

 против деления шкалы 5, соответствующего заданному числу (рис. 17);
против деления шкалы 5, соответствующего заданному числу (рис. 17);



 искомое частное.
искомое частное.




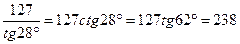

 .
. .
. .
.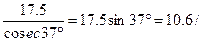 .
.
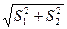 по шкалам 5 и 6, для чего сначала определить
по шкалам 5 и 6, для чего сначала определить  и
и 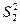 , затем сложить и из суммы извлечь квадратный корень;
, затем сложить и из суммы извлечь квадратный корень;
 по шкале 1 на деление, соответствующее значению 0,017 (рис. 20);
по шкале 1 на деление, соответствующее значению 0,017 (рис. 20); = 165 км; r = 11 км;
= 165 км; r = 11 км;


