
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные типы расчетов на прочностьСтр 1 из 3Следующая ⇒
Пример 1. Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2 Р и 3 Р вдоль продольной оси стержня, показанный на рис.2.1. Определить величину внутренних сил.
Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Qy, Mx и уравновешивая оставшуюся часть, получим: I участок:
Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N. Пример 2. Построить эпюру продольных сил для жестко защемленной балки (рис.2.2.1). Решение: 1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке. 2. Определяем продольную силу
3. По найденным значениям строим эпюру Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.
Рис.2.2.1
Пример 3. Два стержня, соединенные в т. А, находятся под действием силы Р (рис.2.3а). Определить усилия, действующие в стержнях.
Решение. Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n - n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N 1 и N 2 в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис.2.3б). Уравновесим отсеченную часть, запишем уравнения
Решая, из первого уравнения получим
из второго уравнения окончательно имеем
Так как величина силы N 2 < 0, то её направление следует изменить на противоположное (рис.2.3в). Согласно рисунку нормальная сила N 1 растягивает отсеченную часть стержня 1 - она положительна, сила N 2 сжимает отсеченную часть стержня 2 - она отрицательна. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука (
Для обеспечения прочности стержня должно выполняться условие прочности - конструкция будет прочной, если максимальное напряжение ни в одной точке нагруженной конструкции не превышает допускаемой величины, определяемой свойствами данного материала и условиями работы конструкции, то есть
Допускаемое напряжение
где n - коэффициент запаса прочности. Величина коэффициента запаса прочности назначается в пределах n = 1,5... 3, а иногда и более, с учетом многих факторов, в частности, точности принятых расчетных соотношений, условий эксплуатации конструкции, особых требований по безопасности работы, норм, принятых в отрасли промышленности. В машинах и аппаратах химических производств n»1,5. Пример 1. Рассмотрим вал, нагруженный скручивающими моментами Т 1=10 кНм, Т 2=25 кНм, Т 3=35 кН×м (рис.5.2). Решение. Воспользуемся методом сечений. Рассечем участки вала (рис.5.2). Границами участков являются точки приложения скручивающих моментов. Отбросим правую отсеченную часть. Заменим ее крутящим моментом М к. Из уравнения равновесия отсеченной части найдем величину крутящего момента М к, возникающего в сечении.
Рис.5.2 Рис.5.3
I участок
M к1 = 0. II участок
M к2 = T 1 = 10 кНм. III участок
M к3 = T 1 + T 2 = 35 кНм. Для наглядного представления о величине крутящих моментов и характере их распределения по длине вала построим эпюры этих моментов. Построение эпюр крутящих моментов аналогично построению эпюр продольных сил при осевом растяжении-сжатии (рис.5.3). Заметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.
Лекция 6. Плоский изгиб Напряжения и перемещения
Пример 10. Для заданных двух схем балок (рис.6.32) требуется написать выражения
Рис.6.32,а Рис.6.32,б Решение.
Рис.9.4. Таким образом, поставленная задача решена; для нашего стержня наименьшая критическая сила определяется формулой
а изогнутая ось представляет синусоиду
Величина постоянной интегрирования а осталась неопределенной; физическое значение ее выяснится, если в уравнении синусоиды положить
Значит, а — это прогиб стержня в сечении посредине его длины. Так как при критическом значении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб f остался неопределенным. Он должен быть при этом настолько малым, чтобы мы имели право применять приближенное дифференциальное уравнение изогнутой оси, т. е. чтобы Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения
Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения. Это отношение Из последнего выражения видно видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность
Таким образом, если бы площадь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы. Влияние способа закрепления концов стержня. Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при определенном закреплении его концов (шарнирно-опертых). Значит, найденное выражение критической силы справедливо лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня. Закрепление сжатого стержня с шарнирно-опертыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить' к основному случаю. Если повторить весь ход вывода для стержня, жестко защемленного одним концом и нагруженного осевой сжимающей силой на другом конце (Рис.9.5), то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.
Рис.9.5. Расчетная схема стержня с жесткозакрепленным одним концом. Предоставляя право студентам проделать это во всех подробностях самостоятельно, подойдем к выяснению критической силы для этого случая путем следующих простых рассуждений. Пусть при достижении силой Р критического значения колонна будет сохранять равновесие при слабом выпучивании по кривой АВ. Сравнивая два варианта изгиба видим, что изогнутая ось стержня, защемленного одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закрепленными концами. Значит, критическая сила для стойки длиной
Если мы обратимся к случаю стойки, у которой оба конца защемлены и не могут поворачиваться (Рис.9.6), то заметим, что при выпучивании, по симметрии, средняя часть стержня, длиной
Рис.9.6. Расчетная схема с жесткозакреплеными торцами. Поэтому критическая сила для стержня с защемленными концами, длиной
бб Пример 1. Пусть имеется стержень постоянного поперечного сечения, нагруженный силами 2 Р и 3 Р вдоль продольной оси стержня, показанный на рис.2.1. Определить величину внутренних сил.
Стержень может быть разделен на два участка, граничными точками которых являются точки приложения сосредоточенных сил и точка закрепления. Если начало координат расположить на правом конце стержня, а ось z направить справа налево, то, используя метод сечений, рассекая последовательно участки, отбрасывая левую часть, заменяя ее действие внутренними усилиями N, Qy, Mx и уравновешивая оставшуюся часть, получим: I участок:
Как видно, при растяжении в поперечных сечениях стержня возникает только один внутренний силовой фактор - нормальная сила N. Пример 2. Построить эпюру продольных сил для жестко защемленной балки (рис.2.2.1).
Решение: 1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке. 2. Определяем продольную силу
3. По найденным значениям строим эпюру Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.
Рис.2.2.1
Пример 3. Два стержня, соединенные в т. А, находятся под действием силы Р (рис.2.3а). Определить усилия, действующие в стержнях.
Решение. Воспользуемся методом сечений. Рассечем стержни в произвольном месте сечения n - n. Отбросим левую отсеченную часть. Заменим отброшенную часть, приложив усилия N 1 и N 2 в сечениях к правой части. Направление усилий целесообразно выбрать так чтобы они растягивали отсеченные части (рис.2.3б). Уравновесим отсеченную часть, запишем уравнения
Решая, из первого уравнения получим
из второго уравнения окончательно имеем
Так как величина силы N 2 < 0, то её направление следует изменить на противоположное (рис.2.3в). Согласно рисунку нормальная сила N 1 растягивает отсеченную часть стержня 1 - она положительна, сила N 2 сжимает отсеченную часть стержня 2 - она отрицательна. Поэтому можно сделать вывод о равномерном по сечению распределении продольных деформаций, а на основании закона Гука (
Для обеспечения прочности стержня должно выполняться условие прочности - конструкция будет прочной, если максимальное напряжение ни в одной точке нагруженной конструкции не превышает допускаемой величины, определяемой свойствами данного материала и условиями работы конструкции, то есть
Допускаемое напряжение
где n - коэффициент запаса прочности. Величина коэффициента запаса прочности назначается в пределах n = 1,5... 3, а иногда и более, с учетом многих факторов, в частности, точности принятых расчетных соотношений, условий эксплуатации конструкции, особых требований по безопасности работы, норм, принятых в отрасли промышленности. В машинах и аппаратах химических производств n»1,5. Основные типы расчетов на прочность Используя условие прочности (2.1), можно решать следующие основные типы расчетов: Проектировочный расчет - определение по известной нагрузке и допускаемому напряжению размеров поперечного сечения стержня
Проверочный расчет - проверка прочности стержня, т.е. определение по заданным нагрузке и размерам поперечного сечения стержня фактических напряжений и сравнение их с допускаемыми Определение максимальной нагрузки по заданным размерам поперечного сечения и
Определив допускаемую нормальную силу Nmax и установив связь между нормальной силой и нагрузкой с помощью метода сечений, можно определить и максимальную нагрузку Pmax.
|
|||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.08 с.) |
 Решение.
Решение.
 ,
,  ;
;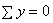 ,
,  ;
; ,
, 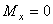
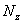 в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
 .
.

 ;
;  .
.
 ,
, ;
;  .
. ) и нормальных напряжений
) и нормальных напряжений  = const. Тогда
= const. Тогда  , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении
, откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении .
. . (2.2)
. (2.2) определяется по формуле
определяется по формуле ,
, - предельное (опасное) для данного материала напряжение, определяется экспериментально при испытании материалов;
- предельное (опасное) для данного материала напряжение, определяется экспериментально при испытании материалов;


 ,
,
 ,
,

 ,
,  для каждого участка в общем виде, построить эпюры
для каждого участка в общем виде, построить эпюры  , найти
, найти  и подобрать: для схемы а) деревянную балку круглого поперечного сечения при
и подобрать: для схемы а) деревянную балку круглого поперечного сечения при  МПа; для схемы б) стальную балку двутаврового поперечного сечения при
МПа; для схемы б) стальную балку двутаврового поперечного сечения при 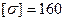 МПа. При М = 20 кН/м, Р = 20 кН, q = 8 кН/м,
МПа. При М = 20 кН/м, Р = 20 кН, q = 8 кН/м,  м,
м,  м,
м,  ,
, 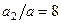 ,
,  .
.

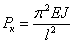

 ; тогда
; тогда 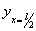 (т. е. посредине длины стержня) получит значение:
(т. е. посредине длины стержня) получит значение:
 было по прежнему мало по сравнению с единицей.
было по прежнему мало по сравнению с единицей. , разделив силу
, разделив силу  на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для
на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для  поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня
поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня  . Тогда
. Тогда
 называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.
называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость. . Так, для стали 3 с пределом прочности
. Так, для стали 3 с пределом прочности  допускаемое напряжение может быть принято
допускаемое напряжение может быть принято 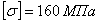 ; критическое же напряжение для стержня с гибкостью
; критическое же напряжение для стержня с гибкостью  при модуле упругости материала
при модуле упругости материала  будет равно
будет равно

 с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине
с одним защемленным, а другим свободным концами будет та,же, что для стойки с шарнирно-опертыми концами при длине  :
: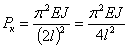
 , будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).
, будет работать в тех же условиях, что и стержень при шарнирно-опертых концах (так как в точках перегиба С и D изгибающие моменты равны нулю, то эти точки можно рассматривать как шарниры).

 .
. .
. .
.


