
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симплекс-метод. Допустимый вид системы ограничений, допустимый базис, условие неотрицательности свободных членов.
Допустимый вид системы ограничений: Какие-то из неизвестных должны быть выражены через остальные неизвестные, причем свободные члены этих выражений неотрицательны. Пример: x1 = -2x4 + 7x5 + 5 x2 = 3x4 + 6x5 + 4 x3 = -x4 + 2x5 Допустимый базис: Все свободные члены в правых частях неотрицательны Для решения задач линейного программирования симплекс-методом следует выполнить ряд подготовительных операций. 1. Привести задачу к каноническому виду. 2. Преобразовать систему ограничений (уравнений) к специальному виду, в котором переменные разделены на базисные и свободные, а соответствующее базисное решение – неотрицательное (оно называется допустимым базисным решением или опорным решением). x1 + a1 r+1 xr+1 + … + a1 n xn = b1 x2 + a2 r+1 xr+1 + … + a2 n xn = b2 (1) ………………………………………………………. xr + ar r+1 xr+1 + … + ar n xn = br где x1, x2, ….., xr – базисные переменные, xr+1, xr+2, ….., xn – свободные переменные bi ≥ 0, I = 1, 2, …, r 3. Исключить из целевой функции базисные переменные с помощью (1) и записать ее в виде f + cr+1 xr+1 + … + cnxn = c0 (2) Коэффициенты, ci, i = r + 1, …, n называются оценками соответствующих переменных xr+1, xr+2, …, xn Из (1), (2) следует, что на допустимом базисном решении X баз = (c 1; c 2; …; cr; 0; 0; …; 0) *принадлежит* R n целевая функция принимает значение f (xбаз) = c0
После выполнения подготовительного этапа заполняется начальная симплекс-таблица:
Здесь и ниже используются следующие сокращения: 1. Б.н. – базисные неизвестные. 2. С.ч. – свободные члены. Таблица соответствует системе уравнений (1) с присоединенной целевой функцией (2). Последняя строка таблицы называется строкой оценок. Пусть решается задача о нахождении минимума функции f. Тогда цель дальнейших симплексных преобразований таблиц состоит в нахождении новых допустимых базисных решений, на которых значение целевой функции уменьшается (или не увеличивается). Алгоритм симплексных преобразований заключается в следующем.
а) Если в строке оценок среди чисел c k (k ≠ 0) имеется хотя бы одна положительная (например c p), а в соответствующем столбце (разрешающем столбце) хотя бы один положительный элемент, то решение может быть улучшено. Среди указанных положительных элементов столбца в качестве разрешающего элемента aip выбирается тот, которому отвечает минимальное отношение bi / aip. Если имеется несколько элементов с подобным свойством, то в качестве разрешающего выбирается любой из них. В таблице таким элементом является aqp. Далее над таблицей проводятся элементарные преобразования: переменная xp становится базисной, а xq – свободной. На новом базисном решении значение целевой функции не увеличивается, и снова анализируется строка оценок. б) Если в строке оценок нет положительных чисел, то оптимальное решение найдено. в) Если в строке оценок есть положительное число, а в соответствующем ей столбце нет положительных элементов, то задача ЛП не имеет решения. В задаче о нахождении минимума функции это обозначается так: min f = −∞. г) Если в последней строке нет положительных оценок, но при этом имеются свободные переменные, равные нулю, то задача имеет, по крайней мере, одно альтернативное решение (чтобы его получить, следует сделать еще одно преобразование, выбрав разрешающий столбец с нулевой оценкой). Как правило, множество оптимальных решений совпадает с выпуклой оболочкой всех альтернативных (базисных) решений. Исключением является случай, когда в процессе перебора альтернативных решений возникает нулевая оценка, такая, что в соответствующем столбце нет положительных чисел. При решении задачи о поиске максимума функции f алгоритм меняется только в том, что разрешающий столбец выбирается по отрицательной оценке в последней строке. 15. Симплекс-таблица. Строка оценок. Условие оптимальности базисного решения. Условие неограниченности целевой функции. Условие существования альтернативного решения. Примеры. Строка оценок – последняя строка симплекс-таблицы (коэффициенты целевой функции)
Условие оптимальности базисного решении: Все коэффициенты при свободных неизвестных в выражении для f неотрицательны Условие неограниченности целевой функции: Базисное решение является оптимальным, если все коэффициенты в строке оценок положительны (в задаче на max) или отрицательны (в задаче на min). Если в задаче на максимум (минимум) в строке оценок есть отрицательный (положительный) элемент, а в соответствующем ей столбце нет положительных элементов, то ЗЛП неразрешима и fmax=+ Условие существования альтернативного решения: Если в строке оценок в задаче на максимум (минимум) нет отрицательных (положительных) оценок, но при этом имеются свободные переменные, равные 0, то задача имеет как минимум одно альтернативное решение. После выполнения подготовительного этапа заполняется начальная симплекс-таблица:
aq p -> bi / aip -min Здесь и ниже используются следующие сокращения: 1. Б.н. – базисные неизвестные. 2. С.ч. – свободные члены. Таблица соответствует системе уравнений (1) с присоединенной целевой функцией (2). Последняя строка таблицы называется строкой оценок. Пусть решается задача о нахождении минимума функции f. Тогда цель дальнейших симплексных преобразований таблиц состоит в нахождении новых допустимых базисных решений, на которых значение целевой функции уменьшается (или не увеличивается). Алгоритм симплексных преобразований заключается в следующем. а) Если в строке оценок среди чисел c k (k ≠ 0) имеется хотя бы одна положительная (например c p), а в соответствующем столбце (разрешающем столбце) хотя бы один положительный элемент, то решение может быть улучшено. Среди указанных положительных элементов столбца в качестве разрешающего элемента aip выбирается тот, которому отвечает минимальное отношение bi / aip. Если имеется несколько элементов с подобным свойством, то в качестве разрешающего выбирается любой из них. В таблице таким элементом является aqp. Далее над таблицей проводятся элементарные преобразования: переменная xp становится базисной, а xq – свободной. На новом базисном решении значение целевой функции не увеличивается, и снова анализируется строка оценок. б) Если в строке оценок нет положительных чисел, то оптимальное решение найдено. в) Если в строке оценок есть положительное число, а в соответствующем ей столбце нет положительных элементов, то задача ЛП не имеет решения. В задаче о нахождении минимума функции это обозначается так: min f = −∞. г) Если в последней строке нет положительных оценок, но при этом имеются свободные переменные, равные нулю, то задача имеет, по крайней мере, одно альтернативное решение (чтобы его получить, следует сделать еще одно преобразование, выбрав разрешающий столбец с нулевой оценкой). Как правило, множество оптимальных решений совпадает с выпуклой оболочкой всех альтернативных (базисных) решений. Исключением является случай, когда в процессе перебора альтернативных решений возникает нулевая оценка, такая, что в соответствующем столбце нет положительных чисел.
При решении задачи о поиске максимума функции f алгоритм меняется только в том, что разрешающий столбец выбирается по отрицательной оценке в последней строке.
16. Теорема о конечности симплекс-алгоритма (без доказательства). Если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Последнее всегда может быть получено с помощью симплекс-метода, причем начинать можно с любого исходного базиса. Эту теорему часто называют теоремой о конечности симплекс-алгоритма. И, действительно, в ней утверждается, что если ЗЛП разрешима, то, взяв любой исходный базис и выбирая последовательность разрешающихся элементов подходящим образом, мы всегда придем – после конечного числа шагов – к базисному оптимальному решению.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.158 (0.012 с.) |
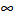 (fmin=-
(fmin=- 


