
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы.Стр 1 из 5Следующая ⇒
Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы. Для любой неотрицательной матрицы А=>0 существует собственное значение λА=>0 (называемое числом Фробениуса) такое, что λА=>|λ| для любого собственного значения λ матрицы А. Кроме того, существует неотрицательный собственный вектор
Вектор валового выпуска, вектор конечного потребления, матрица прямых затрат.
А = Уравнение межотраслевого баланса. Модель Леонтьева. Продуктивная матрица.
Первый и второй критерии продуктивности. 1-ый кр. прод: Матрица А=>0 продуктивна тогда и только тогда, когда матрица
2-ой кр. прод: Неотрицательная квадратная матрица А продуктивна тогда и только тогда, когда её число Фробениуса меньше единицы.
5. Докажите, что матрица A ≥ 0 продуктивна тогда и только тогда, когда матрица Пусть существует
Докажите, что если неотрицательная квадратная матрица продуктивна, то ее число Фробениуса меньше 1. Матрица А≥0 называется продуктивной, если для любого вектора
Пусть матрица А – неотрицательна и продуктивна. Тогда для любого неотрицательного вектора
Пусть
Примеры ЗЛП. Задача о банке, задача о диете, задача об использовании ресурсов. 1) Задача о банке. Пусть собственные средства банка в сумме с депозитами составляют S млн долл. Часть этих средств, но не менее K млн долл., должна быть размещена в кредитах. Кредиты являются неликвидными активами банка, так как в случае непредвиденной потребности в наличности обратить кредиты в деньги без существенных потерь невозможно. Другое дело ценные бумаги (особенно государственные). Их можно в любой момент продать, получив некоторую прибыль или, во всяком случае, без большого убытка. Поэтому существует правило, согласно которому коммерческие банки должны покупать в определенной пропорции ликвидные активы – ценные бумаги, чтобы компенсировать неликвидность кредитов. В нашем примере ликвидное ограничение таково: ценные бумаги должны составлять не менее p % средств, размещенных в кредитах и ценных бумагах. Пусть x – средства (млн долл.), размещенные в кредитах, y – средства, вложенные в ценные бумаги. Имеем следующую систему линейных ограничений: 1) x+y ≤ S – балансовое ограничение; 2) x+K – кредитное ограничение; 3) y ≥0,01 p(x + y) – ликвидное ограничение; 4) x ≥0, y ≥0. Цель банка состоит в том, чтобы получить максимальную прибыль от кредитов и ценных бумаг: Так как кредиты менее ликвидны, чем ценные бумаги, то обычно 2) Задача о диете. Известно, что 1 кг яблок стоит 30 руб., а 1 кг абрикосов 60 руб. Сколько яблок и абрикосов должен потреблять человек в сутки, чтобы получить не менее 70 мг витамина С и не менее 2 мг витамина А при минимальных затратах на яблоки и абрикосы? Содержание витаминов А и С в яблоках и абрикосах указано в таблице.
Где
Общая форма Задача о диете: Пусть имеется 2 вида продуктов П1 и П2, содержащих питательные вещества А,В,С. В 1кг продуктов П1 и П2 содержится определенное количество вещества того или иного вида.
a,b,c- ежесуточное потребление А, В и С соответственно s1,s2- стоимость П1 и П2 соответственно Тогда целевая функция f=s1x1+s2x2-->min Система ограничений: Задача об использовании ресурсов: пусть R1, R2,R3 – наличные ресурсы b1,b2,b3 – количество ресурсов R1,R2,R3 соответственно Т1,Т2 – выпускаемые товары aij- число единиц ресурса, необходимых для выпуска 1 единицы товара с1,с2 – доход от продажи товаров Т1, Т2 соответственно х1, х2 – количество товаров Т1 и Т2 соответственно общее количество ресурса R1, используемого при выпуске обоих товаров, равное Тогда целевая функция f=c1x1+c2x2--->max система ограничений:
Другие задачи ЗЛП: - задача об оптимальном портфеле ценных бумаг - задача о заготовках - транспортная задача Каноническая и стандартная формы ЗЛП. Приведение ЗЛП к стандартному и каноническому виду. Примеры. Каноническая форма ЗЛП предполагает нетривиальную[3] систему ограничений, которые являются уравнениями. Стандартная форма ЗЛП предполагают эту систему, но уже только с неравенствами. Любая ЗЛП может быть сведена как к канонической, так и к стандартной форме.
Пример 1 Привести данную ЗЛП к каноническому виду
Где Пример 2. Привести данную ЗЛП к стандартному виду
Преобразуем систему уравнений методом Гаусса к виду
с базисными неизвестными Учитывая неотрицательность неизвестных, получаем систему неравенств
Паутинная модель рынка. Это модель поиска равновесной цены. Спрос и предложение - линейные ф-ии. Dt= a – bpt, s = m + npt-1, a,b,m,n – положит., действ. Числа. St=Dt: a-m = bpt+npt-1. - линейное разностное уравнение 1-го порядка с пост. коэфф. В качестве частного решения: pt =
Решая характ-е ур-е bλ + n = 0, λ = -n/b. => Pt= C1(-n/b)t + Таким образом динамика цен носит колебательный характер. N<b - сходится к равновесному состоянию n>b – удаляться от равновесного состояния n=b – циклические колебания цены относительно равновесного состояние.
Теорема Фробениуса-Перрона. Определение числа и вектора Фробениуса неотрицательной матрицы. Для любой неотрицательной матрицы А=>0 существует собственное значение λА=>0 (называемое числом Фробениуса) такое, что λА=>|λ| для любого собственного значения λ матрицы А. Кроме того, существует неотрицательный собственный вектор
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 891; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.131.168 (0.022 с.) |
 А=>0, соответствующий собственному значению λА и называемый вектором Фробениуса. Причём, если А>0, то λА>0 и
А=>0, соответствующий собственному значению λА и называемый вектором Фробениуса. Причём, если А>0, то λА>0 и 

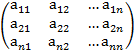 - матрица прямых затрат (матрица Леонтьева)
- матрица прямых затрат (матрица Леонтьева) – уравнение межотраслевого баланса (уравнение Леонтьева). Межотраслевой баланс — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Основная задача межотраслевого баланса состоит в нахождении такого вектора валового выпуска
– уравнение межотраслевого баланса (уравнение Леонтьева). Межотраслевой баланс — экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Основная задача межотраслевого баланса состоит в нахождении такого вектора валового выпуска  , который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта
, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта  . Зная матрицу А и вектор
. Зная матрицу А и вектор  . Матрица А=>0 называется продуктивной, если для любого вектора
. Матрица А=>0 называется продуктивной, если для любого вектора  существует решение
существует решение  уравнения Леонтьева.
уравнения Леонтьева. существует и неотрицательна.
существует и неотрицательна. − существует и неотрицательна (первый критерий продуктивности).
− существует и неотрицательна (первый критерий продуктивности). =>0, тогда x=(E-A)-1y, где оба множителя >0, следовательно, x=>0, значит матрица продуктивна. Пусть А продуктивна. (E-A)x=e1, значит с1=>0, (E-A)x=e2, значит с2=>0, следовательно, (с1,с2,cn)=C=>0. (E-A)C=E=>C=(E-A)-1=>0
=>0, тогда x=(E-A)-1y, где оба множителя >0, следовательно, x=>0, значит матрица продуктивна. Пусть А продуктивна. (E-A)x=e1, значит с1=>0, (E-A)x=e2, значит с2=>0, следовательно, (с1,с2,cn)=C=>0. (E-A)C=E=>C=(E-A)-1=>0 ≥0 существует решение
≥0 существует решение 
 и учитывая, что
и учитывая, что , то получим
, то получим

 >0,
>0,  >0,
>0,  >0. Поэтому из последнего равенства вытекает, что
>0. Поэтому из последнего равенства вытекает, что  <1.
<1. → max при условиях 1) – 4), где
→ max при условиях 1) – 4), где  – доходность кредитов,
– доходность кредитов,  – доходность ценных бумаг.
– доходность ценных бумаг. . Мы пришли к задаче линейного программирования с ограничениями 1) – 4) и целевой функцией f, которую требуется максимизировать.
. Мы пришли к задаче линейного программирования с ограничениями 1) – 4) и целевой функцией f, которую требуется максимизировать. при
при
 - суточое потребление яблок и абрикосов в кг
- суточое потребление яблок и абрикосов в кг

 , не должно превосходить bi , т.е. должны выполняться неравенства
, не должно превосходить bi , т.е. должны выполняться неравенства  , i=1,2,3
, i=1,2,3






 , и свободными неизвестными
, и свободными неизвестными  .
.
 = const. Тогда:
= const. Тогда: .
. .
.


