
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение электронов по энергии в зоне проводимости
В зоне проводимости громадное количество электронов и громадное количество подуровней энергии. Классическое распределение Максвелла для энергий свободных частиц дает для средней кинетической энергии величину, равную 3kT/2. Но это не применимо для электронов в металлах. Следует учесть принцип Паули. Для электронов число их n(E)dE c энергиями в диапазоне от E до E+dE равно
где s(E)dE - число состояний c энергиями в диапазоне от E до E+dE в единице объема, а f(E) - вероятность, что состояние с энергией E занято. Энергия E отсчитывается от дна зоны проводимости. Функция f(E) получена Ферми и носит его имя. Займемся плотностью состояний s(E). Рассмотрим металлический образец в виде куба со стороной L. Можно считать, что электроны проводимости находятся в трехмерной прямоугольной потенциальной яме шириной L (см. лекцию). В этом случае энергия частицы определяется тремя квантовыми числами n1, n2 и n3.
В действительности для каждого значения E имеем два состояния с противоположными направлениями спинов. Значение функции s(E) нам надо знать для энергий, далеких от энергии основного состояния (n1=n2=n3=1). Для этих энергий дискретностью квантовых чисел n можно пренебречь. Представим пространство квантовых чисел, где по осям отложены n1, n2 и n3. Каждой точке этого пространства соответствует два состояния. Брать надо только положительные значения n, т.к. отрицательные дают то же самое значение энергии. В этом пространстве все состояния с энергией, меньшей E, занимают 1/8 объема шара радиуса n, где n
Используя выражения для E и n, получим выражение для числа таких состояний PE
Плотность состояний s(E)
Обратим внимание на то, что число состояний в единице объема, приходящееся на единичный интервал энергий, s(E) ~ E1/2. Теперь займемся функцией Ферми f(E). Вид ее
где k - постоянная Больцмана, T - абсолютная температура, E0 - параметр, имеющий размерность энергии и называемый энергией Ферми. Вид этого распределения показан на рис.7 для двух случаев: a) - температура T → 0; b) - T > 0. Из рисунка a) становится понятным смысл энергии Ферми: E0 - это такая энергия, что все состояния при T = 0 с E < E0 заняты. Выше этой энергии все состояния свободны. Из рисунка b) видно, что изменение вероятности от 1 до 0 происходит в области шириной порядка kT вблизи энергии Ферми E0.
При комнатной температуре kT ~ 0.025 эВ, тогда как E0 составляет для металлов единицы эВ. Действительно, интегрирование плотности распределения s(E) по энергии от 0 до E0 дает число электронов в единице объема металла в зоне проводимости, которое можно определить через число Авогадро NA, массовое число A, плотность ρ и число валентных электронов ZV
Для натрия, например, E0 = 3.2 эВ, для меди - 7.1 эВ. Экспериментально эту величину определяют по ширине линии рентгеновского спектра, соответствующей переходу валентных электронов в состояние 1s, расщепление энергии которых чрезвычайно мало. Электропроводность металлов Начнем с классического рассмотрения. Как известно, плотность тока j= envдр, где e - заряд электрона, n - концентрация электронов, vдр - скорость дрейфа в электрическом поле. Электроны в металле претерпевают соударения, и после каждого из соударений величина скорости v уже почти не зависит от скорости до соударения. Приложенное электрическое поле почти не влияет на величину скорости v, но зато это влияние имеет направленный характер, характеризуемый скоростью дрейфа vдр. Величину последней можно оценить из следующих соображений. В электрическом поле напряженностью E каждый электрон приобретает ускорение e E /m, изменение скорости за время t между соударениями e E t/m. Среднее изменение скорости между соударениями и есть скорость дрейфа
где λ - длина свободного пробега, v - скорость теплового движения электрона, и проведено усреднение v с учетом максвелловского распределения по скоростям. Для проводимости σ = j/ E получаем
Приходит к выводу, что удельное сопротивление ρ, которое обратно пропорционально проводимости, меняется с температурой как ρ ~ T1/2. Однако известно, что удельное сопротивление линейно растет с температурой. Для правильной интерпретации экспериментальных результатов следует учесть квантовые эффекты. Квантово-механический подход. Существенны распределение электронов по энергии в зоне проводимости и принцип Паули: под действием электрического поля E из всего множества электронов изменить свою энергию могут только те, чьи энергии близки к энергии Ферми E0. Только здесь имеются свободные состояния. В формуле для скорости дрейфа в качестве скорости v следует подставить
v0 - скорость электронов с энергией Ферми E0. Зависимость скорости дрейфа от температуры в металле остается в длине свободного пробега λ. При отсутствии тепловых колебаний атомов и нарушений структуры кристалла длина пробега стремилась бы к бесконечности. При не слишком низких температурах колебательная энергия прямо пропорциональна температуре T. Колебания имеют малую амплитуду, хорошо работает модель гармонического осциллятора. В этом случае квадрат амплитуды колебаний пропорционален колебательной энергии, а, следовательно, и температуре T. Сечение рассеяния электронов σрасс пропорционально квадрату амплитуды колебаний и поэтому температуре T. Длина свободного пробега λ
В итоге удельное сопротивление металла пропорционально температуре T, что и наблюдается на опыте. В действительности (см. рис.8) удельное сопротивление обычных металлов при T → 0 стремится к постоянной величине, называемой остаточным сопротивлением. Оно обусловлено примесями и нарушениями кристаллической структуры. Эти помехи движению электронов не зависят от температуры. Теплоемкость Классическое рассмотрение приводит к теплоемкости, не зависящей от температуры Cv = 3R, где R =8314 Дж/(кг-атом·град).
Она получается в предположении, что средняя кинетическая энергия атома равна 3kT/2 и средняя потенциальная энергия колеблющихся атомов имеет то же значение. Полная энергия каждого атома равна, следовательно, 3kT, а для килограмм-атома - 3RT. Соотношение для теплоемкости получается просто дифференцированием по T. Точная классическая теория учитывает связь атомов в кристалле, и рассматривает колебания как суперпозицию волн. Энергия кристалла представляется как сумма энергий всех акустических волн. Результат получается тот же 3R (закон Дюлонга и Пти). Эта простая теория удовлетворительно описывает явления при высоких температурах, но не применима для низких (рис.9), где теплоемкость зависит от температуры и много меньше по значению. Квантовая теория теплоемкости началась с теории А. Эйнштейна. Он предположил, что атомы кристалла можно представить набором независимых гармонических осцилляторов, колеблющихся с одной частотой υ. Энергия осциллятора квантована E = (n+1/2)hυ (см. лекцию). При температуре T осцилляторы находятся в возбужденных состояниях с различными квантовыми числами n, так что среднюю энергию осциллятора можно представить в виде произведения энергии кванта и среднего значения квантового числа
При высоких температурах и hυ << kT эта формула дает (экспоненту разлагаем в ряд и ограничиваемся двумя членами разложения) ε ~ kT, что приводит к Cv = const. В области низких температур, где hυ >> kT, получается
Теплоемкость убывает, но убывает по экспоненциальному закону, тогда как согласно экспериментальным данным теплоемкость убывает по степенному закону. Такое расхождение теории с опытом вызвано предположением о существовании независимых частиц - гармонических осцилляторов.
Следующий шаг в теории теплоемкости сделал П. Дебай. Он учел, что колебания атомов в кристаллической решетке не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных между собой атомов, обладающих 3N степенями свободы. Каждая степень свободы (нормальное колебание) может быть представлена как гармонический осциллятор, средняя энергия которого ε (формула выше). Из-за связи между атомами частоты нормальных колебаний уже не совпадают между собой. Взаимодействие атомов приводит к тому, что колебание, возникшее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Эта волна, дойдя до границы кристалла, отражается. При наложении прямой и отраженной волн образуется стоячая волна, которой соответствует некоторое нормальное колебание кристаллической решетки. Число dN нормальных колебаний, то есть стоячих волн, в интервале частот от υ до υ+dυ велико, поэтому суммирование в выражении для внутренней энергии системы может быть заменено интегрированием:
Математический расчет числа нормальных колебаний приводит к следующему результату для теплоемкости твердого тела
Под интегралом через x обозначено отношение x = hυ/kT. Параметр θD называется дебаевской температурой. Он находится из равенства kθD = hυмакс, где υмакс - максимальная частота нормальных колебаний в кристалле, которая является функцией скорости звука v в среде и концентрации атомов. При низких температурах T << θD верхний предел интеграла будет очень большим, так что его можно приближенно положить равным бесконечности. Тогда интеграл будет представлять собой число, и теплоемкость окажется пропорциональной кубу температуры Cv ~ (T/θD)3, что соответствует экспериментальным данным. При высоких температурах T >> θD экспонента в числителе приближенно равна единице, а экспоненту в знаменателе можно разложить в ряд Тейлора ex ≈ 1+x и приходим закону Дюлонга и Пти
Дебаевские температуры θD для некоторых веществ
Как видим из таблицы, квантовые свойства для многих веществ проявляются и при комнатных температурах.
На первый взгляд удивительно, что теория Дебая приводит к правильным результатам без учета вклада электронов в теплоемкость. Электронов гораздо больше, чем ядер. С ростом температуры тела вместе с увеличением амплитуды колебаний ионов в решетке должна расти и кинетическая энергия электронов проводимости, а значит, они должны давать вклад в суммарную теплоемкость металла. Если бы электроны вели себя как классические свободные частицы идеального газа, и каждый из них делал бы вклад в теплоемкость независимо от остальных, то этот вклад составлял бы 3kT/2. Для теплоемкости при высоких температурах T >> θD вместо закона Дюлонга и Пти имели бы Cv = (3+3/2)R. Однако эксперименты показали, что в действительности теплоемкость металлов при высоких температурах мало отличается от теплоемкости диэлектриков. Следовательно, оценка вклада электронов проводимости в удельную теплоемкость не может быть проведена на основе классической теории. На самом деле бо́льшая часть электронов проводимости при повышении температуры не может изменить своего состояния (см. выше рассуждения, касаающиеся электрической проводимости). Приобрести дополнительную энергию могут только электроны с энергией вблизи энергии Ферми E0. Доля таких порядка kT/E0 << 1. Обнаружить этот вклад можно только вблизи абсолютного нуля и при весьма высоких температурах, когда теплоемкость решетки становится постоянной, а электронная продолжает расти. Явление сверхпроводимости
Удивительное явление, от открытия которого до создания теории прошло около 50 лет. В 1911 году голландский физик Х. Камерлинг-Оннес открыл это явление. Он проводил измерения электрического сопротивления ртути при низких температурах. Оннес хотел выяснить, сколь малым может стать сопротивление вещества электрическому току, если максимально очистить вещество от примесей и максимально уменьшить температуру (искал величину остаточного сопротивления; см. рис.8). Результат этого исследования оказался неожиданным: при температуре ниже 4,15 К сопротивление почти мгновенно исчезло. График такого поведения сопротивления в зависимости от температуры приведен на рисунке слева. В 1913г. Х. Камерлинг-Оннесу присуждена нобелевская премия:
1913
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.42.94 (0.024 с.) |






 Рис.7 Распределение Ферми
Рис.7 Распределение Ферми



 Рис.8 Зависимость сопротивления от температуры
Рис.8 Зависимость сопротивления от температуры

 Рис.9 Зависимость теплоемкости от температуры
Рис.9 Зависимость теплоемкости от температуры





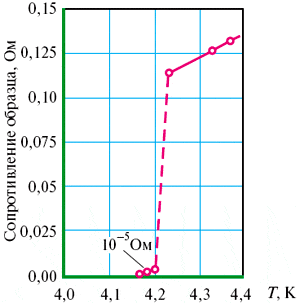 Рис.10 Зависимость сопротивления Pb от температуры (рисунок из работы [5])
Рис.10 Зависимость сопротивления Pb от температуры (рисунок из работы [5])




