
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитное поле поверхностного
Электрического тока Рассмотрим задачу о возбуждении электромагнитного поля сторонним электрическим током, протекающим по листу бесконечно малой толщины. По обе стороны от этого, так называемого листа тока - неограниченное однородное изотропное пространство. Пусть амплитудное распределение тока на плоскости - равномерное, а фаза меняется по линейному закону. Задачу будем решать в прямоугольной системе координат. Предположим, что лист тока совпадает с плоскостью XOY (рис.1.2). Тогда комплексная амплитуда вектора поверхностной плотности электрического тока может быть представлена в следующем виде:
где Требуется определить электромагнитное поле, возбуждаемое током (1.3.1). Для решения задачи воспользуемся граничным условием для касательных составляющих вектора напряжённости магнитного поля: касательная составляющая вектора
где Так как условия возбуждения поля в областях z>0 и z<0 одинаковы, то волны в этих областях движутся в направлениях, симметричных относительно плоскости z=0. При этом должны выполняться следующие условия:
где С учётом антисимметрии поперечных составляющих магнитного поля (1.3.3) граничное условие (1.3.2) можно записать в виде:
Переходя к комплексным амплитудам и подставляя в (1.3.4) выражение для тока (1.3.1), получим:
Раскрыв в (1.3.5) векторное произведение
Теперь, когда магнитное поле у поверхности листа тока найдено, определим магнитное поле в пространстве выше листа (z>0) и ниже его (z<0). Поскольку задача для обеих областей решается одинаково, в дальнейшем будем определять поле только в области z>0. Для определения магнитного поля в области вне протекания токов воспользуемся однородным волновым уравнением для вектора напряжённости магнитного поля
Однородное волновое уравнение, будучи записано в скалярной форме, равносильно трём скалярным уравнениям относительно составляющих Найдём сначала решение скалярного волнового уравнения относительно составляющей
Будем решать уравнение (1.3.7) методом разделения переменных. Для этого представим
Подставив (1.3.8) в уравнение (1.3.7), получим:
где для упрощения записи введены обозначения: Разделим каждый член уравнения (1.3.9) на
Из полученного выражения следует, что каждый член его кроме свободного члена зависит только от одного аргумента и равен некоторой константе. Обозначив эти константы через
Это позволит разбить уравнение (1.3.10) на три независимых уравнения а) б) в) В общем случае каждое из уравнений (1.3.11) является однородным волновым уравнением, общее решение которого представляет собой суперпозицию двух волн, одна из которых распространяется в положительном направлении, а другая - в отрицательном направлении оси X, Y или Z, соответственно. Однако, в связи с тем, что в рассматриваемой задаче изменение поля
где A и B - некоторые постоянные амплитудные коэффициенты. При решении уравнения (1.3.11,в) относительно функции
где C - амплитудный множитель. В соответствии с выражением (1.3.10,а) величина
При этом электромагнитное поле вдоль оси Z будет иметь характер волн, распространяющихся в положительном направлении оси Z, если В случае, когда
Выбор знака в выражении (1.3.15) осуществляется таким образом, чтобы экспоненциальный множитель в (1.3.13) соответствовал затухающей волне. Поэтому отрицательный знак перед мнимой единицей в (1.3.15) соответствует волне, затухающей в положительном направлении оси Z, а положительный знак - волне, затухающей в противоположном направлении. Подставив (1.3.12) и (1.3.13) в (1.3.8), получим общее решение для
где Задание 1.3.1 Воспользовавшись изложенным выше методом, решить скалярные волновые уравнения относительно составляющих Для определения электрического поля в области вне источника воспользуемся однородным волновым уравнением для вектора напряжённости электрического поля
Задание 1.3.2 Воспользовавшись изложенным выше методом решения скалярных волновых уравнений, определить выражения для составляющих электрического поля Нетрудно убедиться, что общий вид полученных решений для составляющих электромагнитного поля в области вне источника будет следующим:
В выражениях (1.3.17) Из граничного условия (1.3.6) мы можем определить амплитуды составляющих
Тогда эти две составляющие электромагнитного поля листа электрического тока будут иметь следующий вид:
Для определения остальных составляющих ( 1. Задание 1.3.3 Записать систему уравнений (1.3.20) в координатной форме записи, в прямоугольной системе координат. Воспользоваться для этого известной формулой векторного анализа:
Так как составляющие электромагнитного поля листа тока описываются уравнениями (1.3.17), нетрудно показать, что, продифференцировав их по x,y и z, получим следующие выражения:
Задание 1.3.4 Показать, что составляющие электромагнитного поля
(1.3.23)
Указание: воспользоваться системой уравнений, полученной в результате выполнения задания 1.3.3, учесть выражения (1.3.22) и учесть, что
Задание 1.3.5 Записать выражения для мгновенных комплексов составляющих электромагнитного поля, возбуждаемого листом электрического тока.
|
||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 244; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.40.207 (0.031 с.) |
 (1.3.1)
(1.3.1) - комплексная начальная амплитуда тока;
- комплексная начальная амплитуда тока; 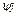 - начальная фаза тока (в дальнейшем примем
- начальная фаза тока (в дальнейшем примем  )
) при переходе через плоскость
при переходе через плоскость  меняется скачком, величина которого равна поверхностной плотности тока, протекающего по плоскости
меняется скачком, величина которого равна поверхностной плотности тока, протекающего по плоскости  :
: , (1.3.2)
, (1.3.2) - нормаль к границе раздела,
- нормаль к границе раздела,  и
и  - касательные составляющие вектора
- касательные составляющие вектора  у граничной поверхности, выше её (z=+0) и ниже её (z=-0) (рис.1.2).
у граничной поверхности, выше её (z=+0) и ниже её (z=-0) (рис.1.2). (1.3.3)
(1.3.3) ,
, ,
,  - поперечные относительно направления распространения составляющие электромагнитного поля в области z>0, а
- поперечные относительно направления распространения составляющие электромагнитного поля в области z>0, а  ,
,  - поперечные составляющие в области z<0.
- поперечные составляющие в области z<0. (1.3.4)
(1.3.4) (1.3.5)
(1.3.5) , определим составляющие вектора напряжённости магнитного поля у поверхности листа тока (z=+0):
, определим составляющие вектора напряжённости магнитного поля у поверхности листа тока (z=+0): (1.3.6)
(1.3.6) .
. .
. :
: (1.3.7)
(1.3.7) в виде произведения трёх функций, каждая из которых зависит только от одной переменной:
в виде произведения трёх функций, каждая из которых зависит только от одной переменной: (1.3.8)
(1.3.8) , (1.3.9)
, (1.3.9) ;
;  ;
;  .
. . Уравнение (1.3.9) примет следующий вид:
. Уравнение (1.3.9) примет следующий вид:
 (1.3.10)
(1.3.10) ,
,  ,
,  , соответственно, представим свободный член
, соответственно, представим свободный член  в уравнении (1.3.10) в виде суммы трёх независимых величин:
в уравнении (1.3.10) в виде суммы трёх независимых величин: (1.3.10,а)
(1.3.10,а)
 (1.3.11)
(1.3.11)
 вдоль осей X и Y определяется заданным законом изменения тока (1.3.1), уравнения (1.3.11,а) и (1.3.11,б) будут иметь решения в виде волн, распространяющихся только в положительном направлении осей X и Y:
вдоль осей X и Y определяется заданным законом изменения тока (1.3.1), уравнения (1.3.11,а) и (1.3.11,б) будут иметь решения в виде волн, распространяющихся только в положительном направлении осей X и Y: ,
,  , (1.3.12)
, (1.3.12) необходимо учесть, что, согласно теореме единственности решения уравнений электродинамики, поля, возбуждаемые источником в виде тока, текущего по плоскости XOY, должны представлять собой волны, уходящие от источника, или поля, убывающие при удалении от источника на бесконечность вдоль оси Z. Поэтому в области z>0 решение уравнения (1.3.11,в) будет иметь следующий вид:
необходимо учесть, что, согласно теореме единственности решения уравнений электродинамики, поля, возбуждаемые источником в виде тока, текущего по плоскости XOY, должны представлять собой волны, уходящие от источника, или поля, убывающие при удалении от источника на бесконечность вдоль оси Z. Поэтому в области z>0 решение уравнения (1.3.11,в) будет иметь следующий вид: , (1.3.13)
, (1.3.13) может иметь действительное значение, если
может иметь действительное значение, если  . Тогда
. Тогда (1.3.14)
(1.3.14) , или волн, распространяющихся в противоположную сторону, при
, или волн, распространяющихся в противоположную сторону, при  .
. , выражение (1.3.14) примет следующий вид:
, выражение (1.3.14) примет следующий вид: (1.3.15)
(1.3.15) составляющей магнитного поля в области z>0:
составляющей магнитного поля в области z>0: , (1.3.16)
, (1.3.16) - неизвестная амплитуда.
- неизвестная амплитуда. и
и  .
. . Представим это уравнение в скалярной форме, в виде трёх скалярных уравнений относительно
. Представим это уравнение в скалярной форме, в виде трёх скалярных уравнений относительно  .
. в области вне источника.
в области вне источника. (1.3.17)
(1.3.17)
 и
и  - неизвестные комплексные амплитуды составляющих электромагнитного поля. Для определения их обратимся к исходным условиям задачи. Так как в рассматриваемом случае предполагается, что среда в областях z>0 и z<0 потерями не обладает, то, следовательно,
- неизвестные комплексные амплитуды составляющих электромагнитного поля. Для определения их обратимся к исходным условиям задачи. Так как в рассматриваемом случае предполагается, что среда в областях z>0 и z<0 потерями не обладает, то, следовательно,  и
и  - некоторые постоянные величины.
- некоторые постоянные величины. и
и  ;
;  . (1.3.18)
. (1.3.18) , (1.3.19)
, (1.3.19) .
. ) воспользуемся уравнениями Максвелла, которые в данном случае составляют следующую систему уравнений:
) воспользуемся уравнениями Максвелла, которые в данном случае составляют следующую систему уравнений: ; 2.
; 2.  . (1.3.20)
. (1.3.20) (1.3.21)
(1.3.21)
 (1.3.22)
(1.3.22)
 связаны с составляющей
связаны с составляющей 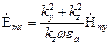 ;
; 
 ;
; 
 .
.


