
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоской волны, распространяющейся в однородной неограниченной среде
Пусть монохроматическая плоская волна распространяется в бесконечном пространстве, заполненном однородной средой, в направлении, заданном единичным вектором Любая составляющая вектора напряжённости поля плоской волны, движущейся в направлении
где Представим уравнение (1.2.1) в координатной форме. Для этого введём в рассмотрение следующие величины. Волновой вектор - вектор
где Радиус-вектор
Расстояние
Подставив (1.2.4) в (1.2.1), получим уравнение плоской волны, движущейся в направлении
Для дальнейшего анализа полезно отметить, что проекции волнового вектора
С учётом (1.2.7) уравнение (1.2.5) можно представить в следующих видах:
или
где
Проанализируем полученные уравнения плоской волны. Обратимся сначала к уравнению (1.2.8). В этом уравнении Приравняв фазу волны к постоянной величине, получим уравнение волновой поверхности:
Воспользовавшись выражением (1.2.9), можно представить уравнение волновой поверхности в координатной форме:
или
Из аналитической геометрии известно, что уравнение (1.2.13) является уравнением плоскости, перпендикулярной к вектору Предположим, что волна распространяется в среде без потерь и волновое число Рассмотрим теперь более общий случай, когда волновое число
где
С учётом (1.2.14) уравнение плоской волны (1.2.2) принимает следующий вид:
или
В выражениях (1.2.15) и (1.2.16) первый экспоненциальный множитель характеризует изменение амплитуды поля в пространстве, а второй является множителем бегущей волны. Направление вектора
или, с учётом (1.2.16),
Уравнение (1.2.17) является уравнением плоскости. Следовательно, волна, описываемая уравнениями (1.2.15) и (1.2.16), является плоской. Приравняв показатель первой экспоненты в (1.2.15) к постоянной величине, получим уравнение поверхности равных амплитуд
или, с учётом (1.2.16),
Из (1.2.18) следует, что поверхность равных амплитуд является плоской. Плоскости, описываемые уравнениями (1.2.17) и (1.2.18), совпадают или параллельны друг другу, т.е. векторы
В этом случае уравнение (1.2.15) описывает плоскую однородную волну, распространяющуюся в среде с потерями. При этом часть энергии волны расходуется на нагревание среды, и амплитуда волны по мере распространения уменьшается вдоль направления движения волны. В случае, когда условия (1.2.19) не выполняются, то есть плоскость равных амплитуд не параллельна плоскости равных фаз, уравнение (1.2.15) описывает один частный вид плоских неоднородных волн: волна распространяется в направлении, задаваемом вектором
|
||||||
|
Последнее изменение этой страницы: 2019-05-01; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.254.106 (0.007 с.) |
 . Вектор
. Вектор  ,
,  ,
,  (рис.1.1).
(рис.1.1). , описывается уравнением вида
, описывается уравнением вида (1.2.1)
(1.2.1) - расстояние от начала координат до волновой поверхности
- расстояние от начала координат до волновой поверхности  ;
;  - волновое число или коэффициент распространения волны в среде с абсолютной диэлектрической проницаемостью
- волновое число или коэффициент распространения волны в среде с абсолютной диэлектрической проницаемостью  и абсолютной магнитной проницаемостью
и абсолютной магнитной проницаемостью  .
. , направление которого совпадает с направлением распространения волны, а модуль равен волновому числу
, направление которого совпадает с направлением распространения волны, а модуль равен волновому числу  . В прямоугольной системе координат волновой вектор может быть представлен в следующей форме:
. В прямоугольной системе координат волновой вектор может быть представлен в следующей форме: , (1.2.2)
, (1.2.2) - проекции вектора
- проекции вектора  , проведённый из начала координат в произвольную точку волнового фронта:
, проведённый из начала координат в произвольную точку волнового фронта: (1.2.3)
(1.2.3) :
: (1.2.4)
(1.2.4)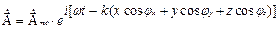 (1.2.5)
(1.2.5) связаны с модулем этого вектора следующими соотношениями:
связаны с модулем этого вектора следующими соотношениями: ; (1.2.6)
; (1.2.6) ;
;  ;
;  . (1.2.7)
. (1.2.7) , (1.2.8)
, (1.2.8) , (1.2.9)
, (1.2.9) , (1.2.10)
, (1.2.10) - начальная амплитуда поля, а
- начальная амплитуда поля, а  - начальная фаза поля.
- начальная фаза поля. - амплитудный множитель, зависящий от источника возбуждения плоской волны; множитель
- амплитудный множитель, зависящий от источника возбуждения плоской волны; множитель  - фазовый множитель или множитель бегущей волны. Фаза волны
- фазовый множитель или множитель бегущей волны. Фаза волны  зависит от времени и от пространственных координат.
зависит от времени и от пространственных координат. (1.2.11)
(1.2.11) (1.2.12)
(1.2.12) (1.2.13)
(1.2.13) , и, следовательно, к направлению распространения волны.
, и, следовательно, к направлению распространения волны. - действительная величина. В этом случае во всех точках плоскости, описываемой уравнением (1.2.13), амплитуда волны постоянна, т.е. поверхность равных фаз совпадает с поверхностью равных амплитуд. Это обстоятельство является, по определению, признаком плоской однородной волны.
- действительная величина. В этом случае во всех точках плоскости, описываемой уравнением (1.2.13), амплитуда волны постоянна, т.е. поверхность равных фаз совпадает с поверхностью равных амплитуд. Это обстоятельство является, по определению, признаком плоской однородной волны. является комплексной величиной. Представим волновой вектор
является комплексной величиной. Представим волновой вектор  в виде действительной и мнимой частей:
в виде действительной и мнимой частей: , (1.2.14)
, (1.2.14) ,
,
 (1.2.15)
(1.2.15) (1.2.16)
(1.2.16) совпадает с направлением распространения волны. Определим тип волны, описываемой уравнениями (1.2.15) и (1.2.16). Для этого запишем уравнение волнового фронта:
совпадает с направлением распространения волны. Определим тип волны, описываемой уравнениями (1.2.15) и (1.2.16). Для этого запишем уравнение волнового фронта: ,
,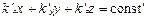 (1.2.17)
(1.2.17)
 (1.2.18)
(1.2.18) и
и  , перпендикулярные к этим плоскостям, коллинеарны, если в уравнениях (1.2.17) и (1.2.18) сохраняются постоянными отношения коэффициентов:
, перпендикулярные к этим плоскостям, коллинеарны, если в уравнениях (1.2.17) и (1.2.18) сохраняются постоянными отношения коэффициентов: (1.2.19)
(1.2.19)


