
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 1. Распознавание типов формальных языков и грамматикСтр 1 из 8Следующая ⇒
Лабораторная работа № 1. Распознавание типов формальных языков и грамматик Цель: -закрепить понятия « алфавит», «цепочка», «формальная грамматика» и «формальный язык», «выводимость цепочек», «эквивалентная грамматика»; - сформировать умения и навыки распознавания типов формальных языков и грамматик по классификации Хомского, построения эквивалентных грамматик. Основы теории Определение 1.1. Алфавитом V называется конечное множество символов. Определение 1.2. Цепочкой a в алфавите V называется любая конечная последовательность символов этого алфавита. Определение 1.3. Цепочка, которая не содержит ни одного символа, называется пустой цепочкой и обозначается e. Определение 1.4. Формальное определение цепочки символов в алфавите V: 1) e - цепочка в алфавите V; 2) если a - цепочка в алфавите V и а – символ этого алфавита, то aа – цепочка в алфавите V; 3) b - цепочка в алфавите V тогда и только тогда, когда она является таковой в силу утверждений 1) и 2). Определение 1.5. Длиной цепочки a называется число составляющих ее символов (обозначается | a |). Обозначим через V* множество, содержащее все цепочки в алфавите V, включая пустую цепочку e, а через V+ - множество, содержащее все цепочки в алфавите V, исключая пустую цепочку e. Пример 1.1. Пусть Определение 1.6. Формальной грамматикой называется четверка вида:
где VN - конечное множество нетерминальных символов грамматики (обычно прописные латинские буквы); VT - множество терминальных символов грамматики (обычно строчные латинские буквы, цифры, и т.п.), VT Ç VN =Æ; Р – множество правил вывода грамматики, являющееся конечным подмножеством множества (VT È VN) + ´(VT È VN) *; элемент (a, b) множества Р называется правилом вывода и записывается в виде a ® b (читается: «из цепочки a выводится цепочка b»); S - начальный символ грамматики, S Î VN. Для записи правил вывода с одинаковыми левыми частями вида Пример 1.2. Грамматика G 1 = ({0, 1}, { A, S }, P 1, S), где множество Р 1 состоит из правил вида: 1) S® 0 A 1;2)0 A® 00 A 1;3) A®e. Определение 1.7. Цепочка b Î (VT È VN) * непосредственно выводима из цепочки
Определение 1.8. Цепочка b Î (VT È VN) * выводима из цепочки Пример 1.3. В грамматике G 1 S Þ*000111, т.к. существует вывод Определение 1.9. Языком, порожденным грамматикой Пример 1.4. Для грамматики G 1 L (G 1) = {0 n 1 n | n> 0}. Определение 1.10. Цепочка Определение 1.11. Грамматики G 1 и G 2 называются эквивалентными, если Пример 1.5. Для грамматики G 1 эквивалентной будет грамматика G 2 = ({0, 1}, { S }, P 2, S), где множество правил вывода P 2 содержит правила вида S ® 0 S 1| 01. Рисунок 1.1 – Соотношение типов формальных языков и грамматик
Пример 1.6. Примеры различных типов формальных языков и грамматик по классификации Хомского. Терминалы будем обозначать строчными символами, нетерминалы – прописными буквами, начальный символ грамматики – S. а) Язык типа 0 L (G)={ 1) S ® aaCFD; 2) AD ® D; 3) F ® AFB | AB;4) Cb ® bC; 5) AB ® bBA;6) CB ® C; 7) Ab ® bA;8) bCD ® e.
б) Контекстно-зависимый язык L (G)={ anbncn | n ³1} определяется грамматикой с правилами вывода: 1) S ® aSBC | abc;2) bC ® bc; 3) CB ® BC;4) cC ® cc; 5) BB ® bb.
в) Контекстно-свободный язык L (G)={(ac) n (cb) n | n >0 } определяется грамматикой с правилами вывода: 1) S ® aQb | accb; 2) Q ® cSc.
г) Регулярный язык L (G)={ w ^ | w Î{ a, b }+, где нет двух рядом стоящих а } определяется грамматикой с правилами вывода: 1) S ® A ^ | B ^; 2) A ® a | Ba; 3) B ® b | Bb | Ab.
Постановка задачи к лабораторной работе № 1 При выполнении лабораторной работы следует реализовать следующие действия: 1) составить грамматику, порождающую формальный язык, заданный в соответствии с вариантом; 2) определить тип формальной грамматики и языка по классификации Хомского; 3) разработать программное средство, распознающее тип введенной пользователем грамматики по классификации Хомского. Варианты индивидуальных заданий представлены в таблице 1.1.
Таблица 1.1 – Варианты индивидуальных заданий к лабораторной работе № 1
Основы теории Распознавателем для регулярной грамматики является конечный автомат (КА). Определение 2.1. Детерминированным конечным автоматом (ДКА) называется пятерка объектов:
где Q - конечное множество состояний автомата; T - конечное множество допустимых входных символов; F - функция переходов, отображающая множество Q ´ T во множество Q; H - конечное множество начальных состояний автомата; Z - множество заключительных состояний автомата, Z Í Q. Определение 2.2. Недетерминированным конечным автоматом (НКА) называется конечный автомат, в котором в качестве функции переходов используется отображение
Основы теории Конечный автомат может содержать лишние состояния двух типов: недостижимые и эквивалентные состояния. Определение 3.1. Два различных состояния Определение 3.2. Состояние q КА называется недостижимым, если к нему нет пути из начального состояния автомата. Определение 3.3. КА, не содержащий недостижимых и эквивалентных состояний, называется приведенным или минимальным КА. Основы теории Определение 4.1. КС-грамматика называется приведенной, если она не имеет циклов, e-правил и бесполезных символов. Рассмотрим основные алгоритмы приведения КС-грамматик. Перед всеми другими исследованиями и преобразованиями КС-грамматик выполняется проверка существования языка грамматики.
Терминальных строк
Вход: КС-грамматика Выход: КС-грамматика
Шаг 1. Определить множество нетерминалов, порождающих терминальные строки, с помощью алгоритма 4.1. Шаг 2. Вычислить Пример 4.2. Дана грамматика Преобразуем ее в эквивалентную грамматику N 0 = Ø; N 1 = { S, B, C }; N 2 = { S, B, C }. Т.к. N 1= N 2, то N = { S, B, C }. После удаления бесполезных нетерминалов и правил вывода, получим грамматику
Основы теории Определение 6.1. КС-грамматика обладает свойством LL (k) для некоторого k >0, если на каждом шаге вывода для однозначного выбора очередной альтернативы МП-автомату достаточно знать символ на верхушке стека и рассмотреть первые k символов от текущего положения считывающей головки во входной строке. Определение 6.2. КС-грамматика называется LL (k) - грамматикой, если она обладает свойством LL (k) для некоторого k >0.
В основе распознавателя LL (k) - грамматик лежит левосторонний разбор строки языка. Исходной сентенциальной формой является начальный символ грамматики, а целевой – заданная строка языка. На каждом шаге разбора правило грамматики применяется к самому левому нетерминалу сентенции. Данный процесс соответствует построению дерева разбора цепочки сверху вниз (от корня к листьям). Отсюда и произошла аббревиатура LL (k): первая «L» (от слова «left») означает левосторонний ввод исходной цепочки символов, вторая «L» - левосторонний вывод в процессе работы распознавателя. Определение 6.3. Для построения распознавателей для LL (k) - грамматик используются два множества: - FIRST (k, a) – множество терминальных цепочек, выводимых из цепочки a Î(VT È VN)*, укороченных до k символов; - FOLLOW (k, A) – множество укороченных до k символов терминальных цепочек, которые могут следовать непосредственно за A Î VN в цепочках вывода. Формально эти множества можно определить следующим образом: - FIRST (k, a) = { w Î VT* | $ вывод a Þ* w и | w | £ k или $ вывод a Þ* wx и | w | = k; x, a Î (VT È VN)*, k > 0}; - FOLLOW (k, A) = { w Î VT * | $ вывод S Þ* aAg и w Î FIRST (k, g); a, g Î V*, A Î VN, k >0}.
Теорема 6.1. Необходимое и достаточное условие LL (1) - грамматики Для того чтобы грамматика G (VN, VT, P, S) была LL (1) - грамматикой необходимо и достаточно, чтобы для каждого символа А Î VN, у которого в грамматике существует более одного правила вида А ®a1 | a2 |…| a n, выполнялось требование:
FIRST (1, a iFOLLOW (1, A)) Ç FIRST (1, a jFOLLOW (1, A)) = Æ, " i ¹ j,0< i £ n, 0< j £ n.
Т.е. если для символа А отсутствует правило вида А ®e, то все множества FIRST (1, a1), FIRST (1, a2),…, FIRST (1, a n) должны попарно не пересекаться, если же присутствует правило А ®e, то они не должны также пересекаться с множеством FOLLOW (1, A). Для построения распознавателей для LL (1) - грамматик необходимо построить множества FIRST (1, x) и FOLLOW (1, A). Причем, если строка х будет начинаться с терминального символа а, то FIRST (1, x)= a, и если она будет начинаться с нетерминального символа А, то FIRST (1, x)= FIRST (1, A). Следовательно, достаточно рассмотреть алгоритмы построения множеств FIRST (1, A) и FOLLOW (1, A) для каждого нетерминального символа А. Алгоритм 6.1. Построение множества FIRST (1, A)
Для выполнения алгоритма необходимо предварительно преобразовать исходную грамматику G в грамматику G ¢, не содержащую e-правил (см. лабораторную работу № 4). Алгоритм построения множества FIRST (1, A) использует грамматику G ¢.
Шаг 1. Первоначально внести во множество первых символов для каждого нетерминального символа А все символы, стоящие в начале правых частей правил для этого нетерминала, т.е.
" А Î VN FIRST 0(1, A) = { X | A ® X a Î P, X Î(VT È VN),aÎ(VT È VN)*}.
Шаг 2.Для всех А Î VN положить: FIRSTi +1(1, A) = FIRSTi (1, A) È FIRSTi (1, B), " В Î(FIRST (1, A)Ç VN).
Шаг 3. Если существует А Î VN, такой что FIRSTi +1(1, A) ¹ FIRSTi (1, A), то присвоить i = i +1 и вернуться к шагу 2, иначе перейти к шагу 4. Шаг 4.Исключить из построенных множеств все нетерминальные символы, т.е.
" A Î VN FIRST (1, A) = FIRSTi (1, A) \ N .
Алгоритм 6.2. Построение множества FOLLOW (1, A)
Алгоритм основан на использовании правил вывода грамматики G. Шаг 1.Первоначально внести во множество последующих символов для каждого нетерминального символа А все символы, которые в правых частях правил вывода встречаются непосредственно за символом А, т.е. " A Î VN FOLLOW 0(1, A) = { X | $ B ® a AX b Î P, B Î VN, X Î (VT È VN), a, b Î(VT È VN)*}.
Шаг 2.Внести пустую строку во множество FOLLOW (1, S), т.е.
FOLLOW (1, S) = FOLLOW (1, S)È{ e }.
Шаг 3.Для всех А Î VN вычислить: FOLLOW ¢ i (1, A)= FOLLOWi (1, A)È FIRST (1, B)," B Î(FOLLOWi (1, A)Ç VN).
Шаг 4.Для всех А Î VN положить: FOLLOW²i (1, A)= FOLLOW¢i (1, A)È FOLLOW¢i (1, B), " B Î(FOLLOW¢i (1, A)Ç VN), если $ правило B ®e.
Шаг 5.Для всех А Î VN определить: FOLLOWi +1(1, A) = FOLLOW²i (1, A)È FOLLOW²i (1, B), для всех нетерминальных символов BÎVN, имеющих правило вида B ® aA, a Î(VT È VN)*.
Шаг 6.Если существует A Î VN такой, что FOLLOWi +1(1, A)¹ FOLLOWi (1, A), то положить i:= i +1 и вернуться к шагу 3, иначе перейти к шагу 7. Шаг 7.Исключить из построенных множеств все нетерминальные символы, т.е. " A Î VN FOLLOW (1, A) = FOLLOWi (1, A)\ N .
Основы теории
Определение 7.1. Приведенная КС-грамматика G (VN, VT, P, S) называется грамматикой простого предшествования, если выполняются следующие условия. 1) Для каждой упорядоченной пары терминальных и нетерминальных символов выполняется не более чем одно из трех отношений предшествования: а) Bi =× Bj (" Bi, Bj Î V), если и только если существует правило A ® xBiBjy Î P, где x, y Î V *; б) Bi <× Bj (" Bi, Bj Î V), если и только если существует правило A ® xBiDy Î P и вывод D Þ* Bjz, где A, D Î VN, x, y, z Î V *; в) Bi ×> Bj (" Bi, Bj Î V), если и только если существует правило A ® xCBjy и вывод С Þ* zBi или существует правило A ® xCDy Î P и вывод С Þ* zBi и D Þ* Bjw, где A, C, D Î VN, x, y, z, w Î V *. 2) Различные правила в грамматике имеют разные правые части. Определение 7.2. Отношения =×, <×, ×> называют отношениями простого предшествования для символов грамматики. В основе распознавателя для грамматик простого предшествования лежит правосторонний разбор строки языка. Исходной сентенциальной формой является заданная строка языка, а целевой – начальный символ грамматики. На каждом шаге разбора в исходной цепочке символов пытаются выделить подцепочку, совпадающую с правой частью некоторого правила вывода грамматики, и заменить ее нетерминалом, стоящим в левой части этого правила. Данная операция называется сверткой к нетерминалу, а заменяемая подстрока – основой сентенции. Описанный процесс разбора соответствует построению дерева вывода цепочки снизу вверх (от листьев к корню).
Метод предшествования основан на том факте, что отношения между двумя соседними символами распознаваемой строки соответствуют трем следующим вариантам:
- Bi = × Bi +1, если символы Bi и Bi +1 принадлежат основе; - Bi < × Bi +1, если Bi +1 – крайний левый символ некоторой основы; - Bi ×> Bi +1, если Bi – крайний правый символ некоторой основы.
Простого предшествования
Шаг 1. Поместить в верхушку стека символ ^н, считывающую головку – в начало входной цепочки символов. Шаг 2. До тех пор, пока не будет обнаружена ошибка, либо успешно завершен алгоритм разбора, сравниваем отношение простого предшествования символа на верхушке стека и очередного символа входной строки. При этом возможны следующие ситуации: - если самый верхний символ стека имеет меньшее или равное предшествование, чем очередной символ входной строки, то производим операцию «сдвиг» (перенос текущего символа из входной цепочки в стек и перемещение считывающей головки на один символ вправо); - если самый верхний символ стека имеет большее предшествование, чем очередной символ входной строки, то выполняем операцию «свертка». Для этого находим на верхушке стека «основу» сентенции, т.е. все символы, имеющие равное предшествование или один символ на верхушке стека. Символы основы удаляем из стека, выбираем правило вывода грамматики, имеющее правую часть, совпадающую с основой, и помещаем в стек левую часть выбранного правила. Если такого правила вывода найти не удалось, то выдается сообщение об ошибке, и разбор завершен неудачно; - если не установлено ни одно отношение предшествования между текущим символом входной цепочки и самым верхним символом в стеке, то алгоритм прерывается сообщением об ошибке; - если в стеке остаются символы ^н S, а во входном буфере только символ ^к, то входная строка прочитана полностью, и алгоритм разбора завершен успешно.
Пример 7.1. Дана грамматика G ({ a, (,)}, { S, R }, P, S), с правилами P: 1) S ®(R | a; 2) R ® Sa). Построить распознаватель для строки (((aa) a) a)^к.
Этап 1. Построим множества крайних левых и крайних правых символов L (A) и R (A) относительно всех нетерминальных символов грамматики (таблица 7.1).
Таблица 7.1 – Построение множеств L (A) и R (A) для грамматики G
Этап 2. На основе построенных множеств и правил вывода грамматики составим матрицу предшествования символов (таблица 7.2). Поясним заполнение матрицы предшествования. В правиле грамматики S ®(R символ (стоит слева от нетерминального символа R. Во множестве L (R) входят символы S, (, a. Ставим знак <× в клетках матрицы, соответствующих этим символам, в строке для символа (. В правиле грамматики R ® Sa) символ a стоит справа от нетерминального символа S. Во множество R (S) входят символы R, a,). Ставим знак ×> в клетках матрицы, соответствующих этим символам, в столбце для символа a. В строке символа ^н ставим знак <× в клетках символов, входящих во множество L (S), т.е. символов (, a. В столбце символа ^к ставим знак ×> в клетках, входящих во множество R (S), т.е. символов R, a,). В клетках, соответствующих строке символа S и столбцу символа a, ставим знак =×, т.к. существует правило R ® Sa), в котором эти символы стоят рядом. По тем же соображениям ставим знак =× в клетках строки а и столбца), а также строки (и столбца R.
Таблица 7.2 – Матрица предшествования символов грамматики
Шаг 3. Функционирование распознавателя для цепочки (((aa)a)a) показано в таблице 7.3.
Таблица 7.3 – Алгоритм работы распознавателя цепочки (((aa) a) a)
Шаг 4. Получили следующую цепочку вывода:
S Þ(R Þ(Sa)Þ((Ra)Þ((Sa) a)Þ(((Ra) a)Þ(((Sa) a) a)Þ(((aa) a) a).
Восходящее дерево вывода цепочки представлено на рисунке 7.2.
Рисунок 7.2 – Дерево вывода для цепочки (((aa) a) a) в грамматике G Лабораторная работа № 2. Постановка задачи Дана регулярная грамматика G = ({ A, B, C, S }, { a, b }, P, S), где Р: 1) S ® aB | aA; 2) A ® aA | bC | b; 3) B ® bB | aC | a.
Разработать программное средство, реализующее следующие функции: 1) ввод произвольной формальной грамматики с клавиатуры и проверка ее на принадлежность к классу регулярных грамматик; 2) построение по заданной регулярной грамматике конечного автомата; 3) преобразование недетерминированного конечного автомата к детерминированному конечному автомату; 4) вывод графа результирующего конечного автомата на экран.
Определение 1. Детерминированным конечным автоматом (ДКА) называется пятерка объектов:
где
Z - множество заключительных состояний автомата, Z Í Q. Определение 2. Недетерминированным конечным автоматом (НКА) называется конечный автомат, в котором в качестве функции переходов используется отображение
Приложение А (обязательное) Контрольный пример Исходная регулярная грамматика и соответствующий ей недетерминированный конечный автомат представлены на рисунке А.1.
Р
Рисунок А.1 – Исходная КС-грамматика и НКА 
Результирующий детерминированный конечный автомат, построенный по заданному недетерминированному конечному автомату, представлен на рисунке А.2.
Рисунок А.2 – Результирующий ДКА
(обязательное) Текст программы
Unit2.h
#include <fstream.h> #include <math.h> #include <sysutils.hpp> #include <graphics.hpp> #include <grids.hpp> #include <map> #include <set> #include <string> #include <list> #include <vector>
using std::string; using std::map; using std::multimap; using std::set; using std::pair;
// компаратор для работы в отображениях struct rulecmp{ bool operator()(const char c1, const char c2){ return (c1 < c2); } };
typedef string rule_r; typedef char rule_l; typedef pair<rule_l, rule_r> rule; typedef multimap<rule_l, rule_r, rulecmp> rulemap; typedef set<char> charset;
// класс грамматики class Grammar{ public: charset N; // мн-во нетерминалов charset T; // множество терминалов rulemap P; // множество правил char S; // начальный символ int IsRegular(); // проверка грамматики на регулярность void InGrammar(char *fname); // ввод грамматики из файла string AsString(); // вывод грамматики в строку void OutGrammar(char *fname); // вывод грамматики в файл };
typedef map<char, map<char, charset> > ftable;
// класс конечного автомата class FAutomat{ public: Grammar *G; // связанная грамматика charset Q; // множество состояний charset T; // множество входных символов ftable F; // таблица правил char H; // начальное состояние charset Z; // множество конечных состояний int MustPaint; // флаг отрисовки графа FAutomat(){ MustPaint = 0; } void SetGrammar(Grammar *NG); // связывание с грамматикой void CreateAutomat(); // создание автомата из грамматики void PaintAutomat(TCanvas * Canvas, long w, long h); // отрисовка графа void OutToTable(TStringGrid * Grid); // вывод таблицы правил в StringGrid void CreateDeterm(); // преобразование в ДКА };
Unit2.cpp
#include "Unit2.h"
int Grammar::IsRegular(){ if (N.empty() || P.empty()) return 0; for(rulemap::iterator i = P.begin(); i!= P.end(); i++){ if (!N.count(i->first)) return 0; //по длине правой части switch(i->second.length()){ case 1:{ if (!T.count(i->second[0])) return 0; break; } case 2:{ if (!T.count(i->second[0]) ||!N.count(i->second[1])) return 0; break; } default: return 0; } } return 1; }
void Grammar::InGrammar(char *fname){ long n, i; rule r;
ifstream fi(fname); N.clear(); T.clear(); P.clear(); // ввод нетерминалов fi >> n; for (i = 0; i < n; i++){ fi >> c; N.insert(c); } // ввод терминалов fi >> n; for (i = 0; i < n; i++){ fi >> c; T.insert(c); } // ввод правил fi >> n; for (i = 0; i < n; i++){ fi >> r.first >> r.second; P.insert(r); } // начальный символ fi >> S; }
string Grammar::AsString(){ string res = ""; charset::iterator i; res += "Nonterminals ("; res += IntToStr(N.size()).c_str(); res += "): "; for (i = N.begin(); i!= N.end(); i++){ res += *i; res += " "; } res += "\nTerminals ("; res += IntToStr(T.size()).c_str(); res += "): "; for (i = T.begin(); i!= T.end(); i++){ res += *i; res += " "; } res += "\nRules ("; res += IntToStr(P.size()).c_str(); res += ")\n"; for (rulemap::iterator j = P.begin(); j!= P.end(); j++){ res += "\t"; res += j->first; res += " -> " + j->second + "\n"; }
res += "Starting symbol: "; res += S; res += "\n"; return res; }
void Grammar::OutGrammar(char *fname){ ofstream fo(fname); charset::iterator i; fo << N.size() << "\n"; for (i = N.begin(); i!= N.end(); i++) fo << *i; fo << "\n" << T.size() << "\n"; for (i = T.begin(); i!= T.end(); i++) fo << *i; fo << "\n" << P.size() << "\n"; for (rulemap::iterator j = P.begin(); j!= P.end(); j++) fo << j->first << " " << j->second << "\n"; fo << "\n" << S; }
void FAutomat::SetGrammar(Grammar *NG){ G = NG; }
void FAutomat::CreateAutomat(){ rulemap::iterator i, j; rule r; char c, t; int k; // поиск незанятого символа for(c = 'A'; G->N.count(c); c++); // поиск правил вида A -> a без A -> aB for(i = G->P.begin(); i!= G->P.end(); i++) if (i->second.length() == 1 && G->T.count(i->second[0])){ for(j = G->P.lower_bound(i->first), k = G->P.count(i->first); k; j++, k--) if (j->second.length() == 2 && j->second[0] == i->second[0] && G->N.count(j->second[1])) break; if (!k){ // добавление правила вида A -> aC r.first = i->first; r.second = i->second + c; G->P.insert(r); G->N.insert(c); } } // начальный символ H = G->S; // состояния Q = G->N;
Лабораторная работа № 1. Распознавание типов формальных языков и грамматик Цель: -закрепить понятия « алфавит», «цепочка», «формальная грамматика» и «формальный язык», «выводимость цепочек», «эквивалентная грамматика»; - сформировать умения и навыки распознавания типов формальных языков и грамматик по классификации Хомского, построения эквивалентных грамматик. Основы теории Определение 1.1. Алфавитом V называется конечное множество символов. Определение 1.2. Цепочкой a в алфавите V называется любая конечная последовательность символов этого алфавита. Определение 1.3. Цепочка, которая не содержит ни одного символа, называется пустой цепочкой и обозначается e. Определение 1.4. Формальное определение цепочки символов в алфавите V: 1) e - цепочка в алфавите V; 2) если a - цепочка в алфавите V и а – символ этого алфавита, то aа – цепочка в алфавите V; 3) b - цепочка в алфавите V тогда и только тогда, когда она является таковой в силу утверждений 1) и 2). Определение 1.5. Длиной цепочки a называется число составляющих ее символов (обозначается | a |). Обозначим через V* множество, содержащее все цепочки в алфавите V, включая пустую цепочку e, а через V+ - множество, содержащее все цепочки в алфавите V, исключая пустую цепочку e.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.230 (0.517 с.) |
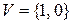 , тогда
, тогда  , а
, а  .
.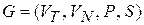 , (1.1)
, (1.1) используется сокращенная форма записи
используется сокращенная форма записи  .
. в грамматике
в грамматике  и
и  , где
, где  ,
,  и правило вывода
и правило вывода  содержится во множестве Р.
содержится во множестве Р. (n³0) такая, что
(n³0) такая, что 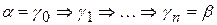 .
.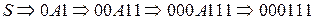 .
. .
. , для которой существует вывод S Þ* a, называется сентенциальной формой в грамматике
, для которой существует вывод S Þ* a, называется сентенциальной формой в грамматике 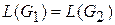 .
. } определяется грамматикой с правилами вывода:
} определяется грамматикой с правилами вывода: , (2.1)
, (2.1) во множество всех подмножеств множества состояний автомата
во множество всех подмножеств множества состояний автомата  , т.е. функция переходов неоднозначна, так как текущей паре
, т.е. функция переходов неоднозначна, так как текущей паре  соответствует множество очередных состояний автомата
соответствует множество очередных состояний автомата  .
. и
и  в конечном автомате
в конечном автомате  называются n -эквивалентными, n Î N È{0}, если, находясь в одном их этих состояний и получив на вход любую цепочку символов w: w Î VT*, |w| £ n, автомат может перейти в одно и то же множество конечных состояний.
называются n -эквивалентными, n Î N È{0}, если, находясь в одном их этих состояний и получив на вход любую цепочку символов w: w Î VT*, |w| £ n, автомат может перейти в одно и то же множество конечных состояний. .
. , такая, что
, такая, что 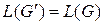 и для всех
и для всех 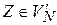 существуют выводы
существуют выводы  , где
, где  .
. , где
, где  - это множество правил, содержащих бесполезные нетерминалы
- это множество правил, содержащих бесполезные нетерминалы  .
.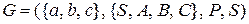 с правилами
с правилами 

 по алгоритму 4.2:
по алгоритму 4.2: с правилами
с правилами 


 3 Формальная модель задачи
3 Формальная модель задачи - конечное множество состояний автомата;
- конечное множество состояний автомата; - конечное множество допустимых входных символов;
- конечное множество допустимых входных символов; - функция переходов, отображающая множество Q´T во множество Q;
- функция переходов, отображающая множество Q´T во множество Q; - конечное множество начальных состояний автомата;
- конечное множество начальных состояний автомата; во множество всех подмножеств множества состояний автомата
во множество всех подмножеств множества состояний автомата  , т.е. функция переходов неоднозначна, так как текущей паре
, т.е. функция переходов неоднозначна, так как текущей паре  .
.





