
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замкнутость и полнота ортонормированных систем.
Опр. Система ф-ций {jn} из R([a;b]) наз-ся замкнутой в R([a;b]),если "fÎR([a;b]),"e>0 существует линейная комбинация Т1. Если {fn}-замкнутая ортонормированная система ф-ций в R([a;b]),то ряд Ф любой ф-ции Î R([a;b])сход-ся в среднем квадратическом к самой ф-ции f,т.е. Д-во:Пусть e>0-производная фиксиров. Поскольку {jn}-замкнутая ортогональная система ф-и в R([a;b]) то (17)=>(15),(16) Отметим,что из сходимости ряда Ф в среднеквадр. не следует равномерная или поточная сходимость этого ряда Опр. Система ф-ций {jn}из R([a;b]) наз-ся полной если "fÎR([a;b]) с условием (f,jn)=0,n=1,2… выполняется рввенство ||f||=0 Т. Всякая замкнутая ортонормированная система ф-ций {jn} в R([a;b]) явл-ся полной в R([a;b]) Д. Пусть fÎR([a;b]), (f,jn)=0,n=1,2…тогда коэффициент Ф ф-ции f cn(f,jn)=0,n=1,2…Следовательно из равенства Парсеваля ||f||<0 => система полная
Сходимость в среднем квадратичном. Равенство Парсеваля.
45 Тригонометрический ряд Фурье. Интегральное представление его сумм. Последовательность функций 1,cosx,sinx,…,cosnx,sinnx -π≤x≤π (1).Называется тригонометрической системой и она является ортогональной. Опр:Ряд вида Определение:Тригонометрический ряд (2) коэффициенты которого определяются формулами (3) называется тригонометрическим рядом Фурье функции f,а числа a0,an,bnЄR, n=1,2….. называются тригонометрическими коэфициентами ряда Фурье функции f.f= Все члены ряда Фурье функции f являются 2 π-периодическими и удовлетворяют условию
Тригонометрическая система (1) не является ортонормированной, при её нормировании получим следующую ортонормированную систему функций -π≤x≤π (4). Коэфициенты функции fЄR[-π;π] по системе функций (4) имеют вид:
46) Сходимость тригонометрического ряда Фурье в точке. Опр.: Функция
Опр.: Непрерывная справа(слева) функция
Если ф-ция непрерывна как справа, так и слева и Опр.: Точка Составим вспомогательную ф-цию Лемма: Пусть
Доказательство: В силу аддитивности Интеграл 47) Теорема Фейера Теорема 5 (Фейера). Если функция f непрерывна на отрезке [—п,п] и принимает на его концах равные значения, то последовательность ее сумм Фейера сходится равномерно на этом отрезке к самой функции. Доказательство. Пусть функция f непрерывна на отрезке [ - п, п] и f(-п) = f(п). Продолжим ее 2п-периодически на всю числовую ось R. Оценим разность f (x) — Зафиксируем точку x? [ — п, п] и зададим произвольное
где δ> 0 выбрано так, что значение модуля непрерывности w(
Оставшиеся два интеграла оцениваются одинаковым способом: функция f ограничена на всей числовой прямой, т.е. существует такая постоянная M > 0, что для всех x? R имеет место неравенство |f(x)|<= M. Согласно следствию 2 из леммы 1, правая часть полученного неравенства стремится к нулю при n → Аналогично, для любого x?R и всех n > n0 имеем Из (4.16), (4.17), (4.18) и (4.19) для произвольного x? R и всех n > n0 имеем |f (x) —
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.218.254 (0.009 с.) |
 конечного числа ф-ций послед.{jk},такая что ||(f-p)||< e. Следующее свойство ряда Ф запишем виде теоремы:
конечного числа ф-ций послед.{jk},такая что ||(f-p)||< e. Следующее свойство ряда Ф запишем виде теоремы: (15)при этом
(15)при этом  (р-во Парсеваля)(16)
(р-во Парсеваля)(16)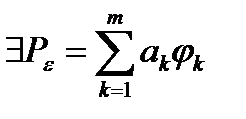 ,что ||(f-pe)||<e.Когда,учитывая
,что ||(f-pe)||<e.Когда,учитывая  и
и  получим,что"n³m
получим,что"n³m 
 (17)
(17)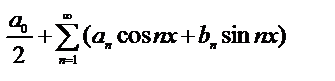 (2), где a0,an,bnЄR, n=1,2….. называются тригонометрическим рядом Фурье.коэфициенты Фурье функции fЄR[-π; π] относительно тригонометрической системы функций (1) определяется формулами
(2), где a0,an,bnЄR, n=1,2….. называются тригонометрическим рядом Фурье.коэфициенты Фурье функции fЄR[-π; π] относительно тригонометрической системы функций (1) определяется формулами 
 , n=1,2…(3)
, n=1,2…(3)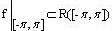 , через Rb обозначим множество всех функций f:R→R являющимися 2 π-периодическими
, через Rb обозначим множество всех функций f:R→R являющимися 2 π-периодическими 



 непрерывна в точке x справа(слева), если
непрерывна в точке x справа(слева), если 

 в точке х, то функция
в точке х, то функция  , причем
, причем 
 называется регулярной точкой функции
называется регулярной точкой функции 
 . Если ф-ция
. Если ф-ция 
 периодическая, абсолютно интегрируемая ф-ция на отрезке длины
периодическая, абсолютно интегрируемая ф-ция на отрезке длины  , где
, где  сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
 является сходящимся, т.к. ф-ция
является сходящимся, т.к. ф-ция  явл. абсолютно интегрируемой ф-цией как сумма абсолютно интегрируемых функций, а функция 1/(sin(t/2)) является непрерывной на отрезке [
явл. абсолютно интегрируемой ф-цией как сумма абсолютно интегрируемых функций, а функция 1/(sin(t/2)) является непрерывной на отрезке [  ].
]. (x)
(x) > 0. Имеем
> 0. Имеем (4.16)
(4.16)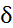 ; f) функции f удовлетворяет неравенству w(
; f) функции f удовлетворяет неравенству w( . Это возможно, так как функция f равномерно непрерывна на всей числовой оси R. Поэтому для любого x? R имеем
. Это возможно, так как функция f равномерно непрерывна на всей числовой оси R. Поэтому для любого x? R имеем . (4.17)
. (4.17) , поэтому существует такое n0, что при всех n > n0 выполняется неравенство
, поэтому существует такое n0, что при всех n > n0 выполняется неравенство  (4.18)
(4.18) (4.19)
(4.19) и, так как выбор номера n0 не зависит от выбора точки x, то последовательность {
и, так как выбор номера n0 не зависит от выбора точки x, то последовательность {  n(x)} сходится равномерно на всей
n(x)} сходится равномерно на всей


